LTV预估的一些思考

什么是LTV

用户生命周期价值(Lifetime Value, LTV)是一个非常重要的指标，定义为单个用户在某种生命周期内(i.e. 从开始使用产品到停止使用期间) 为产品创造的总价值。

比如GMV、XX日内产生的GMV。每个人或者公司对价值的定义不一样，传统市场下，LTV的定义为

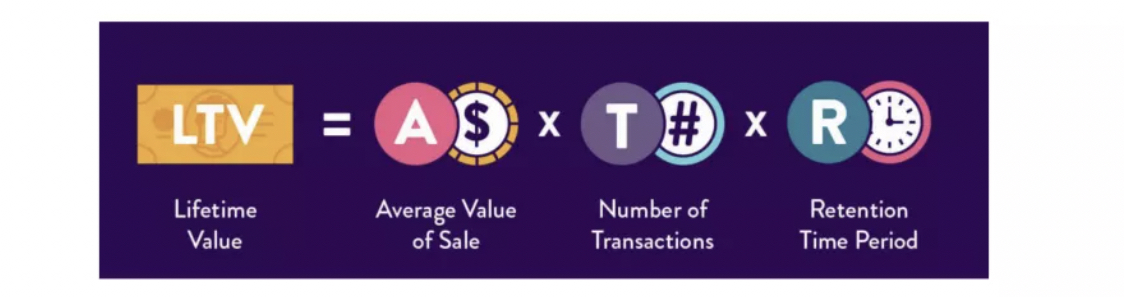
在传统的经济学、市场学当中，LTV经常会被应用的场景是：在一个超市中去分析来这个超市的人的整体的LTV，即LTV=Average Value of Sale *Number of Transactions * Retention Time Period，然后再做一个宏观的数据统计和预测。(ref: datafun&快手LTV )

LTV预估的价值和难点

LTV的价值之一是在做一些营销活动如拉新、召回或者广告投放中，如果提前知晓用户所能产生的潜在价值，那么将有限的资源倾斜到何处便有了一个指导。对应到本问题，就等于预测某个人在未来一段时间内的GMV、购买量或者其他你所定义的价值标准，一般来说，这是个回归问题。

那么预估LTV的核心难点在于：整个群体的数据分布中，混合了如：泊松、指数等多种分布，一般来说以以下形态展现

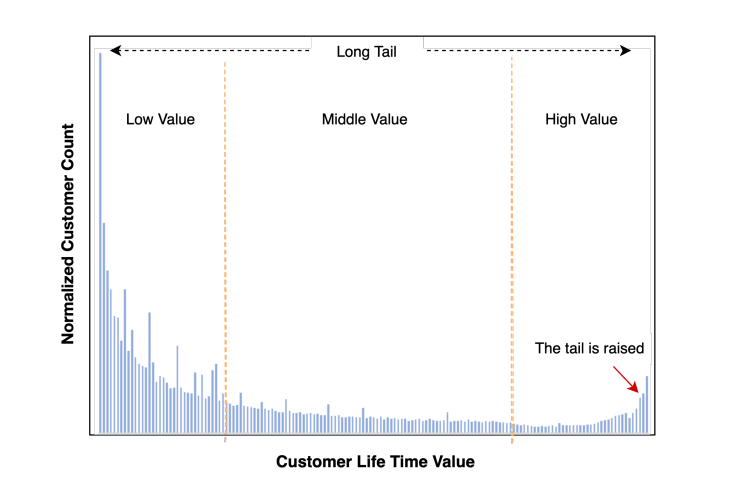
公司的实际数据不方便放，就放一张公开论文的图。大体意思都差不多。一般来说，尾部的峰值还会更高一些。

那么，出现这些分布可能得原因是：

• 1. 有部分人就是来玩的：一段时间内没有产生价值; 表现上就是0值部分很多。（这种0值比较多的回归问题也被称作0膨胀泊松分布问题）。
• 1. 有部分人来了就给你搞个大的：周期内贡献了很大价值，这部分人很少，但贡献了大部分收益。比如沉默了很久的淘宝用户突然上来买了个4090，或者打车来了个跨城。
• 1. 剩下就是大部分人，他们的价值和行为服从指数分布。

通常，LTV使用回归类建模，loss使用mse，而mse的特点恰好无法准确的处理好0膨胀问题，且对极值比较敏感。这些造成了LTV预估的困难。

有困难就要上，没有困难制造困难也要上，来总结一下实际生产中遇到的问题和解法。

LTV预估的方法

LTV的预估并非无迹可寻，一般来说，可以先使用比较强的Tree-based 模型做回归试试水，但不出意外的话，模型会被两端的分布带偏。

也可以尝试把目标进行拆解：0值部分使用一个交易达成率模型，其余部分正常使用回归模型，两个模型预测值相乘，表征了 交易达成率*达成价值。一般来说能缓解这个问题。

也可以针对性的使用一些深度的方法去拟合这类分布。下面做具体介绍。

模型如何评估

算法建模过程中，一个比较核心的问题是：找到一个合适的指标来表征你模型的效果，这个不仅关系到离线迭代的效率，更关系到离在线指标一致性的问题。

有可能离线指标很好，但是线上业务指标很拉胯。

那么，对于LTV回归类问题，我个人认为其实LTV是不可能做准的。连我自己都不知道我下一秒到底会不会消费，这时候用一些回归性的指标，比如r2之类的，可能就不太好，你会发现迭代了半天其实效果并不好。但是换个角度想，我更有可能知道A这个潜在的消费价值在B这个人之上，那么我的模型只要能够把A的LTV排在B的LTV之前就很可以了。

得益于AUC的灵感，我们可以把这个问题转化为一个 回归下的排序问题。

有没有类似AUC一样正对回归问题的排序指标呢？有，那就是累计增益分布曲线，也叫做GINI曲线, 曲线下的面积就是GINI指数， 面积大小关系的含义其实和AUC一样。

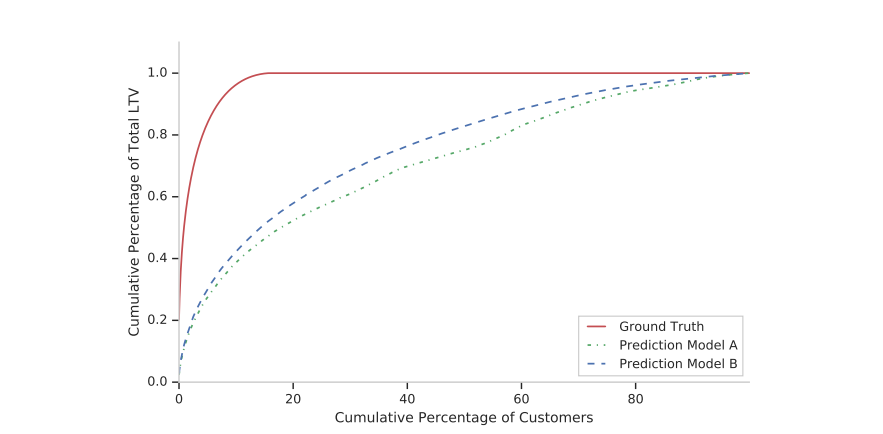
那么这样的曲线的画法如下：

假设存在一个3列的dataframe：[user_id, label, predictions]

1. 先根据label和prediction列，各自降序排序并等频分桶。

2. 统计 随机分桶(anchor，通常就是那根对角线)、labe分桶和prediction分桶内的价值和(就是列元素取值)。那么模型足够强的话，prediction列的桶会是单调的。随机桶通常每桶价值和事一样的。

3. 最开始的地方补一个0桶，取值为0，主要是为了画图好看

4. 分桶内gmv值累加：后一个桶累加前一个桶的值，即为累计值。

5. 对label和prediction，计算每桶的累计增益，以prediction列为例：

   • [桶内累计的价值 / 桶内人数] * 对应随机桶的人数，然后归一化(一般除以所有桶的最大值就行)。这一步的目的是计算相对于随机，模型能在人均粒度上带来多大的效果提升。
   • 桶内的人群价值增益 - 随机的人均价值增益 得到每桶的增益。这个值用来描曲线。

6. 根据每桶增益，画出累计增益曲线，得到的值就是曲线下方一下，anchor以上部分的面积。+0.5就是曲线下方的面积。

使用传统机器学习建模

这里以xgb为例，一般不拘泥于模型。

XGB or else

直接用xgb做回归的话，在这个问题上，不出意外的话，预估值会呈正态分布。简单来说就是头部和尾部都拟合不好，整体方差会比较低。

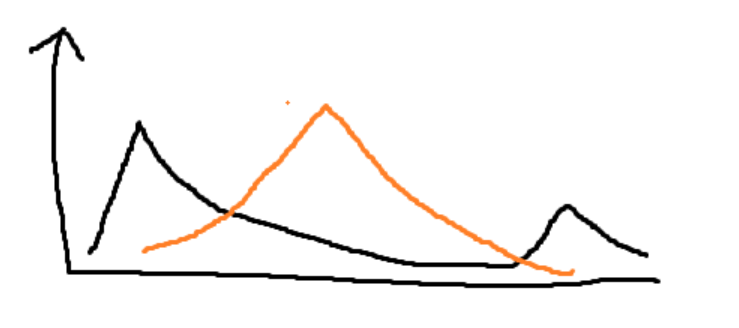
Two-Stage XGB

单纯的使用xgb会存在一个问题：分布拥挤，头尾的两个极值没有学到，进而导致整体预估的均值很高，方差很低(vs真实值)。因此，简单来说有2个思路可以实做一下：

1. LTV可以被认为有2部分组成：是否成交 * 成交价。在分布中，ltv=0的部分可以被认为没有成交成功，剩余部分为成交成功后的价值。因此训练一个成交率分类模型和一个价值模型:

\[\hat LTV=F_{deal}(X) * F_{regression}(X)
\]

1. 第二种是把分布拆解为2部分：2个峰值=0和>100(假设尾峰以100为界)为第一部分做一个二分类。剩余部分继续做回归。

但第二种相比于第一种，2个极值都需要预测很准才行。离线的gini系数来看，第1种效果是最好的，线上roi相对有大约4%的提升。

Weighted Two-Stage XGB

前文two-stage的模型在实际使用中，发现线上表现不是很稳定。表现之一是我们的LTV，这里是gmv，gmv掉了，但是roi是上涨的, roi=gmv/cost => gmv降低的幅度<cost降低的幅度。这时候我们分析了一下数据发现高价值部分成交量会不稳定。

于是，对于高价值部分我们选择加权，其次，xgb的loss选择了更合适的指数分布的 tweedie loss

事实证明该方案还是有效的，在线的roi相对涨了9%

对数正态参数估计

two-stage模型依然还是有他的弊端：

• 两个stage的模型是相互独立的，会存在误差累计。
• 数据分布包含了一个指数分布和一个极值，不符合树模型loss的假设。

因此我们需要找到一种方法，将two-stage变成end2end的one-stage模型，这方面，深度是最好的选择。这里分享一篇Google在做用户LTV预估方面的文章，来处理这种混合分布的概率估计算法：zero-inflated lognormal (0膨胀对数正态分布， ZILN)。

从实操上看，离线效果明显，分布也比较符合预期。

对数正态分布 (lognormal dist)

我们先了解一下对数正态分布, 简单的理解就是任意随机变量取对数后服从正态分布，则认为这个随机变量服从对数正态分布：

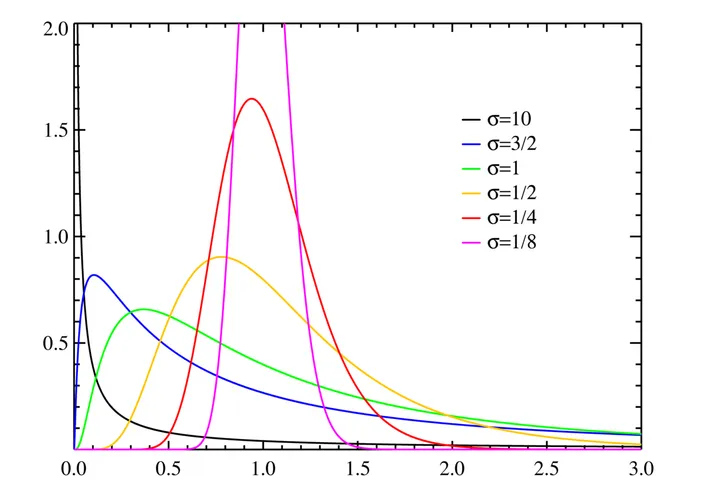
对数正态分布的概率密度函数为：

\[f(x; \mu, \sigma) = \frac{1}{x\sigma \sqrt{2\pi}} e^{-(\ln x - \mu)^2/2\sigma^2}, \quad\quad x>0
\]

其中,\(\mu\)和\(\sigma\) 分别是均值和标准差。该pdf的期望为：

\[E(X)=e^{\mu+\sigma^2/2}
\]

\[VAR(X)=(e^{\sigma^2}-1)e^{2\mu+\sigma^2}
\]

ZILN Loss

上面说的mse面临的一些问题，诸如无法准确的拟合0值，对高价值用户敏感，然而0膨胀的方式又比较麻烦，需要维护2个模型，容易造成误差累计，由此提出了对数正态参数估计模型

首先对概率密度取负对数简化计算:

\[L_{lognormal}(x; \mu,\sigma)=log(x\sigma\sqrt{2\pi})+\frac{(logx-\mu)^2}{2\sigma^2}
\]

这部分的参数会用于拟合指数分布部分，实操中，需要对label取个对数以满足正态分布的hyposis，对于0的部分，则用2分类交叉熵就ok了，那么我们就得到end2end的loss：

\[L_{ZILN}(x; \mu,\sigma)=-Sign_{\{x=0\}} log(1-p)-Sign_{\{x>0\}}(log p - L_{lognormal}(x; \mu,\sigma))
\]

\[L_{ZILN}(x; \mu,\sigma)=L_{CrossEntropy}(Sign_{\{x>0\}})+Sign_{\{x>0\}}L_{lognormal}(x; \mu,\sigma)
\]

其中，交叉熵部分表示是否为0。

如何估计pdf中的三个参数：\(p，\mu 和 \sigma\)

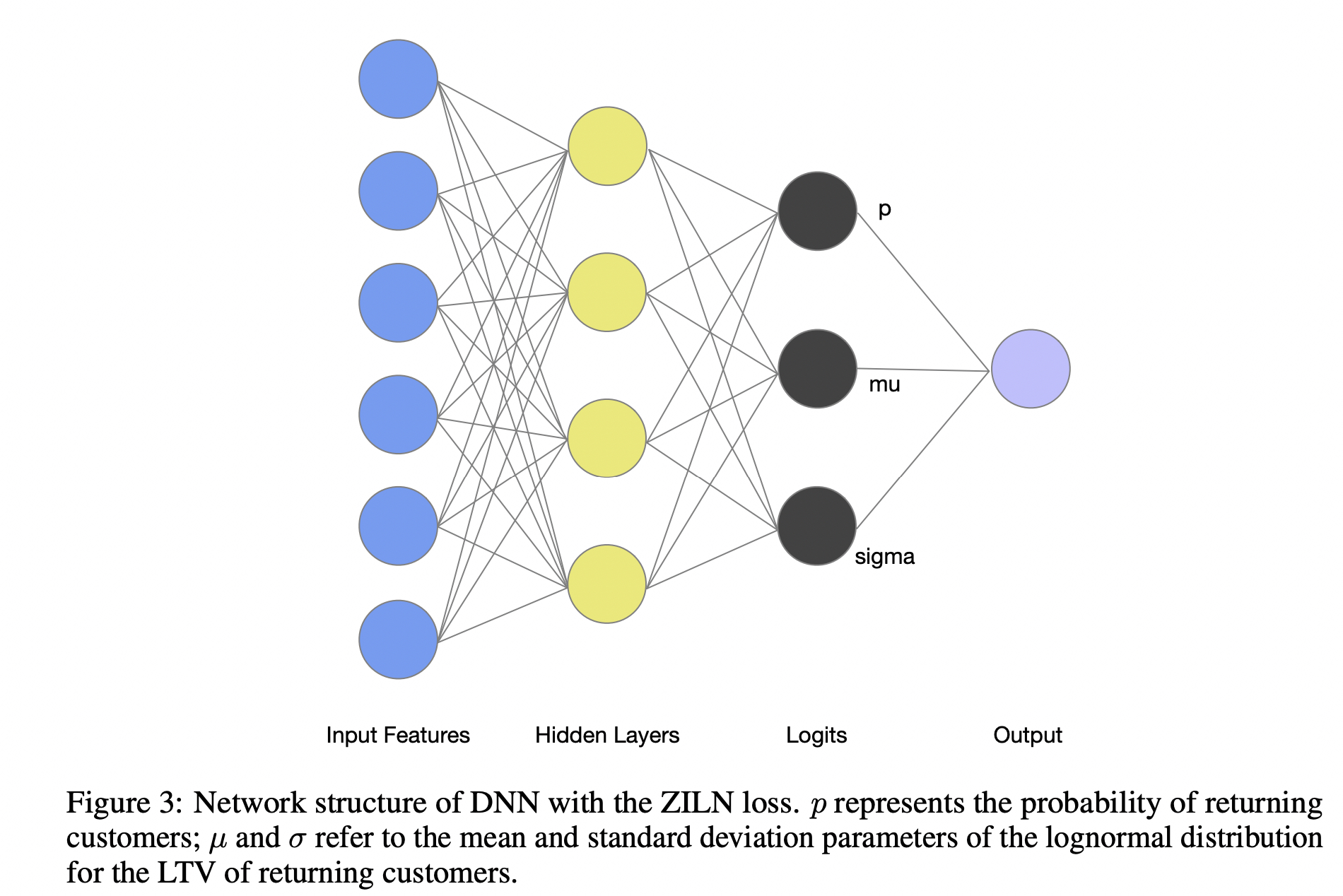
谷歌这里使用nn来预估三个值，其loss定义已推出，loss实现：

def zero_inflated_lognormal_loss(labels: tf.Tensor,
                                 logits: tf.Tensor) -> tf.Tensor:
  """Computes the zero inflated lognormal loss.

  Usage with tf.keras API:

  model = tf.keras.Model(inputs, outputs)
  model.compile('sgd', loss=zero_inflated_lognormal)

  Arguments:
    labels: True targets, tensor of shape [batch_size, 1].
    logits: Logits of output layer, tensor of shape [batch_size, 3].

  Returns:
    Zero inflated lognormal loss value.
  """
  labels = tf.convert_to_tensor(labels, dtype=tf.float32)
  positive = tf.cast(labels > 0, tf.float32)

  logits = tf.convert_to_tensor(logits, dtype=tf.float32)
  logits.shape.assert_is_compatible_with(
      tf.TensorShape(labels.shape[:-1].as_list() + [3]))

  positive_logits = logits[..., :1]
  classification_loss = tf.keras.losses.binary_crossentropy(
      y_true=positive, y_pred=positive_logits, from_logits=True)

  loc = logits[..., 1:2]
  scale = tf.math.maximum(
      tf.keras.backend.softplus(logits[..., 2:]),
      tf.math.sqrt(tf.keras.backend.epsilon()))
  safe_labels = positive * labels + (
      1 - positive) * tf.keras.backend.ones_like(labels)
  regression_loss = -tf.keras.backend.mean(
      positive * tfd.LogNormal(loc=loc, scale=scale).log_prob(safe_labels),
      axis=-1)

  return classification_loss + regression_loss

如何预测？

从loss可知模型在学3个参数：\(\mu, \sigma\) 和一个是否是0的概率\(p\)。 因此模型的预测结果会返回一个 batch_size * 3大小的mat。里面存储3个值。

那么当学习到\(\mu, \sigma\) 之后，可以利用上文概率密度函数带入参数得到结果：

\[\hat y = p * E(x)
\]

def zero_inflated_lognormal_pred(logits: tf.Tensor) -> tf.Tensor:
  """Calculates predicted mean of zero inflated lognormal logits.

  Arguments:
    logits: [batch_size, 3] tensor of logits.

  Returns:
    preds: [batch_size, 1] tensor of predicted mean.
  """
  logits = tf.convert_to_tensor(logits, dtype=tf.float32)
  positive_probs = tf.keras.backend.sigmoid(logits[..., :1])
  loc = logits[..., 1:2]
  scale = tf.keras.backend.softplus(logits[..., 2:])
  preds = (
      positive_probs *
      tf.keras.backend.exp(loc + 0.5 * tf.keras.backend.square(scale)))
  return preds

实际效果

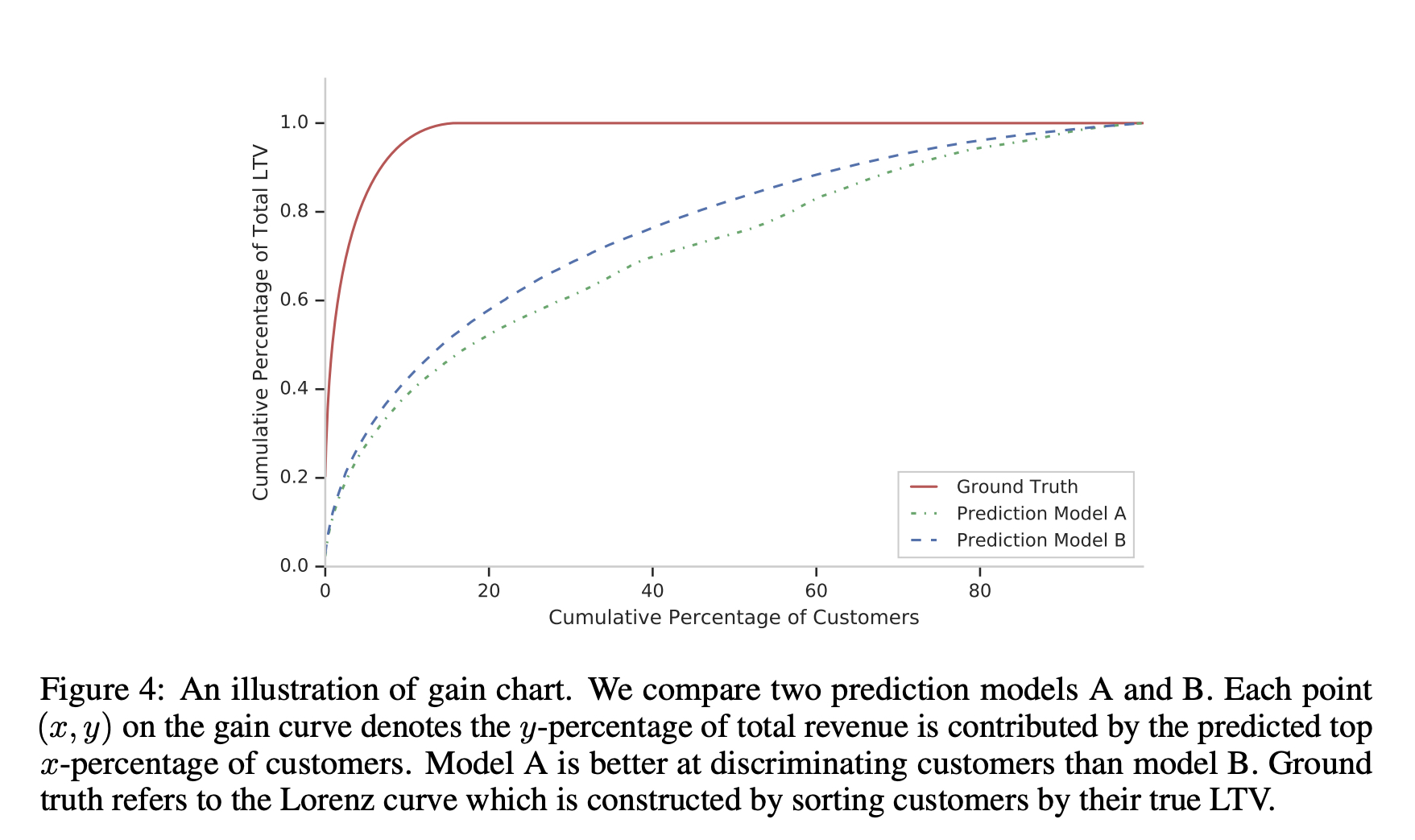
从累计增益曲线可以看到，ZILN的效果会优一些，该曲线可以理解为用于评价连续值上的排序能力，因为本身LTV的预估不可能精准

从中也可以观察到，大约20%的用户贡献了超80%的LTV，所以label曲线最上面是平的。

refs

[1] Billion-user Customer Lifetime Value Prediction: An Industrial-scale Solution from Kuaishou

[2] A DEEP PROBABILISTIC MODEL FOR CUSTOMER LIFETIME VALUE PREDICTION