FJ省队集训DAY4 T3

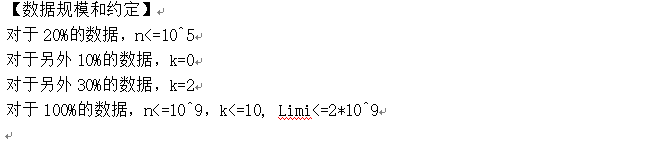
 #include<cstdio>
 #include<iostream>
 #include<cmath>
 #include<cstring>
 #include<algorithm>
 typedef long long ll;
 ll read(){
     ll t=,f=;char ch=getchar();
     while (ch<''||ch>''){if (ch=='-')f=-;ch=getchar();}
     while (''<=ch&&ch<=''){t=t*+ch-'';ch=getchar();}
     return t*f;
 }

 int n,K,lim,ans=;
 int a[],tot=,cnt[],C[][];
 ll pw_[],*pw;

 void dp(int id,bool f,bool f2) {
     if (id==) {
         ++ans;
         return;
     }
     if (f2) {
         for (int i=;i<=(f?:a[id]);i++)
             if (cnt[i]>) {
                 --cnt[i];
                 dp(id-,f|(i<a[id]),);
                 ++cnt[i];
             }
         return;
     }
     if (f) {
         int tmp=;
         for (int j=;j<=;j++)
             tmp*=C[id][cnt[j]],
             id-=cnt[j];
         ans+=tmp;
         return;
     }
     for (int i=;i<=a[id];i++)
         if (cnt[i]>) {
             --cnt[i];
             dp(id-,f|(i<a[id]),);
             ++cnt[i];
         }
 }
 void dfs(int num,int tot2,int used){
     if (num==){
         cnt[]=tot2-used;
         int p=-,g=;
         for (int i=;i<=&&p==-;g+=cnt[i++]){
             if (g<(tot2+)/&&g+cnt[i]>=(tot2+)/)
              p=i;
         }
         ll val=;
         for (int i=;i<=;i++)
          val+=cnt[i]*pw[i-p];
         if (val<=lim) dp(tot2,tot2<tot,);
         return;
     }
     for (int i=;i<=tot2-used;i++){
         cnt[num]=i;
         dfs(num+,tot2,used+i);
     }
 }
 void init(){
     pw=pw_+;
     for (int i=-;i<=;i++){
         pw[i]=;
         for (int j=;j<=K;j++)
          pw[i]*=i;
     }
     C[][]=;
     for (int i=;i<=;i++){
         C[i][]=;
         for (int j=;j<=i;j++)
          C[i][j]=C[i-][j]+C[i-][j-];
     }
 }
 int main(){
     n=read();K=read();lim=read();init();
     while (n){
         a[++tot]=n%;
         n/=;
     }
     for (int i=;i<=tot;i++) dfs(,i,);
     printf("%d\n",ans);
 }