poj3254Corn Fields题解

Corn Fields

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions: 9623		Accepted: 5092

Description

Farmer John has purchased a lush new rectangular pasture composed of M by N (1 ≤ M ≤ 12; 1 ≤ N ≤ 12) square parcels. He wants to grow some yummy corn for the cows on a number of squares. Regrettably, some of the squares are infertile and can't be planted. Canny FJ knows that the cows dislike eating close to each other, so when choosing which squares to plant, he avoids choosing squares that are adjacent; no two chosen squares share an edge. He has not yet made the final choice as to which squares to plant.

Being a very open-minded man, Farmer John wants to consider all possible options for how to choose the squares for planting. He is so open-minded that he considers choosing no squares as a valid option! Please help Farmer John determine the number of ways he can choose the squares to plant.

Input

Line 1: Two space-separated integers: M and N 
Lines 2..M+1: Line i+1 describes row i of the pasture with N space-separated integers indicating whether a square is fertile (1 for fertile, 0 for infertile)

Output

Line 1: One integer: the number of ways that FJ can choose the squares modulo 100,000,000.

Sample Input

2 3
1 1 1
0 1 0

Sample Output

9

Hint

Number the squares as follows:

1 2 3
  4  

There are four ways to plant only on one squares (1, 2, 3, or 4), three ways to plant on two squares (13, 14, or 34), 1 way to plant on three squares (134), and one way to plant on no squares. 4+3+1+1=9.

题目大意：

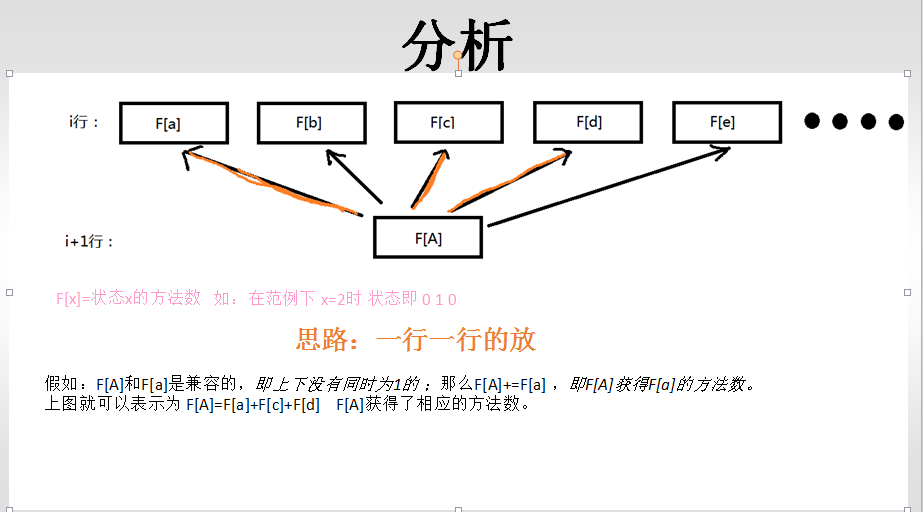
给你一个N*M的矩阵，矩阵里的元素由0和1组成，1代表肥沃的土地可以种草，0则不可以种草。如下： N=2 M=3 1 1 1 0 1 0 现有若干头牛，请将它们放入有草的地方吃草，注意上下左右不能相邻。 那么问题来了，请问有多少种放法？

分析：

 #include<iostream>
 #include<sstream>
 #include<stdio.h>
 #include<string>
 #include<string.h>
 #include<math.h>
 #include<time.h>
 #include<algorithm> 

 #define LEN 1000000
 #define INF 99999
 #define ALLSTATES 4096 //最大状态 

 using namespace std;

 int allstates=;
 int n,m;
 int F[][ALLSTATES]={};   //方法数
 int Matrix[][]={};//土地的样子

 bool andMatrix(int row,int states)//是否和土地兼容
 {
     for(int i=;i<=m;i++)
     {
         if(Matrix[row][i]==)//如果这里是空的 那么肯定不能放牛
         {
             if(states&(<<i-))
             {
                 return false;
             }
         }

     }
     return true;
 }

 bool linetest(int states)//判断行是否相邻
 {
     int i=;

     while(i<m)
     {
         if(states&(<<i))//如果是1 那么你的左边不应该是1
         {
             if(i+<m && states&(<<(i+))){    return false;        }//是1返回错误
              else{i+=;}//不是1 跳过一格
         }
         else{    i++;    }
     }
         return true;
 }

 bool upanddown(int upstates,int downstates)//判断上下是否相邻
 {
     int i=;

     while(i<m)
     {
         if(upstates&(<<i) && downstates&(<<i))
         {
             return false;
         }
         else
         {
             i++;
         }

     }
     return true;
 }

 int main()
 {
     //读入--------------------------------------------
     cin>>n>>m;
      //读入矩阵
     for(int i=;i<=n;i++)
       for(int j=;j<=m;j++)
       {
             cin>>Matrix[i][j];
       }
     //处理--------------------------------------------
     allstates=<<m;//m个格子的所有状态
 //    cout<<andMatrix(1,5)<<endl;
 //    cout<<linetest(5)<<endl;
     //cout<<allstates;
     //先处理第一行
     for(int j=;j<allstates;j++)//allstates为所有状态
     {
         if(andMatrix(,j) && linetest(j))//
         {
             F[][j]=;
         }
     }
     //cout<<allstates;
     //处理后面的行数
       for(int row=;row<=n;row++)
        for(int j=;j<allstates;j++)
        {
                if(andMatrix(row,j)== || !linetest(j))//如果j不符合土地直接跳过
             {
                 continue;
             }
         for(int k=;k<allstates;k++)
         {
             if(F[row-][k] && upanddown(j,k))
             {
                 F[row][j]+=F[row-][k];
             }
         }
       }
       //统计所有方法数
      int ct=;

      //for(int i=1;i<=n;i++)
 //     {
 //      for(int j=0;j<allstates;j++)
 //      {
 //          cout<<F[i][j];
 //      }
 //      cout<<endl;
 //     }
       //cout<<ct;
        for(int j=;j<allstates;j++)
        {
             ct+=F[n][j];
             ct%=;
        }
       cout<<ct;

     return ;
 }

2015-07-26 13:21:58