最快速的“高斯”模糊算法（附Android源码）

 

这是一个外国人的算法，本人是搬运工。参考：http://blog.ivank.net/fastest-gaussian-blur.html

 

1：高斯模糊算法（参考：http://www.ruanyifeng.com/blog/2012/11/gaussian_blur.html）

所谓的模糊算法就是当前像素点和周围像素点进行加权均值之后的结果替换当前像素值。因此均值模糊是最简单的，只要将周围的像素点相加取平均值即可。

    而高斯模糊则是将周围的像素点的权值按照高斯分布进行取值，即根据距离当前像素点的距离确定取值的权值。如下图：距离当前像素点越近权值越高，反之越低。之所以这么做是因为高斯模糊出来的效果比较好。

（图片来自：http://www.ruanyifeng.com/blog/2012/11/gaussian_blur.html）

 

2：高斯模糊的时间复杂度

    假设图片的像素宽，高是（w*h），模糊半径是r，那么二维的高斯模糊的时间复杂度是w*h*r*r，如果图片过大则时间复杂度很高（见二维的高斯分布）。而一般的解决办法就是将二维的变为一维，因为高斯分布支持卷积运算（参考：http://blog.csdn.net/liguan843607713/article/details/42215965），因此先进行x方向的一维的高斯模糊，在进行y轴方向的一维高斯模糊，这样做出来的效果是一样的（见一维的高斯分布）。

    但是即使这样高斯模糊的时间复杂度是w*h*2*r，仍然很高。所以需要另一种办法解决。

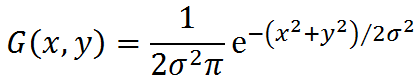
二维的高斯分布

 

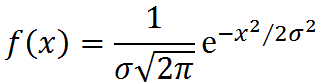
一维的高斯分布

 

3：最快速的高斯模糊

    其实这篇文章（http://blog.ivank.net/fastest-gaussian-blur.html）给出的并不是真正的高斯模糊，而是使用均值模糊（box blur）进行拟合之后，效果接近高斯模糊。均值模糊之所以快速是因为进行模糊处理时当前的像素值的计算可以利用到之前只算的值，所以不必重复计算。而均值模糊也可以进行卷积计算，可以讲二维的降为一维。因此大大减少了时间的消耗。

    根据这篇论文（http://www.csse.uwa.edu.au/~pk/research/pkpapers/FastGaussianSmoothing.pdf），基本上3次均值模糊就可以接近于高斯模糊（本人论文并没有研读，只是直接使用了http://blog.ivank.net/fastest-gaussian-blur.html给出的计算半径的公式）。问题的关键就在于怎么根据高斯模糊的半径，找到对应的均值模糊模糊的半径。上述网址给出了计算方法：

 

    总之，总结起来就是，利用多次均值模糊进行拟合成高斯模糊。一般来说3次就可以达到效果。因为均值模糊的时间复杂度是w*h，所以利用多次均值模糊代替高斯模糊的时间复杂度大大减少。具体效果参考http://blog.ivank.net/fastest-gaussian-blur.html。

 

4：说明

    在Android最快的高斯模糊并不是以上的两种方法，而是使用RenderScript，但是RenderScript的缺点是模糊半径不能大于25。在实际应用中可以先将图片缩小模糊，再放大可以节省很多时间。

 

5：Android源代码分享：

    Android代码包括，一个一维的标准的高斯模糊和利用3次均值模糊拟合过的"最快速高斯模糊"。利用jni编写。

 

代码Github网址：https://github.com/amazingyyc/fasted_gauss_blur

 

原始图片，670x455的分辨率

 

模糊后的效果：可以看到两个算法时间差别巨大！！