zoj3806Incircle and Circumcircle

链接

自己的本本没有装画图软件，先借用两张图片。。博客园不让贴源地址。。。

可以想到对于一个确定的外接圆的三角形来说内切圆最大的时候为等边三角形，如下图：

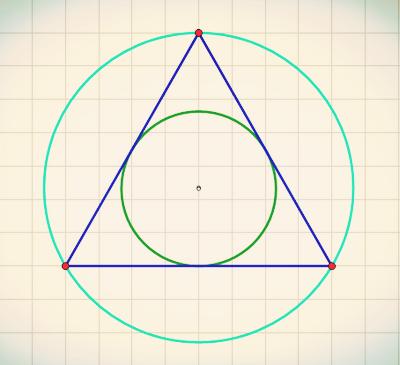
确定有合法的解之后，接下来就是去找这个解，解不唯一，可以知道一定可以构造出一个等腰三角形使得满足条件，可以看下图，对于一个确定的外接圆，已知底边和外接圆半径的话，是可以求出三边的，随着底边的缩小和伸长内切圆是先变大后变小，而最大的时候就是上述所说，等边的时候。所以知道了上下界，就可以直接二分底边了，二分的区间就是下图所标区间。

 #include <iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<stdlib.h>
 #include<vector>
 #include<cmath>
 #include<queue>
 #include<set>
 using namespace std;
 #define N 100000
 #define LL long long
 #define INF 0xfffffff
 const double eps = 1e-;
 const double pi = acos(-1.0);
 const double inf = ~0u>>;
 int dcmp(double x)
 {
     if(fabs(x)<eps) return ;
     return x<?-:;
 }
 int cal(double x,double R,double r)
 {
     if(dcmp(R*R-x*x)<) return ;
     double a = sqrt(*R*R+*R*sqrt(R*R-x*x));
     double b = a;
     double c = *x;
     double s = (a+b+c)/;
     double tt = (s-a)*(s-b)*(s-c)/s;
     if(dcmp(tt)<) return ;
     double tr = sqrt(tt);
     if(dcmp(tr-r)>=) return ;
     return ;
 }
 int main()
 {
     double r1,r2;
     while(scanf("%lf%lf",&r1,&r2)!=EOF)
     {
         if(dcmp(*r1-r2)>)
         {
             puts("NO Solution!");
             continue;
         }
         double rig = sqrt(3.0)*r2,lef = ,mid;
         while(rig-lef>eps)
         {
             mid = (lef+rig)/;
             if(cal(mid,r2,r1))
                 rig = mid;
             else lef = mid;
         }
        // printf("%f\n",rig);
         double a = sqrt(*r2*r2+*r2*sqrt(r2*r2-rig*rig));
         double b = a;
         double c = *rig;
         printf("%.15f %.15f %.15f\n",a,b,c);
     }
     return ;
 }