关于Graph Convolutional Network的初步理解

　　为给之后关于图卷积网络的科研做知识积累，这里写一篇关于GCN基本理解的博客。GCN的本质是一个图网络中，特征信息的交互+与传播。这里的图指的不是图片，而是数据结构中的图，图卷积网络的应用非常广泛 ，经常被举到的典型例子就是一个空间中热量的传递和交互，这里不多作赘述。

一、图卷积网络与普通卷积网络的应用范围

　　图卷积网络为什么叫图卷积网络呢？图卷积网络，其实就是就是GCN，但GCN为什么是图神经网络呢？小编也很疑惑。

　　好了！开玩笑的话先打住，进入正题。首先复习一下卷积神经网络的工作原理，以检测图片的过程为例，卷积神经网络提取图片特征的过程，其实就是对每个像素周边像素加权求和的过程，初始每个像素对应的卷积核的权重随机，在通过反向传递、逐层梯度下降的优化之后才会得到合理的权重，根据这个权重得到的feature map便是特征提取的结果。对于图像等像素排列规整的结构来说，使用普通的卷积神经网络提取特征没有任何问题，但对于某些形如交通网、电网等“不整齐”的结构，普通的CNN就没有用武之地了，引用知乎大佬学术性的话讲，就是“CNN在Non Euclidean Structure的数据上无法保持平移不变性”，翻译成人话就是对于图结构的数据，其每个点邻接的数量各不相同，会给CNN提取特征带来很大的困难；要提取图结构的空间特征进行后续的机器学习，就需要使用图卷积网络。简而言之，GCN是CNN的升级版，CNN做不到的，GCN可以做，GCN做的到的，CNN做不到。

二、图卷积网络提取空间特征的方式

　　提取拓扑图空间特征有两种方法：空间领域与谱领域。这里我只对谱领域的提取方法作总结概述（空间领域的没学），通过定义图上的傅里叶变换，图的卷积方式得到表示方式，与深度学习结合得到最终的图卷积网络。在进行傅里叶和卷积的推导前先复习一下线代？一张图的拉普拉斯矩阵一般为其度矩阵D减去其邻接矩阵A，其他常见定义也有D^-1LD与D^-1L。

1.图的特征分解

　　对图的拉普拉斯矩阵进行谱分解，说的通俗易懂一点就是对角化。使用拉普拉斯矩阵进行运算的优势在这里体现：拉普拉斯矩阵满足谱分解所需线性无关的条件。图的拉普拉斯矩阵分解形式为UPU-1，其中U=[u1，u2，…，un]，为列向量是单位特征向量的矩阵；P为含有n个特征值的对角矩阵。

2.含特征向量与特征值矩阵的傅里叶变换定义

　　在浏览一些大佬的博客与知乎时我常常感到诧异：进行完矩阵分解后怎么突然讲到傅里叶变化了？理清思路后发现相关矩阵傅里叶变换的定义是最后卷积公式推导的基础，由于两函数的卷积是其函数傅立叶变换乘积的逆变换，即：

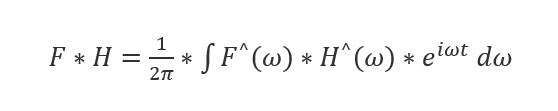
　　为了能将针对图的傅里叶变换类比代入上述公式，我们需要推广傅里叶变换，把特征函数 e^iωt 变为拉普拉斯矩阵的特征向量。

　　由傅里叶变换的一般形式：

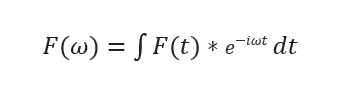
　　类比特征方程定义：

LV=λV

　　L、V、λ分别代表拉普拉斯矩阵、特征向量/函数、特征值。将特征向量与前面定义的u矩阵对应，得到最终图的傅里叶变换定义为：

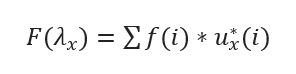
　　其中f(i)对应图的各个顶点，u_x^*(i)表示第x个特征向量的第 i 个分量。那么特征值λ_x下F的图傅里叶变换就是与λ_x对应的特征向量u_x进行内积运算。矩阵形式为：

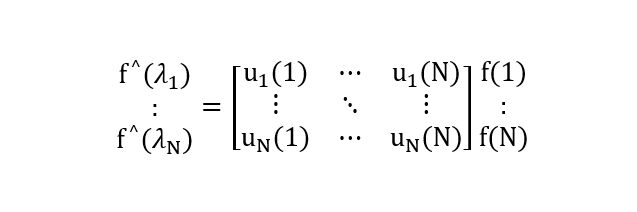
　　即f^=U^T f。同时由傅里叶逆变换基本公式：

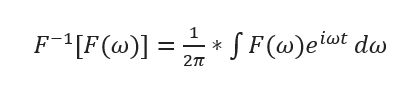
　　得到傅里叶逆变换的矩阵形式：

　　

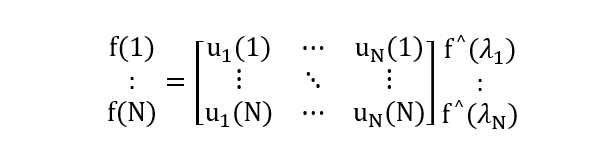
　　即f=Uf^。

3.图卷积推导　　

　　在定义完图上的傅里叶变换之后，总算要开始让梦想照进现实将卷积运算推广到图上了。由卷积定理：

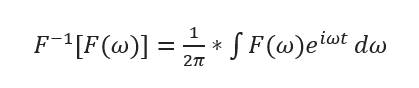
　    将对应图上各点的f与卷积核h的傅里叶定义代入其中，卷积核在图上的傅里叶变换被定义为：

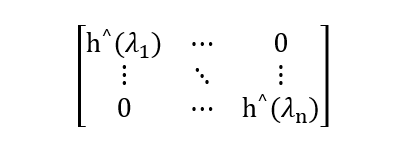
　　按卷积定理将两者傅里叶变换形式相乘得到：

　　最后乘U求得傅立叶变换乘积的逆变换，最终得到卷积：

　　以上，GCN粗略的推导过程就整理完毕了。

　　参考网站：　https://www.zhihu.com/question/54504471?sort=created

　　　　　　　　https://www.cnblogs.com/h2zZhou/p/8405717.html