POJ 1487：Single-Player Games 浮点数高斯消元

Single-Player Games

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 1287		Accepted: 362

Description

Playing games is the most fun if other people take part. But other players are not always available if you need them, which led to the invention of single-player games. One of the most well-known examples is the infamous ``Solitaire'' packaged with Windows,
probably responsible for more wasted hours in offices around the world than any other game. 

The goal of a single-player game is usually to make ``moves'' until one reaches a final state of the game, which results in a win or loss, or a score assigned to that final state. Most players try to optimize the result of the game by employing good strategies.
In this problem we are interested in what happens if one plays randomly. After all, these games are mostly used to waste time, and playing randomly achieves this goal as well as any other strategy. 



Games can very compactly represented as (possibly infinite) trees. Every node of the tree repre- sents a possible game state. The root of the tree corresponds to the starting position of the game. For an inner node, its children are the game states to which
one can move in a single move. The leaf nodes are the final states, and every one of them is assigned a number, which is the score one receives when ending up at that leaf. 




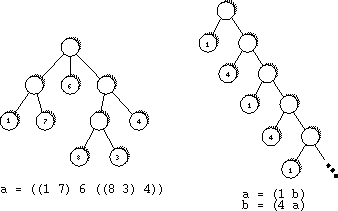
Trees are defined using the following grammar. 



Definition ::= Identifier "=" RealTree 

RealTree ::= "("Tree⁺")" 

Tree ::= Identifier | Integer | "("Tree⁺")" 

Identifier ::= a|b|...|z 

Integer ∈ {...,-3,-2,-1,0,1,2,3,...,}

By using a Definition, the RealTree on the right-hand side of the equation is assigned to the Identifier on the left. A RealTree consists of a root node and one or more children, given as a sequence enclosed in brackets. And a Tree is either 



. the tree represented by a given Identifier, or 



. a leaf node, represented by a single Integer, or 



. an inner node, represented by a sequence of one or more Trees (its children), enclosed in brackets. 



Your goal is to compute the expected score, if one plays randomly, i.e. at each inner node selects one of the children uniformly at random. This expected score is well-defined even for the infinite trees definable in our framework as long as the probability
that the game ends (playing randomly) is 1. 

Input

The input file contains several gametree descriptions. Each description starts with a line containing the number n of identifiers used in the description. The identifiers used will be the first n lowercase letters of the alphabet. The following n lines contain
the definitions of these identifiers (in the order a, b, ...). Each definition may contain arbitrary whitespace (but of course there will be no spaces within a single integer). The right hand side of a definition will contain only identifiers from the first
n lowercase letters. The inputs ends with a test case starting with n = 0. This test case should not be processed.

Output

For each gametree description in the input, first output the number of the game. Then, for all n identifiers in the order a, b, ..., output the following. If an identifier represents a gametree for which the probability of finishing the game is 1, print the
expected score (when playing randomly). This value should be exact to three digits to the right of the decimal point. 



If the game described by the variable does not end with probability 1, print ``Expected score of id undefined'' instead. Output a blank line after each test case.

Sample Input

1
a = ((1 7) 6 ((8 3) 4))
2
a = (1 b)
b = (4 a)
1
a = (a a a)
0

Sample Output

Game 1
Expected score for a = 4.917

Game 2
Expected score for a = 2.000
Expected score for b = 3.000

Game 3
Expected score for a undefined

题意是给出一个树，然后树上的根节点有相应的值，所有根节点 对应的值*树到达该根节点的概率 相加就是1。用深搜的方法列方程，每一个字符列一个方程，最后用高斯消元解方程。

这题出得很严谨，注意精度。

今天出了各种问题，这道题调了差不多4个小时。。。

#pragma warning(disable:4996)
#include <iostream>
#include <algorithm>
#include <cmath>
#include <vector>
#include <stdlib.h>
#include <string.h>
#include <string>
#include <cstring>
using namespace std;

#define eps 1e-6

int n, p, len;
char s[350];
int free_x[500];
double x[500];
double val[500][500];

inline double zero(double x)
{
	if (fabs(x) > eps)return x;
	return 0;
}
int Gauss(int equ, int var)
{
	int i, j, k;
	int max_r;//当前这列绝对值最大的行
	int col;//当前处理的列
	double tb;
	double temp;

	for (int i = 0; i <= var; i++)
	{
		x[i] = 0;
		free_x[i] = 1;
	}
	//转换为阶梯阵
	col = 0;//当前处理的列
	for (k = 0; k < equ&&col < var; k++, col++)
	{
		//枚举当前处理的行
		//找到该col列元素绝对值最大的那行与第k行交换.(为了在除法时减少误差)
		max_r = k;
		for (i = k + 1; i < equ; i++)
		{
			if (fabs(val[i][col])>fabs(val[max_r][col]))
				max_r = i;
		}
		if (max_r != k)
		{//与第k行交换
			for (j = k; j < var + 1; j++)
				swap(val[k][j], val[max_r][j]);
		}
		if (fabs(val[k][col]) < eps)
		{
			k--;
			continue;
		}
		for (i = k + 1; i < equ; i++)
		{//枚举要删去的行
			if (fabs(val[i][col]) > eps)
			{
				tb = val[i][col] / val[k][col];
				for (j = col; j < var + 1; j++)
				{
					val[i][j] = (val[i][j] - val[k][j] * tb);
				}
			}
		}
	}

	//无解的情况
	for (i = k; i < equ; i++)
	{
		if (val[i][col] > eps)
			return -1;
	}

	if (k < equ)
	{
		//注释处为求多解的自由变量
		// 首先，自由变元有n - k个，即不确定的变元至少有n - k个.
		int num = 0, freeidx;
		for (i = k - 1; i >= 0; --i)
		{
			num = 0;// 用于判断该行中的不确定的变元的个数，如果超过1个，则无法求解，它们仍然为不确定的变元.
			double tmp = val[i][n];
			// 第i行一定不会是(0, 0, ..., 0)的情况，因为这样的行是在第k行到第m行.
			// 同样，第i行一定不会是(0, 0, ..., a), a != 0的情况，这样的无解的.
			for (j = 0; j < n; ++j)
			{
				if (fabs(val[i][j])>eps && free_x[j])
				{
					num++;
					freeidx = j;
				}
			}
			if (num > 1) continue; // 无法求解出确定的变元.
								   // 说明就只有一个不确定的变元free_index，那么可以求解出该变元，且该变元是确定的.
			tmp = val[i][n];
			for (j = 0; j < n; ++j)
			{
				if (fabs(val[i][j])>eps && j != freeidx) tmp -= val[i][j] * x[j];
			}
			x[freeidx] = tmp / val[i][freeidx];
			free_x[freeidx] = 0;
		}
		return n - k;
	}

	for (i = var - 1; i >= 0; i--)
	{
		temp = val[i][var];
		for (j = i + 1; j < var; j++)
		{
			if (val[i][j])
			{
				temp = temp - val[i][j] * x[j];
			}
		}
		x[i] = temp / val[i][i];
	}
	return 0;
}

void dfs(double *a)
{
	int cnt = 0;
	while (s[p] != ')')
	{
		if (s[p] == ' ')
		{
			p++;
		}
		else if (s[p] == '(')
		{
			double b[50];
			p++;

			memset(b, 0, sizeof(b));
			dfs(b);
			cnt++;
			for (int k = 0; k <= n; k++)
			{
				a[k] += b[k];
			}
		}
		else if (s[p] >= '0'&&s[p] <= '9')
		{
			cnt++;
			int num = 0;
			while (s[p] >= '0'&&s[p] <= '9')
			{
				num = num * 10;
				num = num + s[p] - '0';
				p++;
			}
			a[n] += num;
		}
		else if (s[p] == '-')
		{
			cnt++;
			int num = 0;
			p++;
			while (s[p] >= '0'&&s[p] <= '9')
			{
				num = num * 10;
				num = num + s[p] - '0';
				p++;
			}
			a[n] -= num;
		}
		else if (s[p] >= 'a'&&s[p] <= 'z')
		{
			cnt++;
			a[s[p] - 'a']++;
			p++;
		}
	}

	if (cnt)
	{
		for (int k = 0; k <= 27; k++)
		{
			a[k] = a[k] / cnt;
		}
	}
	p++;
	return;
}

int main()
{
	//freopen("i.txt", "r", stdin);
	//freopen("o.txt", "w", stdout);

	int i, k, ans;
	int itest = 0;
	while (scanf("%d", &n) != EOF)
	{
		if (n == 0)
			break;

		getchar();
		memset(val, 0, sizeof(val));

		printf("Game %d\n", ++itest);
		for (i = 0; i < n; i++)
		{
			gets_s(s);//VS2015用gets_s代替了get

			p = 0;
			while (s[p] != '(')
				p++;
			p++;
			dfs(val[i]);
			for (k = 0; k < n; k++)
				val[i][k] = -val[i][k];
			val[i][i]++;
		}
		ans = Gauss(n, n);
		for (k = 0; k < n; k++)
		{
			if (ans == -1)
			{
				printf("Expected score for %c undefined\n", k + 'a');
			}
			else if (ans == 0)
			{
				printf("Expected score for %c = %.3lf\n", k + 'a',x[k]);
			}
			else
			{
				if (free_x[k])
					printf("Expected score for %c undefined\n", k + 'a');
				else
					printf("Expected score for %c = %.3lf\n", k + 'a', x[k]);
			}

		}
		printf("\n");
	}
	//system("pause");
	return 0;
}