【遗传编程/基因规划】Genetic Programming

目录

• 背景介绍
• 程序表示
• 初始化 (Initialization)
  • Depth定义
  • Grow方法
  • Full方法
  • Ramped half-and-half方法
• 适应度(Fitness)与选择(Selection)
  • Fitness & Fitness Function
  • 选择 Selection
• 遗传算子Genetic Operators
  • 交叉 Crossover
  • 变异 Mutation
  • 复制 Reproduction (Copy)
• 参考资料 (reference)

本篇博文提供了关于GP过程的总结型概览与讨论，旨在帮助初学者建立一个对GP的基础印象。主要参考文献 A Field Guide to Genetic Programming，后文中简写为"Field Guide1"。

文章转载自博文

背景介绍

“物竞天择，优胜劣汰”， 达尔文提出了著名的生物进化理论，即所有的动植物都是由较早期、较原始的形式演变而来的。而遗传编程（遗传规划）则在数学和计算机科学领域应用了这一演化过程：从基数较为庞大的原始、粗糙的程序种群中通过评估适应性选择父系、进行遗传操作生成新一代种群，再判断终止条件决定是否再次迭代、生成下一代种群。类比如下：





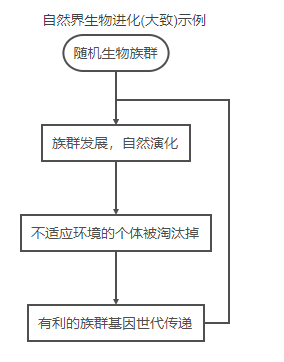
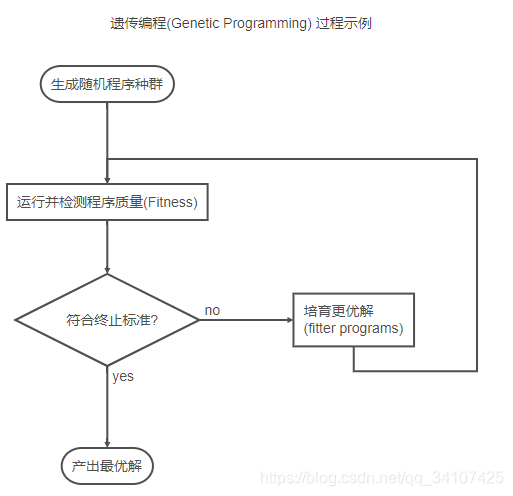
对照上面的流程图，我们可以来简单理清GP系统做了什么、想要做什么。

1. 初始化：在给定初始条件（包括terminal sets, function sets和参数）后生成随机种群
2. 通过(多种方法)比较，评估适应性(fitness evaluation)
3. 依据fitness进行概率性选择——“probabilistically selected based on fitness”
4. 被选择的程序作为父系，通过交叉(Crossover) ，变异(Mutation)， 复制(Reproduction)等遗传算子(genetic operators)生成下一代(next generation)
5. 判断是否符合终止标准(Termination Criterion)，没符合的话继续迭代

程序表示

遗传编程，Genetic Programming (GP)， 属于进化算法(Evolutionary Algorithms)的一种。GP继承了遗传算法(Genetic Algorithms)的基本思想， 即从父辈中择优繁育子辈；不同于遗传算法(GA)的传统编码（固定长度基因）模式，GP的个体是计算机程序，具备多样的表现形式。最常见的是基于树状(Tree-based)的遗传编程，可用树形结构来清晰地表达。GP在发展过程中自然也拓展了多种种类与表现形式，如线性(Linear GP)，基于图的遗传编程(Cartesian GP)等。



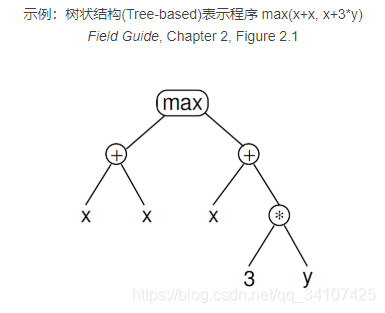
"Field Guide"一书提到在GP中，程序多用以syntax tree（如上）的方式来表现。关于syntax tree的结构定义如下：

• “树叶”部分被称为 终止符(Terminals) , 是程序中的变量、常量和无参函数等。
• 树形内部节点被称为函数(Functions), 有时也被称为primitives，涵盖程序中的函数与操作。
• GP系统的Primitive set为允许、可行的Functions和Terminals的集合。

在上面的max(x+x, x+3y)树状表示图中，终止符为x，y，3，函数为，+，，max。则他们分别的集合为：函数集(function set) F = {+, *, max}，终止集(terminal set) T = {x, y, 3}

注意：“函数”未必一定包含在函数集(function set)中，无参函数可能在终止集(terminal set)中

在一些GP中程序可能由多个部分组成，如下图，用一组由特殊根节点(root)连接结合的树形分支(sub-trees branches)来表示。

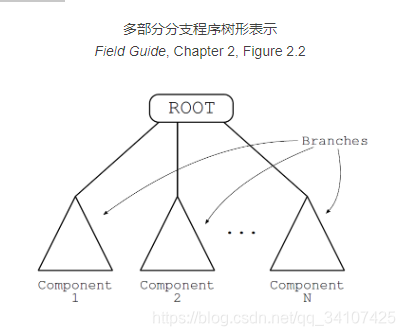
初始化 (Initialization)

在上文流程图部分，已提到GP的初始种群(initial population)一般是给定函数集，终止集和参数随机生成的。参数包括种群数量(population size)，决策树深度(depth)等。抛开参数、限制、种类不谈，我们可以将随机生成个体的事件视作从函数集和终止集随机取得元素，创建节点(根节点root或子节点)并为其指定连接的随机子节点的随机过程。

Depth定义

但如果抛开限制，树形结构种群会变得过于冗长笨拙、杂乱不堪，所以我们引入一个重要概念：深度。Field Guide 给出如下定义:



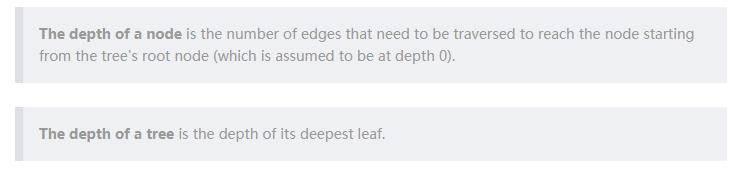
还是以上文中的 max(x+x, x+3*y) 树形表示为例：根节点 函数max的深度(depth)为0，观察右侧的子节点 函数 * ， 这个子节点的深度为2。从max到最底层“树叶” 3 和 y 走过了3条edges，故整个树的深度为3。

通过指定树的深度，我们可以控制树的大小以及复杂性、种群系统的复杂程度。注：并不是depth越大越好。depth越大，整体系统就越复杂、越难以理解，有可能产生过拟合。

回到初始化过程中来，随机生成个体的两种最早期、最简单的方法分别为grow method 和 full method。在两种方法中，初始个体深度都不能超过(用户)所指定的深度。

Grow方法

grow方法从函数集中随机选择函数作为根节点，从整个primitive set(函数集+终止集) 中随机选择作为子节点，直到达到限制的深度（或因可连接节点全部随机选择到terminals或无参函数而自动停止），达到限制的深度时只能从终止集(terminal set)中随机取用终止符作为leaves。

设函数集F={+, -, *, /}，终止集T={x, y, 0, 1, 2, 3}，给定深度depth=2，t=time，使用grow方法随机生成一个个体(例)，如下图：



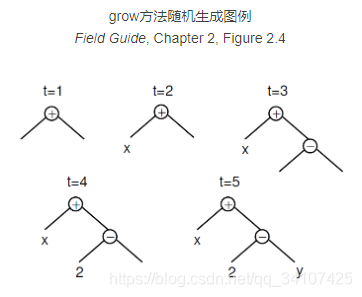
与full方法相比，grow生成的个体有着更为多样化的大小和形状

Full方法

full方法从函数集中随机取出函数作为根节点，从函数集中随机取出函数作为子节点，直到达到深度限制，达到指定深度时只能从终止集中随机取用终止符作为leaves。

仍设定函数集F={+, -, *, /}，终止集T={x, y, 0, 1, 2, 3}，给定深度depth=2，t=time，使用full方法随机生成一个个体(例)，如下图：

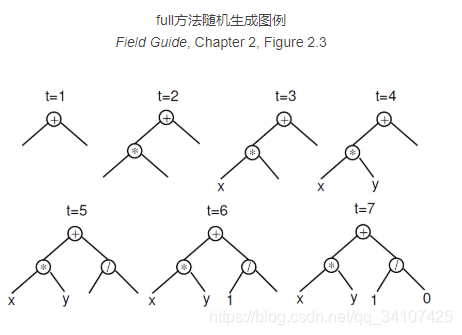
• full方法生成的初始个体中，所有的终止符都处于同一深度。
• 初始个体的节点数量不一定相同（函数集当中的函数参数数量可能不同，故连接到下一层的子节点数量可能有所不同）

Ramped half-and-half方法

由于grow和full方法都有着形状和大小上的局限性（初始个体深度需等于所指定的深度），1992年在Stanford任教的Koza教授提出了一种新的组合方法 Ramped half-and-half2。这种方法通过指定一个深度的范围（而不是单一深度限制），让一半种群总数量的个体实行grow方法生成、另一半则实行full方法生成。这样的方法移除了单一深度的限制，并且有着full和grow的混合使用，在树的形状和大小方面增强了多样性（而且依旧简单容易实现）。

注意事项：

以上的三种初始化方法相对都很原始，仍有较多的局限性，难以控制如形状和大小的统计分布。Field Guide 中给出了grow方法对函数集基数和终止集基数敏感、易受到影响而改变形状的例子：

适应度(Fitness)与选择(Selection)

Fitness & Fitness Function

适应度(fitness)：衡量个体优劣的一个数值，是评价个体解决问题质量的标准。类比自然界物种，对环境适应度高的生物种群将优良基因遗传下来，适应度差的被自然淘汰而灭绝。

适应度函数(fitness function)： 计算种群中个体的适应度的函数。

基于不同的问题，适应度可以用多样、不同的方式来衡量。如实际输出与期望输出之间的差值，系统演化到目标程度所花费的资源等等。

适应度评估过程所需时间占了一大部分GP系统运行所需时间，故fitness function的设计一般不建议过于复杂。本篇主讲概念，来对其产生一个初步印象。针对一个实际问题的适应度函数的构成和评估过程在之后几篇中会进行。

选择 Selection

选择，指的是基于适应度(fitness)选择个体的过程，被选择的个体在之后会作为父系通过遗传算子繁育下一代程序个体。常用选择方法有两种：

锦标赛选择法 (Tournament Selection)：

tournament selection从群体中随机取一定数量的个体，比较它们的适应度，适应度最高的被选为parent (作为父系)进行下一个步骤的遗传操作 (genetic operations)。由于每次进行选择时都是随机取一定数量的个体 (而不是整体) 进行比较，即使是平均质量、fitness在整个群体中来看并不突出的个体也有机会被选中，故此实现了多样性。

轮盘赌选择法 (Roulette Wheel Selection)：

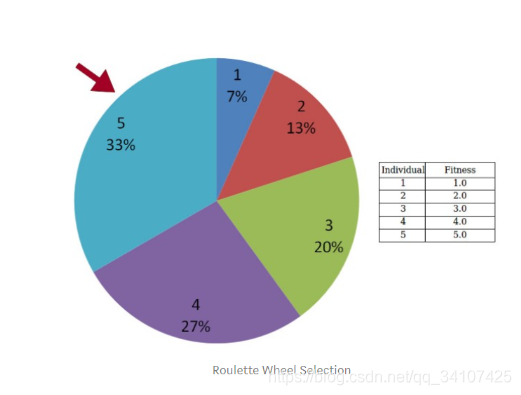
个体被选中的概率与其适应度成正比。设群体中存在个体1，个体2 … 到个体N(群体基数为N)，\(f_i\)表示个体i的适应度，则轮盘赌法选中个体i作为parent的概率为：



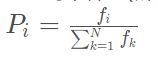
图示：设群体中共有五个个体，序号1~5的个体适应度分别为1.0，2.0，3.0，4.0，5.0，则随机选中个体5的概率为 5.0/(1.0+2.0+3.0+4.0+5.0) = 33.33%

遗传算子Genetic Operators

经过一轮选择得到适应性较好的父体后，遗传算子对父体(parent)进行遗传操作，生成子代(child)。遗传算子包括以下三种：

交叉 Crossover

两个父体基因的混合/交换。

常用的一种subtree crossover过程：在每一个父体中随机选择一个杂交点(crossover point)，复制其中一个父体的树为Acopy，复制第二个父体中以杂交点为根节点的子树(subtree) 为Bsubtree_copy，将Acopy杂交点下的子树替换为Bsubtree_copy，生成子体。图示如下：

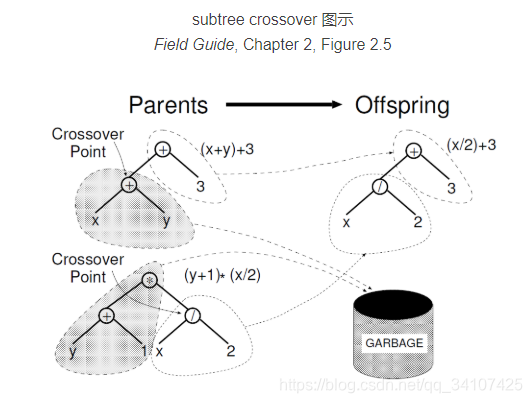
subtree crossover由两个父体随机生成了一个子体。其他多种交叉/杂交方法中，也存在由两个父体生成两个子体的种类，如one-point crossover。

变异 Mutation

一个父体的随即部分改变（变异）。

常用的一种subtree mutation：在一个父体中随机选择一个突变点(mutation point)，随机生成一个子树，将父体中以突变点为根节点的子树替换为这个随机生成的子树。

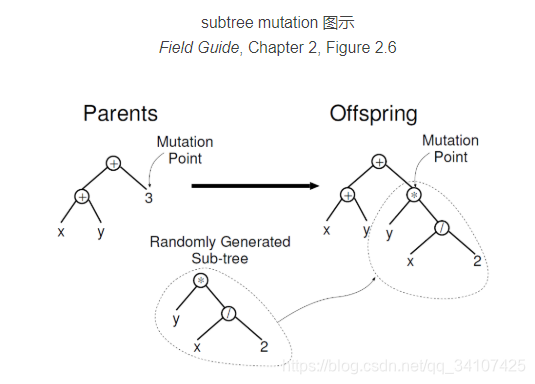
复制 Reproduction (Copy)

个体被直接复制到下一代个体中。

复制的 实行率 = (100% - crossover rate - mutation rate)

备注：选择哪种遗传算子对父体进行操作是完全随机的。一般来说，交叉的实行几率约90%或更高，变异的实行几率约1%左右。

参考资料 (reference)

• Poli, Riccardo, et al. A Field Guide to Genetic Programming. Lulu Press, 2008.
• Genetic Programming, Wikipedia, https://en.wikipedia.org/wiki/Genetic_programming
• 人工智能（4）遗传规划，简书， https://www.jianshu.com/p/cf33f7158295
• Amorim, Elisa P. Dos Santos, et al. “Comparison between Genetic Algorithms and Differential Evolution for Solving the History Matching Problem.” Computational Science and Its Applications – ICCSA 2012 Lecture Notes in Computer Science, 2012, pp. 635–648., doi:10.1007/978-3-642-31125-3_48.
• https://deap.readthedocs.io/en/master/tutorials/advanced/gp.html