APIO强掠计划（spfa+tarjan缩点）

强掠计划

题目大意：

\(Siruseri\) 城中的道路都是单向的。不同的道路由路口连接。按照法律的规定，在每个路口都设立了一个 \(Siruseri\) 银行的 \(ATM\) 取款机。令人奇怪的是， \(Siruseri\) 的酒吧也都设在路口，虽然并不是每个路口都设有酒吧。

\(Banditji\) 计划实施 \(Siruseri\) 有史以来最惊天动地的 抢劫。他将从市中心出发，沿着单向道路行驶，抢劫所有他途径的 \(ATM\) 机，最终他将在一个酒吧庆祝他的胜利。

使用高超的黑客技术，他获知了每个 \(ATM\) 机中可以掠取的现金数额。他希望你帮助他计算从市中心出发最后到达某个酒吧时最多能抢劫的现金总数。他可以经过同一路口或道路任意多次。但只要他抢劫过某个 \(ATM\) 机后，该 \(ATM\) 机里面就不会再有钱了。 例如，假设该城中有 \(6\) 个路口，道路的连接情况如下图所示：

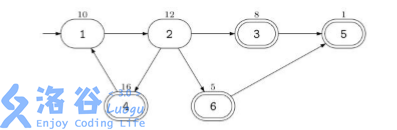
市中心在路口 \(1\) ，由一个入口符号 \(→\) 来标识，那些有酒吧的路口用双圈来表示。每个 \(ATM\) 机中可取的钱数标在了路口的上方。在这个例子中， \(Banditji\) 能抢劫的现金总数为 \(47\)，实施的抢劫路线是：\(1-2-4-1-2-3-5\)。

输入格式

第一行包含两个整数 \(N,M\)。\(N\) 表示路口的个数，\(M\) 表示道路条数。

接下来 \(M\) 行，每行两个整数，这两个整数都在 \(1\) 到 \(N\) 之间，第 \(i+1\) 行的两个整数表示第 \(i\) 条道路的起点和终点的路口编号。

接下来 \(N\) 行，每行一个整数，按顺序表示每个路口处的 \(ATM\) 机中的钱数 \(ai\)​。

接下来一行包含两个整数 \(S,P\)，\(S\) 表示市中心的编号，也就是出发的路口。\(P\) 表示酒吧数目。

接下来的一行中有 \(P\) 个整数，表示 \(P\) 个有酒吧的路口的编号。

输出格式

输出一个整数，表示 Banditji 从市中心开始到某个酒吧结束所能抢劫的最多的现金总数。

输入输出样例

输入

6 7
1 2
2 3
3 5
2 4
4 1
2 6
6 5
10
12
8
16
1
5
1 4
4 3 5 6

输出

47

题目思路：

这道题的主要思路就是tarjan先预处理一下。就这个例子说，我们可以看到1,2,4形成了一个权环，于是便可以把他们三个缩成一个点，然后再把原有的边连起来，然后求一个从开始的点开始的单源spfa，最后枚举酒吧的钱数求最大值。思路很清晰，缩点+spfa，主要还是看模板打的熟不熟练了。

废话不多说，上代码

#include <algorithm>
#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
const int Maxx = 1e7 + 10, INF = 0x3f3f3f3f;

int n, m;
int len, Head[Maxx], To[Maxx], from[Maxx], path[Maxx], t[Maxx];//cun
int len_, H[Maxx];
int low[Maxx], dfn[Maxx], stk[Maxx], top, num, belong[Maxx], cnt;//tarjan
long long w[Maxx];
bool vis[Maxx];
long long dis[Maxx];

struct Edge {
    int to, next;
} edge[Maxx], E[Maxx];

void addedge1(int a, int b) {
    edge[++len].to = b;
    edge[len].next = Head[a];
    Head[a] = len;
}
void addedge2(int a, int b) {
    E[++len_].to = b;
    E[len_].next = H[a];
    H[a] = len_;
}

void tarjan(int u) {
    low[u] = dfn[u] = ++num;
    stk[++top] = u;
    for (int x = Head[u]; x; x = edge[x].next) {
        int v = edge[x].to;
        if (!dfn[v]) {
            tarjan(v);
            low[u] = min(low[u], low[v]);
        } else if (!belong[v])
            low[u] = min(low[u], dfn[v]);
    }
    if (low[u] == dfn[u]) {
        ++cnt;
        while (1) {
            int x = stk[top--];
            belong[x] = cnt;
            w[cnt] += path[x];
            if (x == u) break;
        }
    }
}

void spfa(int s, int n) {
    queue<int> que;
    for (int i = 1; i <= n; i++) dis[i] = -INF, vis[i] = 0;
    dis[s] = w[s];
    que.push(s);
    vis[s] = 1;
    while (!que.empty()) {
        int u = que.front();
        que.pop();
        vis[u] = 0;
        for (int i = H[u]; i; i = E[i].next) {
            int v = E[i].to;
            if (dis[v] < dis[u] + w[v]) {
                dis[v] = dis[u] + w[v];
                if (!vis[v]) {
                    que.push(v);
                    vis[v] = 1;
                }
            }
        }
    }
}

void solve(){
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= m; i++) {
        scanf("%d%d", &from[i], &To[i]);
        addedge1(from[i], To[i]);
    }
    for (int i = 1; i <= n; i++) {
        scanf("%d", &path[i]);
    }
    int s, P;
    for (int i = 1; i <= n; i++)
        if (!dfn[i]) tarjan(i);

    scanf("%d%d", &s, &P);
    s = belong[s];
    int ansnum = 0;
    for (int i = 1; i <= P; i++) {
        int a;
        scanf("%d", &a);
        if (!vis[belong[a]]) {
            t[++ansnum] = belong[a];
            vis[belong[a]] = 1;
        }
    }
    for (int i = 1; i <= m; i++) {
        int u = belong[from[i]], v = belong[To[i]];
        if (u != v) addedge2(u, v);
    }
    spfa(s, cnt);
    long long ans = -INF;
    for (int i = 1; i <= ansnum; i++) {
        ans = max(ans, dis[t[i]]);
    }
    printf("%lld", ans);
}

int main(){
	solve();
	return 0;
}

谢谢观看