AC自动机（模板）

AC自动机是用来干什么的：

　　AC自动机是用来解决多模匹配问题，例如有单词s1，s2，s3，s4，s5，s6，问：在文本串ss中有几个单词出现过，类似。

AC自动机实现这个功能需要三个部分：

1、将所有单词用字典树的方法建树

2、构建失配指针

3、在文本串中的查找函数

这里主要讲2和3

一、建树

int tree[][],vis[],fail[];

int t,n,cnt,id,root,num=;

string s,ss;

void insert()//建树

{

    root=;

    for(int i=;s[i];i++)

    {

        id=s[i]-'a';

        if(tree[root][id]==)

            tree[root][id]=++num;

        root=tree[root][id];

    }

    vis[root]++;//单词结尾标记

}

二、构建失配指针

失配指针的作用是：当文本串在当前节点失配后，我们应该到哪个节点去继续匹配

失配指针起作用之后，可以求到在文本串中长度为[0，当前节点位置]的字串的最长公共后缀

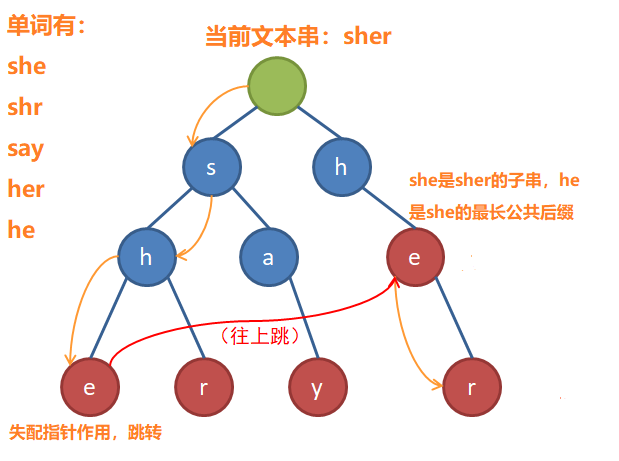
如何构建失配指针：

显然，我们要做的就是快速地求出所有点的fail指针。我们以bfs的顺序依次求出每个节点的fail，这样，当我们要求一个节点的fail时，它的父亲的fail肯定已经求出来了。若当前节点为A，其父节点为B，B的fail为C，那么C所代表的字符串一定是B的最长的后缀。如果C有一个儿子D的字符与A的字符等同，那么显然D所代表的串（C加一个字符）就是A所代表的串（B加一个字符）的最长后缀。如果C没有一个儿子，使其字符与A的字符等同呢？很简单，只需要再访问C的fail就行了。如此反复，直到A的最长后缀找到，或者A的fail指向根节点为止。（A在Trie树中没有后缀，乖乖回到根重新匹配吧！）

步骤：

为了少一些特判，设置一个辅助根节点0号节点，0号节点的所有儿子都指向真正的根节点1号节点，然后将1号节点的fail指向0号节点。
找到2号节点的父亲节点的fail节点0号节点，看0号节点有没有为a的子节点。有，于是2号节点的fail指向1号节点。
找到3号节点的父亲节点的fail节点0号节点，看0号节点有没有为b的子节点。有，于是3号节点的fail指向1号节点。
找到4号节点的父亲节点的fail节点1号节点，看1号节点有没有为b的子节点。有，于是4号节点的fail指向3号节点。
同上。
同上。
同上。
找到8号节点的父亲节点的fail节点5号节点，看5号节点有没有为b的子节点。没有，于是再找到5号节点的fail节点2号节点，看2号节点有没有为b的子节点。有，于是8号节点的fail指向4号节点。

代码：

void build()//构建失配指针

{

    queue<int>p;

    for(int i=;i<;i++)

    {

        if(tree[][i])//将第二行所有出现过的字母的失配指针指向root节点0

        {

            fail[tree[][i]]=;

            p.push(tree[][i]);

        }

    }

    while(!p.empty())

    {

        root=p.front();

        p.pop();

        for(int i=;i<;i++)

        {

            if(tree[root][i]==)//没有建树，不存在这个字母

                continue;

            p.push(tree[root][i]);

            int fa=fail[root];//fa是父亲节点

            while(fa&&tree[fa][i]==)//fa不为0，并且fa的子节点没有这个字母

                fa=fail[fa];//继续判断fa的父亲节点的子节点有没有这个字母

            fail[tree[root][i]]=tree[fa][i];//找到就构建失配指针

        }

    }

}

三、查找函数

for循环遍历一遍文本串，统计被标记的次数，记录最终答案

这里要注意的是，失配指针不仅仅是在失配的时候起作用

为了不让这种事情发生，我们每遇到一个fail指针就必须进行“失配”转移，以保证不会漏过任何一个子串，就像这样：

代码：

int search(string ss)//查找

{

    root=,cnt=;

    for(int i=;ss[i];i++)

    {

        id=ss[i]-'a';

        while(root&&tree[root][id]==)//失配转移

            root=fail[root];

        root=tree[root][id];

        int temp=root;

        while(vis[temp])

        {

            cnt=cnt+vis[temp];

            vis[temp]=;//清除标记，避免重复

            temp=fail[temp];

        }

    }

    return cnt;

}

优化

朴素的AC自动机的时间复杂度是不行的，原因如下：

匹配时因为每次都要跳fail边，复杂度上界可以达到 O(ml)

而Tire图就是用来解决这种问题的。可以想到，匹配时跳fail边是十分浪费时间的。举个例子，对于字符集{a,b,c}上的模式ab,aab,aaab,aaaab,ac和文本串aaaac，它们建出来的AC自动机和匹配过程是这样的（蓝色边是Trie树的边，红色边是fail指针，黄色边是匹配时的状态转移）：

我们会想，如果失配时可以一步到位就好了。每次跳fail边的过程是固定的：一直跳，直到找到拥有儿子c的节点为止。也就是说，无论什么时候在这个节点上失配，只要你找的是字符c，你总会在固定的节点上重新开始匹配。既然这样，不如直接把那个字符为c的节点变成自己的儿子，就可以省去跳fail边的麻烦：

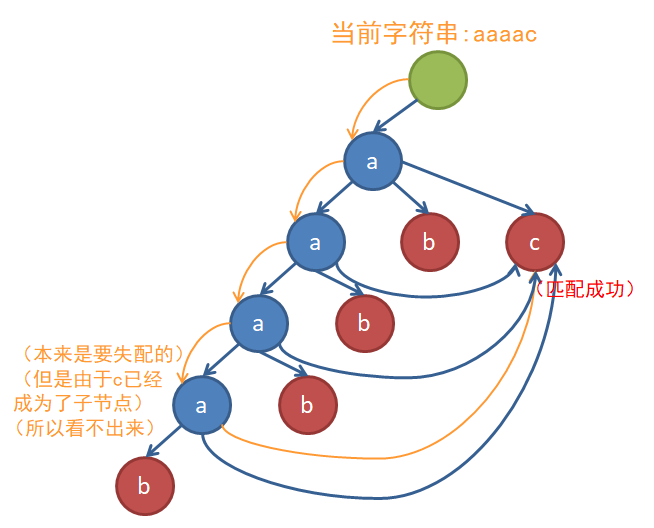
上图中，所有的节点的a,b,c三个子节点都是满的（未画出的边都指向根节点，表示完全失配只能从根重新开始）。这样，原本是DAG结构的AC自动机上出现了环，这样的结构我们称之为Trie图。于是乎，在匹配的时候我们终于可以不用考虑fail边，一口气不停地匹配到底辣٩(๑>◡<๑)۶复杂度变成了真正的 O(m)O(m)

void build()

{

    queue<int>p;

    fail[]=;

    for(int i=;i<;i++)

    {

        if(tree[][i]!=)

        {

            fail[tree[][i]]=;

            last[tree[][i]]=;

            p.push(tree[][i]);

        }

    }

    while(!p.empty())

    {

        root=p.front();

        p.pop();

        for(int i=;i<;i++)

        {

            if(tree[root][i]==)

            {

                tree[root][i]=tree[fail[root]][i];

                continue;

            }

            p.push(tree[root][i]);

            int temp=tree[root][i];

            int fa=fail[root];

            fail[temp]=tree[fa][i];

            last[temp]=(vis[fail[temp]]?fail[temp]:last[fail[temp]]);

        }

    }

}

last优化

上述方法将建图+匹配的复杂度成功优化为了 O(∑n+m)O(∑n+m) ，但是别忘了，匹配成功时的计数也是需要跳fail边的。然而，为了跳到一个结束节点，我们可能需要中途跳到很多没用的伪结束节点：

如果一个节点的fail指向一个结尾节点，那么这个点也成为一个（伪）结尾节点。在匹配时，如果遇到结尾节点，就进行相应的计数处理。

这里面就又有优化的余地了：对于不是真正结束节点的伪结束点，直接跳过它就好了。我们用一个last指针表示“在它顶上的fail边所指向的一串节点中，第一个真正的结束节点”。于是，每次计数处理时，我们不跳fail边，改为跳last边，省去了很多冗余操作。

获得last指针的方法也十分简单，就是在void build()中加一句话：

last[temp]=(vis[fail[temp]]?fail[temp]:last[fail[temp]]);

然后匹配时的代码就变成了：

void count(int x)

{

    if(x!=)

    {

        ans[vis[x]]++;

        count(last[x]);

    }

}

void search()

{

    root=;

    for(int i=;ss[i];i++)

    {

        id=ss[i];

        while(root&&tree[root][id]==)

            root=fail[root];

        root=tree[root][id];

        if(vis[root])

            count(root);

        else if(last[root])

            count(last[root]);

    }

}

以上转载自https://www.cnblogs.com/sclbgw7/p/9875671.html，谢谢博主

模板题：https://www.cnblogs.com/-citywall123/p/11300251.html

优化模板题：https://www.cnblogs.com/-citywall123/p/11319272.html