组合数的几种球阀 By cellur925

先来了解几个概念：排列数，组合数。

一、定义及有用的性质

排列数：从n个不同元素中依次取出m个元素排成一列的方案数。P(n,m)=n!/(n-m)!

组合数：从n个不同元素中依次取出m个元素形成一个集合的方案数。（注意，集合满足无序性，这是和排列数的区别）。C(n,m)=n!/m!(n-m)!

组合数性质

　　性质1 C(n,m)= C(n,n-m)

　　性质2 C(n,m)=C(n-1,m-1)+C(n-1,m)

　　性质3 C(n,0)+C(n,1)+C(n,2)+...+C(n,n)=2^n（道出组合数与杨辉三角间的联、系）

二、组合数球阀

① 递推 复杂度为n²

　 c[i][j]=c[i-1][j]+c[i-1][j-1]

但是要注意要命的初始化--

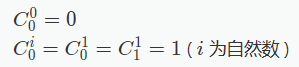
丢一段代码跑。

② 预处理阶乘+逆元 复杂度为nlogn

首先我们应该知道，除以一个数等于乘上这个数的逆元，那么我们就可以直接（生猛 地利用原始带有阶乘的公式，分母我们处理逆元。这里用到的是最简单的费马小定理方法，一个数x在膜p意义下的逆元等于x^(p-2）

丢一段代码跑。这个方法的使用条件是p为素数！

 #include<cstdio>
 #include<algorithm>

 using namespace std;
 typedef long long ll;
 const int p=1e9+;

 ll n,k,x;
 ll ans=;

 ll ksm(ll a,ll b)
 {
     ll tmp=;
     while(b)
     {
         if(b&) tmp=tmp*a%p;
         b>>=;
         a=a*a%p;
     }
     return tmp;
 }

 int main()
 {
     //求C(n,k)
     scanf("%d%d",&n,&k);
     for(int i=;i<=n;i++) ans=ans*i%p;
     for(int i=;i<=k;i++) ans=ans*ksm(i,p-)%p;
     for(int i=;i<=n-k;i++) ans=ans*ksm(i,p-)%p;
     printf("%lld",ans);
     return ;
 } 

*Update 费马小定理有的时候可能会复杂度爆炸 这里介绍一种exgcd求逆元的方法

 ll exgcd(ll a,ll b,ll &x,ll &y)
 {
     if(b==)
     {
           x=;
           y=;
           return a;
     }
     int gu=exgcd(b,a%b,x,y);
     int t=x;
     x=y;
     y=t-a/b*y;
     return gu;  

 }

 ll niyuan(ll hu)
 {
     x=,y=;
     ll tmp=exgcd(hu,p,x,y);
     return (x+p)%p;
 }

 ll C(ll k,ll m)
 {
     ll up=fac[k]%p;
     ll down=fac[m]%p*fac[k-m]%p;
     ll ans=up*niyuan(down)%p;
     return ans;
 }

③ 分解质因数 复杂度为nlogn

前导芝士：算术分解定理。

我们把分子分母都进行分解质因数，把整个分子分母对应的质因数的指数相减（消去）

丢一段代码跑。

 #include<cstdio>
 #include<algorithm>
 using namespace std;
 typedef long long LL;
 int n,m;
 int p;
 int i,j;
 int tot;
 int prim[],cnt[];
 bool flag[];

 void fj(int a,int k)//分解质因数 k=1/-1
 {//k==1时为分子操作 质因子数++
  //k==-1时为分母操作 质因子数--
     int x=a;
     for (int i=;i<=tot;i++)
     {
         if (x%prim[i]==)
         {
             while (x%prim[i]==) x/=prim[i],cnt[prim[i]]+=k;
         }
         if (x==) break;
         if (prim[i]*prim[i]>n) break;
     }
     if (x>) cnt[x]+=k;
 }

 int Pow(int x,int a)
 {
     int ans=; int j=;
     while (j<=a)
     {
         if (j&a) ans=((LL)ans*(LL)x)%p;
         j<<=;
         x=((LL)x*(LL)x)%p;
     }
     return ans;
 }

 int main()
 {
     scanf("%d%d%d",&n,&m,&p);
     //筛素数
     for (i=; i<=n; i++)
     {
         if (!flag[i]) prim[++tot]=i;
         for (j=; j<=tot; j++)
         {
             if (prim[j]*i>n) break;
             flag[prim[j]*i]=;
             if (i%prim[j]==) break;
         }
     }
     //printf("/////");
     int a=m; int b=(n-m);
     int c=max(a,b);
     //一定有一部分会自己消去（上下完全相同）
     for (i=c+; i<=n; i++)
     {//分子操作
         fj(i,);
     }
     //分母操作
     for (i=;i<=min(a,b);i++) fj(i,-);
     int ans=;
     for (i=; i<=n; i++)
     {
         if (cnt[i]>) ans=((LL)ans*Pow(i,cnt[i]))%p;
     }
     printf("%d\n",ans);
     return ;
  }