字符串匹配算法之BM算法

　　BM算法，全称是Boyer-Moore算法，1977年，德克萨斯大学的Robert S. Boyer教授和J Strother Moore教授发明了一种新的字符串匹配算法。

BM算法定义了两个规则：

1、坏字符规则：当文本串中的某个字符跟模式串的某个字符不匹配时，我们称文本串中的这个失配字符为坏字符，此时模式串需要向右移动，移动的位数 = 坏字符在模式串中的位置 - 坏字符在模式串中最右出现的位置。此外，如果"坏字符"不包含在模式串之中，则最右出现位置为-1。
2、好后缀规则：当字符失配时，后移位数 = 好后缀在模式串中的位置 - 好后缀在模式串上一次出现的位置，且如果好后缀在模式串中没有再次出现，则为-1。

关于坏字符规则和好后缀规则的具体讲解，以及怎么移动，可以查看阮一峰老师的详细讲解：http://www.ruanyifeng.com/blog/2013/05/boyer-moore_string_search_algorithm.html

这里根据讲解画了两张图，方便自己理解坏字符规则：

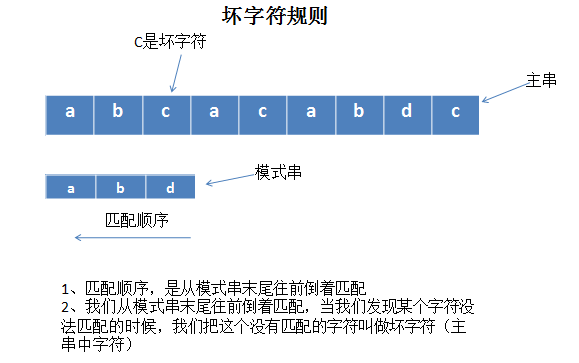
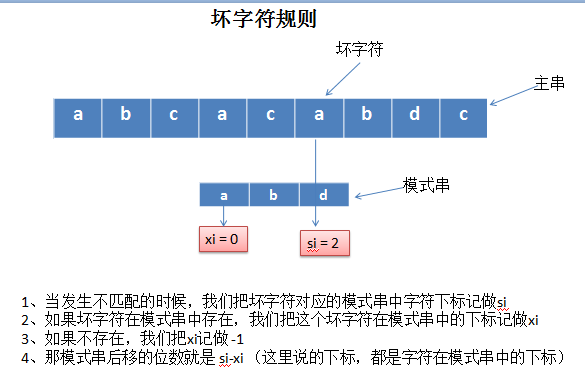
2019年11月14日15:38:41 修改

具体代码如下：

     private static final int SIZE = 256; // 全局变量或者是局部变量

     /**
      * 坏字符规则哈希表构建方法
      *
      * @param b
      *            模式串
      * @param m
      *            模式串的长度
      * @param bc
      *            散列表
      */
     private void generateBC(char[] b, int m, int[] bc) {
         for (int i = 0; i < SIZE; ++i) {
             bc[i] = -1; // 初始化bc
         }

         for (int i = 0; i < m; ++i) {
             int ascii = (int) b[i]; // 计算b[i]的ASCII值
             bc[ascii] = i;
         }
     }

     /**
      * 好后缀规则构建哈希表
      *
      * @param b
      *            模式串
      * @param m
      *            模式串长度
      * @param suffix
      *            suffix数组的下标 k，表示后缀子串的长度，
      *            下标对应的数组值存储的是，在模式串中跟好后缀{u}相匹配的子串{u*}的起始下标值
      * @param prefix
      *            记录模式串的后缀子串是否能匹配模式串的前缀子串
      */
     private void generateGS(char[] b, int m, int[] suffix, boolean[] prefix) {
         for (int i = 0; i < m; ++i) { // 初始化
             suffix[i] = -1;
             prefix[i] = false;
         }

         for (int i = 0; i < m - 1; ++i) {
             int j = i;
             int k = 0; // 公共后缀子串长度
             while (j >= 0 && b[j] == b[m - 1 - k]) { // 与b[0, m-1]求公共后缀子串
                 --j;
                 ++k;
                 suffix[k] = j + 1; // j+1表示公共后缀在b[0，i]中的起始下标
             }
             if (j == -1) {
                 prefix[k] = true; // 如果公共后缀子串也是模式串的后缀子串
             }
         }
     }

     /**
      * 完整的BM算法 好后缀+坏字符
      *
      * @param a
      *            主串
      * @param n
      *            主串的长度
      * @param b
      *            模式串
      * @param m
      *            模式串的长度
      * @return
      */
     public int bm(char[] a, int n, char[] b, int m) {
         int[] bc = new int[SIZE];
         generateBC(b, m, bc); // 构建坏字符哈希表
         int[] suffix = new int[m];
         boolean[] prefix = new boolean[m];
         generateGS(b, m, suffix, prefix); // 构建好字符哈希表
         int i = 0; // j 表示主串与模式串匹配的第一个字符
         while (i < n - m) {
             int j = 0;
             for (j = m - 1; j >= 0; --j) {// 模式串从后向前匹配
                 if (a[i + j] != b[j]) {
                     break; // 坏字符串
                 }
             }
             if (j < 0) {
                 return i;// 匹配成功，返回主串和模式串第一个匹配字符的位置
             }
             int x = j - bc[(int) a[i + j]];
             int y = 0;
             if (j < m - 1) { // 如果有好后缀的话
                 y = moveByGS(j, m, suffix, prefix);
             }
             i = i + Math.max(x, y);
         }
         return -1;
     }

     private int moveByGS(int j, int m, int[] suffix, boolean[] prefix) {
         int k = m - 1 - j; // 好后缀的长度
         if (suffix[k] != -1) {
             return j - suffix[k] + 1;
         }
         for (int r = j + 2; r <= m - 1; ++r) {
             if (prefix[m - r] == true) {
                 return r;
             }
         }
         return m;
     }    

现在再看BM算法，原来之前自己是一点也没弄懂！只是当做文章简单读了一遍，阿西吧！

首先，那个坏字符的散列表的构建就没有弄懂：

1、为什么在散列表数组中要初始化每一个值为-1？

这里是在坏字符匹配的时候，如果主串与模式串中字符没有匹配上（把坏字符在模式串中下标记做xi），此时的xi=-1

2、你有没有考虑过模式串中的相同的字符的ASCII码是相同的，那样循环处理的话，只是记录模式串中相同字符中最后面的那个字符的下标，没有问题吗？

这个是没有问题的！这里无非有两种情况，就是坏字符与非坏字符：

坏字符：因为是从后向前倒序匹配，只需要知道后面的字符下标，就可以计算出移动距离

非坏字符：需要去寻找坏字符或者使用好后缀规则

2019年11月14日15:34:37 修改

此大部分内容来自极客时间专栏，王争老师的《数据结构与算法之美》

极客时间：https://time.geekbang.org/column/intro/126