【模板】插头dp

题目描述

题解：

插头$dp$中经典的回路问题。

首先了解一下插头。

一个格子，上下左右四条边对应四个插头。就像这样：

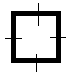
四个插头。

一个完整的哈密顿回路，经过的格子一定用且仅用了两个插头。

所以所有被回路经过的格子有六种状态，即左上，左右，左下，上右，上下，右下。

这几个就是插头$dp$的基本。

然后我们来了解一下轮廓线。

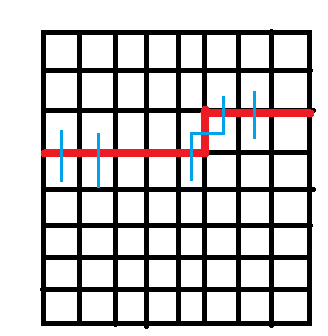
红线就叫轮廓线。

我们可以利用轮廓线作为状态dp，将轮廓线一点点右推+下推，直到推完，这样我们就可以得出全局答案啦！！！

但是怎么转移……

插头！

我们可以稍微讨论一下，讨论拐角处的插头状态，然后转移就好了。

听起来很简单恶心。

实际上很简单恶心。

现在我们突然想到一个问题，就是状态怎么记录。

主要有两种方法，一种叫最小表示法（不是字符串的最小表示法），一种叫括号序列。

最小表示法，是将互相联通的插头归入一类。如果我们将其采用字典序最小的方法表示，那么对于某条轮廓线表示法与轮廓线状态一一对应。

括号表示法，是由于网格中两条哈密顿回路路径不可相交的性质。

如果我们认为回路有方向，比如轮廓线左面的为进，右面的为出，那我们可以将进看作‘（’，将出看作‘）’。

由于上面那条性质，我们可以知道一个括号序列对应一种轮廓线状态。

而且括号表示法比最小表示法好写。

括号表示法怎么用？

三进制。0表示'-'，1表示'（'，2表示'）'。

压成一个数字然后用挂链存起来就好了。

（我用的括号表示法）

现在我们就差转移了。

（其实我非常不愿意在博客里写但是良心的我还是写了）

状态1：）（

直接用下面这个接上即可。

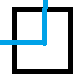
而且刚好满足括号匹配。

状态2：（-或）-

两种情况。

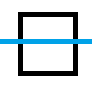或

状态3：-）或-（

还是两种情况。

或

状态4：））或（（

这个我们还是要放状态1的那个块。

但是不满足括号匹配怎么办？

向左/向右找一个换上。

举个例子，比如说原序列是：（（）（（）））（）（），

然后中间两个接在一起，序列就应该成为：（（）（）--）（）（）

注意那个变号。

状态5：--

直接放插头。

状态6：（）

一旦合并说明括号序列清空。

所以只能在最后一格合并状态6。

所以我们要知道最后一格在哪。

没有状态7。

上述状态都是在当前格子可填且插头指向格子可填时可选。

然后上代码：

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define N 15
#define ll long long
#define M 100000
int n,m;
ll bas[N];
char ch[N][N];
struct Map
{
    int hed[M+],cnt[];
    struct EG
    {
        int nxt;ll to,w;
    }e[<<][];
    void ae(int f,ll t,ll w,int k)
    {
        e[++cnt[k]][k].to = t;
        e[cnt[k]][k].nxt = hed[f];
        e[cnt[k]][k].w = w;
        hed[f] = cnt[k];
    }
    void push(ll u,ll d,int k)
    {
        int f = (int)(u%M);
        for(int j=hed[f];j;j=e[j][k].nxt)
            if(e[j][k].to==u)
            {
                e[j][k].w+=d;
                return ;
            }
        ae(u%M,u,d,k);
    }
    void clear(int k)
    {
        memset(hed,,sizeof(hed));
        cnt[k] = ;
    }
}mp;
ll ans;int tx,ty;
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=;i<=n;i++)
    {
        scanf("%s",ch[i]+);
        for(int j=;j<=m;j++)
            if(ch[i][j]=='.')
                tx=i,ty=j;
    }
    bas[] = ;
    for(int i=;i<=m+;i++)bas[i]=bas[i-]<<;
    mp.push(,,);
    for(int k=,i=;i<=n;i++)
    {
        for(int j=;j<=mp.cnt[k];j++)mp.e[j][k].to<<=;
        for(int j=;j<=m;j++)
        {
            k^=;mp.clear(k);
            for(int o=;o<=mp.cnt[!k];o++)
            {
                ll now = mp.e[o][!k].to,val = mp.e[o][!k].w;
                int lp = (now>>(j-)*)&,rp = (now>>j*)&;
                if(ch[i][j]=='*')
                {
                    if(!lp&&!rp)
                    {
                        mp.push(now,val,k);
                    }
                }else
                {
                    if(!lp&&!rp)
                    {
                        if(ch[i+][j]=='.'&&ch[i][j+]=='.')
                        {
                            ll tmp = now+bas[j-]+bas[j]*;
                            mp.push(tmp,val,k);
                        }
                    }else if(!lp&&rp)
                    {
                        if(ch[i+][j]=='.')
                        {
                            ll tmp = now+bas[j-]*rp-bas[j]*rp;
                            mp.push(tmp,val,k);
                        }
                        if(ch[i][j+]=='.')
                        {
                            ll tmp = now;
                            mp.push(tmp,val,k);
                        }
                    }else if(lp&&!rp)
                    {
                        if(ch[i+][j]=='.')
                        {
                            ll tmp = now;
                            mp.push(tmp,val,k);
                        }
                        if(ch[i][j+]=='.')
                        {
                            ll tmp = now-bas[j-]*lp+bas[j]*lp;
                            mp.push(tmp,val,k);
                        }
                    }else
                    {
                        if(lp==&&rp==)
                        {
                            ll tmp = now-bas[j-]-bas[j];
                            int sum = ;
                            for(int j0=j+;j0<=m+;j0++)
                            {
                                if(((now>>(j0-)*)&)==)sum++;
                                if(((now>>(j0-)*)&)==)sum--;
                                if(!sum)
                                {
                                    mp.push(tmp-bas[j0-],val,k);
                                    break;
                                }
                            }
                        }else if(lp==&&rp==)
                        {
                            ll tmp = now-bas[j-]*-bas[j]*;
                            int sum = ;
                            for(int j0=j-;j0>=;j0--)
                            {
                                if(((now>>(j0-)*)&)==)sum--;
                                if(((now>>(j0-)*)&)==)sum++;
                                if(!sum)
                                {
                                    mp.push(tmp+bas[j0-],val,k);
                                    break;
                                }
                            }
                        }else
                        {
                            if(lp==&&rp==)
                            {
                                ll tmp = now-bas[j-]*-bas[j];
                                mp.push(tmp,val,k);
                            }else if(i==tx&&j==ty)ans+=val;
                        }
                    }
                }
            }
        }
    }
    printf("%lld\n",ans);
    return ;
}