Uvalive 4043 Ants —— 二分图最大权匹配 KM算法

题目链接：https://vjudge.net/problem/UVALive-4043

题意：

给出n个白点和n个黑点的坐标， 要求用n条不相交的线段把他们连接起来，其中每条线段恰好连接一个白点和黑点，每个点恰好连接到一条线段。输出每个白点与其相连的黑点的编号。

题解：

1.首先随便配对。然后，如果存在两对黑白点的线段是相交的，那么就交换他们的配对对象。交换之后重新形成的线段就不会相交了（画画图就可看出）。而且可以推出一个结论：交换之后，两条线段之和必定变小。这是因为根据三角形定理：

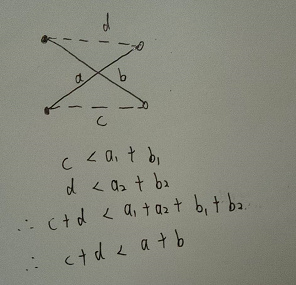
2.有了上述结论之后，我们就能推出：对于当前配对，如果线段总和还能继续变小，那么就可能存在交叉；但如果线段总和不能再小了，即已经达到最小，那么就不存在交叉了。所以我们只需要求最大权匹配（边权取反），就能满足要求了。

代码如下：

 #include <bits/stdc++.h>
 using namespace std;
 typedef long long LL;
 const int INF = 2e9;
 const LL LNF = 9e18;
 const double EPS = 1e-;
 const int MOD = 1e9+;
 const int MAXN = 1e2+;

 struct Node{
     double x, y;
 }black[MAXN], white[MAXN];

 int nx, ny;
 double  g[MAXN][MAXN];
 int linker[MAXN];
 double lx[MAXN], ly[MAXN], slack[MAXN];
 bool visx[MAXN], visy[MAXN];

 bool DFS(int x)
 {
     visx[x] = true;
     for(int y = ; y<=ny; y++)
     {
         if(visy[y]) continue;
         double tmp = lx[x] + ly[y] - g[x][y];
         if(tmp<EPS)
         {
             visy[y] = true;
             if(linker[y]==- || DFS(linker[y]))
             {
                 linker[y] = x;
                 return true;
             }
         }
         else
             slack[y] = min(slack[y], tmp);
     }
     return false;
 }

 void KM()
 {
     memset(linker, -, sizeof(linker));
     memset(ly, , sizeof(ly));
     for(int i = ; i<=nx; i++)
     {
         lx[i] = -INF;
         for(int j = ; j<=ny; j++)
             lx[i] = max(lx[i], g[i][j]);
     }

     for(int x = ; x<=nx; x++)
     {
         for(int i = ; i<=ny; i++)
             slack[i] = INF;
         while(true)
         {
             memset(visx, , sizeof(visx));
             memset(visy, , sizeof(visy));

             if(DFS(x)) break;
             double d = INF;
             for(int i = ; i<=ny; i++)
                 if(!visy[i])
                     d = min(d, slack[i]);

             for(int i = ; i<=nx; i++)
                 if(visx[i])
                     lx[i] -= d;
             for(int i = ; i<=ny; i++)
             {
                 if(visy[i]) ly[i] += d;
                 else slack[i] -= d;
             }
         }
     }
 }

 int main()
 {
     int kase = , n;
     while(scanf("%d", &n) != EOF)
     {
         if(kase++) printf("\n");

         nx = ny = n;
         for (int i = ; i <= n; i++)
             scanf("%lf%lf", &black[i].x, &black[i].y);
         for (int i = ; i <= n; i++)
             scanf("%lf%lf", &white[i].x, &white[i].y);

         for (int i = ; i <= n; i++)
         {
             double x1 = white[i].x, y1 = white[i].y;
             for (int j = ; j <= n; j++)
             {
                 double x2 = black[j].x, y2 = black[j].y;
                 g[i][j] = -sqrt( (x1-x2)*(x1 - x2) + (y1-y2)*(y1-y2) );
             }
         }

         KM();
         for(int i = ; i<=n; i++)
             printf("%d\n", linker[i]);
     }
 }