CS231n 2016 通关 第二章-KNN 作业分析

KNN作业要求：

1、掌握KNN算法原理

2、实现具体K值的KNN算法

3、实现对K值的交叉验证

1、KNN原理见上一小节

2、实现KNN

　　过程分两步：

　　　　1、计算测试集与训练集的距离

　　　　2、通过比较label出现比例的方式，确定选取的最终label

　　代码分析：

　　cell1 - cell5 对数据的预处理

　　cell6创建KNN类，初始化类的变量，此处是传递测试数据和训练数据

　　cell7实现包含两个循环的KNN算法：

　　　　通过计算单一的向量与矩阵之间的距离（在之前的cell中，已经将图像转换成列：32*32 的图像转换为 1*3072,，

　　　　测试集是500张：500*3072，训练集是5000张：5000*3072）

　　代码基础：使用python 2.7.9 + numpy 1.11.0

　　技巧：使用help 查看相关函数的用法，或者google

　　　　举例：np.square

　　　　　　　　　　

　　　　　　q 键退出help　　　　　　

　　　　　　

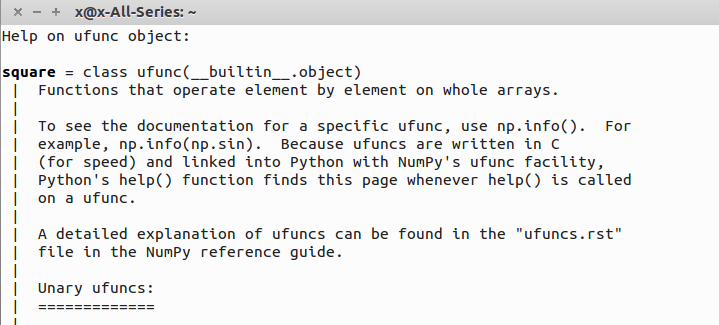
　　　　　　可知，np.square() 为了加快运算速度，是用c写的，在这里查不到具体用法。google查看:

　　　　　　

　　　　　　　　例子为计算数组[-1j,1]里边各元素的平方，得到的结果为[-1,1]

　　代码：实现compute_distances_two_loops(self, X)

 1   def compute_distances_two_loops(self, X):
     """
     Compute the distance between each test point in X and each training point
     in self.X_train using a nested loop over both the training data and the
     test data.

     Inputs:
     - X: A numpy array of shape (num_test, D) containing test data.

     Returns:
     - dists: A numpy array of shape (num_test, num_train) where dists[i, j]
       is the Euclidean distance between the ith test point and the jth training
       point.
     """
     num_test = X.shape[0]
     num_train = self.X_train.shape[0]
     dists = np.zeros((num_test, num_train))
     for i in xrange(num_test):
       for j in xrange(num_train):
         #####################################################################
         # TODO:                                                             #
         # Compute the l2 distance between the ith test point and the jth    #
         # training point, and store the result in dists[i, j]. You should   #
         # not use a loop over dimension.                                    #
         #####################################################################
         dists[i,j] = np.sqrt(np.sum(np.square(X[i,:]-self.X_train[j,:])))
         #####################################################################
         #                       END OF YOUR CODE                            #
         #####################################################################
     return dists

　　　　实现对一张测试图像对应的矩阵与一张训练集图像的矩阵做L2距离。

　　　　也可以用numpy.linalg.norm函数实现：

　　　　　　此函数执行的公式：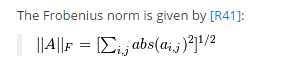

　　　　　　所以核心代码可以写作：

　　　　　　　　dists[i,j] = np.linalg.norm(self.X_train[j,:]-X[i,:])

　　cell8 得到的距离可视化，白色表示较大的距离值，黑色是较小距离值

　　cell9 实现K=1的label预测

　　代码：实现 classifier.predict_labels()

   def predict_labels(self, dists, k=1):
     """
     Given a matrix of distances between test points and training points,
     predict a label for each test point.

     Inputs:
     - dists: A numpy array of shape (num_test, num_train) where dists[i, j]
       gives the distance betwen the ith test point and the jth training point.

     Returns:
     - y: A numpy array of shape (num_test,) containing predicted labels for the
       test data, where y[i] is the predicted label for the test point X[i].
     """
     num_test = dists.shape[0]
     y_pred = np.zeros(num_test)
     for i in xrange(num_test):
       # A list of length k storing the labels of the k nearest neighbors to
       # the ith test point.
       closest_y = []
       count = []
       #########################################################################
       # TODO:                                                                 #
       # Use the distance matrix to find the k nearest neighbors of the ith    #
       # testing point, and use self.y_train to find the labels of these       #
       # neighbors. Store these labels in closest_y.                           #
       # Hint: Look up the function numpy.argsort.                             #
       #########################################################################
       buf_labels = self.y_train[np.argsort(dists[i,:])]
       closest_y = buf_labels[0:k]
       #########################################################################
       # TODO:                                                                 #
       # Now that you have found the labels of the k nearest neighbors, you    #
       # need to find the most common label in the list closest_y of labels.   #
       # Store this label in y_pred[i]. Break ties by choosing the smaller     #
       # label.                                                                #
       #########################################################################
       #for j in closest_y :
       #  count.append(closest_y.count(j))
       #m = max(count)
       #n = count.index(m)
       #y_pred[i] = closest_y[n]
       c = Counter(closest_y)
       y_pred[i] = c.most_common(1)[0][0]
       #########################################################################
       #                           END OF YOUR CODE                            #
       #########################################################################

     return y_pred

　　　　　　　　步骤：

　　　　　　　　　　1.使用numpy.argsort对所以距离进行排序，得到排序后的索引。

　　　　　　　　　　2.通过索引找到对应的label

　　　　　　　　　　3.通过collection包的Counter，对label进行统计表示

　　　　　　　　　　4.通过counter的Most common方法得到出现最多的label

　　cell9 在计算完成后，同时实现了准确率的计算

　　cell10 实现K =5的KNN

　　cell11 实现compute_distances_one_loop(X_test)

　　代码：

   def compute_distances_one_loop(self, X):
     """
     Compute the distance between each test point in X and each training point
     in self.X_train using a single loop over the test data.

     Input / Output: Same as compute_distances_two_loops
     """
     num_test = X.shape[0]
     num_train = self.X_train.shape[0]
     dists = np.zeros((num_test, num_train))
     for i in xrange(num_test):
       #######################################################################
       # TODO:                                                               #
       # Compute the l2 distance between the ith test point and all training #
       # points, and store the result in dists[i, :].                        #
       #######################################################################
       buf = np.square(self.X_train-X[i,:])
       dists[i,:] = np.sqrt(np.sum(buf,axis=1))
       #######################################################################
       #                         END OF YOUR CODE                            #
       #######################################################################
     return dists

　　并通过计算一个循环与两个循环分别得到的结果的差值平方，来衡量准确性。

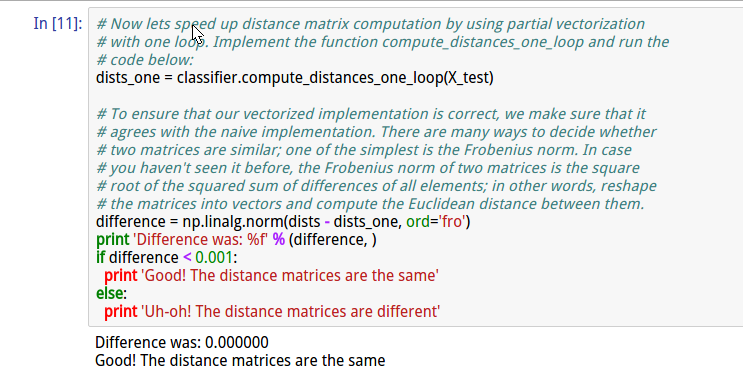
　　cell12 实现完全的数组操作，不使用循环。

   def compute_distances_no_loops(self, X):
     """
     Compute the distance between each test point in X and each training point
     in self.X_train using no explicit loops.

     Input / Output: Same as compute_distances_two_loops
     """
     num_test = X.shape[0]
     num_train = self.X_train.shape[0]
     dists = np.zeros((num_test, num_train))
     #########################################################################
     # TODO:                                                                 #
     # Compute the l2 distance between all test points and all training      #
     # points without using any explicit loops, and store the result in      #
     # dists.                                                                #
     #                                                                       #
     # You should implement this function using only basic array operations; #
     # in particular you should not use functions from scipy.                #
     #                                                                       #
     # HINT: Try to formulate the l2 distance using matrix multiplication    #
     #       and two broadcast sums.                                         #
     #########################################################################
     #buf = np.tile(X,(1,num_train))
     buf = np.dot(X, self.X_train.T)
     buf_test = np.square(X).sum(axis = 1)
     buf_train = np.square(self.X_train).sum(axis = 1)
     dists = np.sqrt(-2*buf+buf_train+np.matrix(buf_test).T)
     #########################################################################
     #                         END OF YOUR CODE                              #
     #########################################################################
     return dists

　　使用(a-b)²=a²+b²-2ab 的公式

　　27行： 此时buf_test 为500*1数组　　buf_train为5000*1的数组　　需要得到500*5000的数组　　此处通过构造矩阵的方式进行broadcast

　　cell13 比较3种方案的执行效率

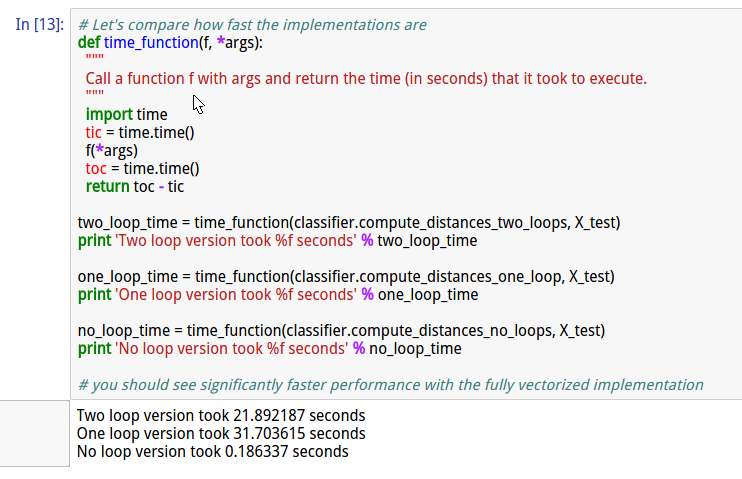
　　cell14 交叉验证

　　交叉验证的思想在上一节有解释过了

　　代码：（其中带有注释）

 num_folds = 5
 k_choices = [1, 3, 5, 8, 10, 12, 15, 20, 50, 100]

 X_train_folds = []
 y_train_folds = []
 ################################################################################
 # TODO:                                                                        #
 # Split up the training data into folds. After splitting, X_train_folds and    #
 # y_train_folds should each be lists of length num_folds, where                #
 # y_train_folds[i] is the label vector for the points in X_train_folds[i].     #
 # Hint: Look up the numpy array_split function.                                #
 ################################################################################
 X_train_folds = np.array_split(X_train, num_folds)
 y_train_folds = np.array_split(y_train, num_folds)
 ################################################################################
 #                                 END OF YOUR CODE                             #
 ################################################################################

 # A dictionary holding the accuracies for different values of k that we find
 # when running cross-validation. After running cross-validation,
 # k_to_accuracies[k] should be a list of length num_folds giving the different
 # accuracy values that we found when using that value of k.
 k_to_accuracies = {}

 ################################################################################
 # TODO:                                                                        #
 # Perform k-fold cross validation to find the best value of k. For each        #
 # possible value of k, run the k-nearest-neighbor algorithm num_folds times,   #
 # where in each case you use all but one of the folds as training data and the #
 # last fold as a validation set. Store the accuracies for all fold and all     #
 # values of k in the k_to_accuracies dictionary.                               #
 ################################################################################
 for k in k_choices:
     k_to_accuracies[k] = []

 for k in k_choices:
     print 'evaluating k=%d' % k
     for j in range(num_folds):
         #get validation
         X_train_cv = np.vstack(X_train_folds[0:j]+X_train_folds[j+1:])
         X_test_cv = X_train_folds[j]
         y_train_cv = np.hstack(y_train_folds[0:j]+y_train_folds[j+1:])
         y_test_cv = y_train_folds[j]
         #train
         classifier.train(X_train_cv, y_train_cv)
         dists_cv = classifier.compute_distances_no_loops(X_test_cv)
         #get accuracy
         y_test_pred = classifier.predict_labels(dists_cv, k)
         num_correct = np.sum(y_test_pred == y_test_cv)
         accuracy = float(num_correct) / num_test
         #add j th accuracy of k to array
         k_to_accuracies[k].append(accuracy)
 ################################################################################
 #                                 END OF YOUR CODE                             #
 ################################################################################

 # Print out the computed accuracies
 for k in sorted(k_to_accuracies):
     for accuracy in k_to_accuracies[k]:
         print 'k = %d, accuracy = %f' % (k, accuracy)

　　cell15 显示k值对应的准确率

　　上述包含了均值和标准差

　　cell16 使用最优值，得到较好的准确率

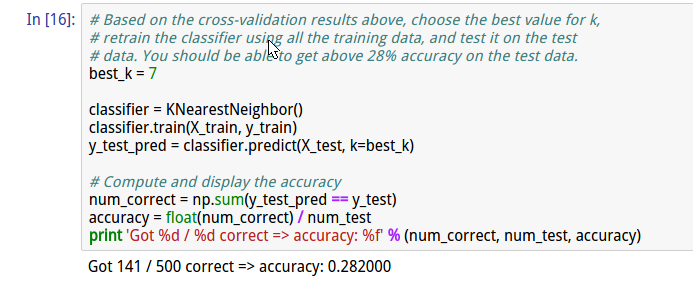
总结：

　　整体来说，第一个作业难度较大，主要难度不是在算法部分，而是在熟悉python相关函数与相应的用法方面。对于python大神而言，难度低。

　　但是经过扎实的第一次作业后，后边的作业相对简单了。之后的作业细节方面讲解的少些。

附：通关CS231n企鹅群：578975100 validation：DL-CS231n