【洛谷3546_BZOJ2803】[POI2012]PRE-Prefixuffix（String Hash）

Problem:

洛谷3546

Analysis：

I gave up and saw other's solution when I had nearly thought of the method ... What a pity

Let's define a border of string \(s\) as a prefix \(p\) of \(s\) that \(p\) is also a suffix of \(s\), and \(p\) is not longer than half of \(s\). What the problem asked us to look for is a number \(L\), that the prefix of length \(L\) can be divided into two string \(s1\) and \(s2\) , and the suffix of length \(L\) can be divided into two string \(s2\) and \(s1\), so that this pair of prefix and suffix is cyclically equivalent. Obviously, \(s1\) is a border of string \(s\). Another fact is, if \(s1\) is of length \(len\), \(s2\) is a border of the substring \([len, n - len - 1]\). Define \(f[len]\) as the length of the maximum border of the substring \([len, n - len - 1]\) . Let's enumerate the length of \(s1\) as \(len\) brutely, and for all legal \(len\) ("legal" means the prefix of length \(len\) is a border of \(s\). We can check it by hashing in \(O(1)\) time), the answer is \(len + f[len]\).

Now the problem is how to calculate \(f[len]\). Brute force takes \(O(n^2)\) complexity, but the useful fact below can decrease the complexity to \(O(n)\) :

\[f[i]\leq f[i+1]+2
\]

To make it easy, look at the (beautiful) picture below.

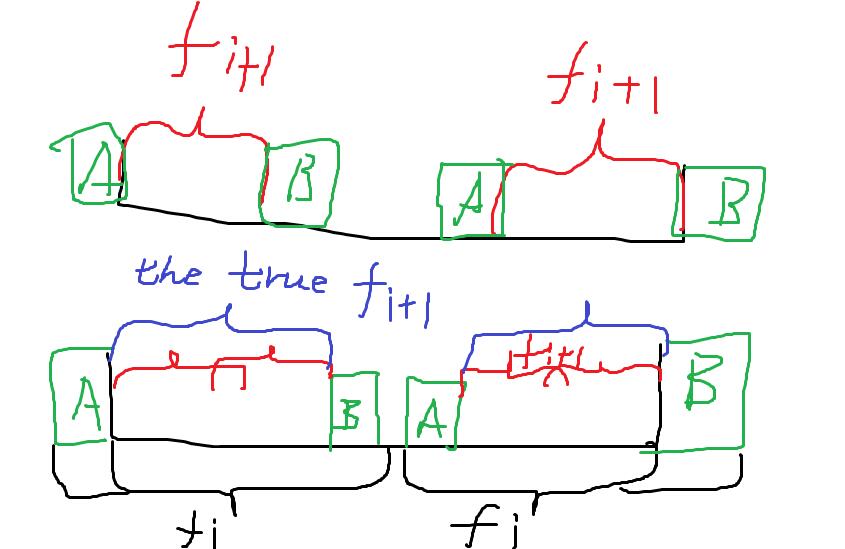
The first picture shows the situation when \(f[i]=f[i+1]+2\), and the second picture shows if \(f[i]\) (the black ones) is more than \(f[i+1]\) (the red ones) plus \(2\) , the \(f[i+1]\) must be wrong, for there's a longer border (the blue ones) of substring \([i+1, n-i-2]\).

Because of this fact, we can solve \(f[len]\) in \(O(n)\) time. We initialize \(f[i]\) as \(f[i+1]+2\), and decrease it until the substring \([i, n-i-1]\) has a border of length \(f[i]\). The proof of the complexity is similar to the one of solving \(height\) array by Suffix Array.

Code:

#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cctype>
using namespace std;

namespace zyt
{
	template<typename T>
	inline bool read(T &x)
	{
		char c;
		bool f = false;
		x = 0;
		do
			c = getchar();
		while (c != EOF && c != '-' && !isdigit(c));
		if (c == EOF)
			return false;
		if (c == '-')
			f = true, c = getchar();
		do
			x = x * 10 + c - '0', c = getchar();
		while (isdigit(c));
		if (f)
			x = -x;
		return true;
	}
	inline bool read(char *const s)
	{
		return ~scanf("%s", s);
	}
	template<typename T>
	inline void write(T x)
	{
		static char buf[20];
		char *pos = buf;
		if (x < 0)
			putchar('-'), x = -x;
		do
			*pos++ = x % 10 + '0';
		while (x /= 10);
		while (pos > buf)
			putchar(*--pos);
	}
	const int N = 1e6 + 10;
	int f[N], n;
	// f[i] is the maximum length of the border of substr[i, n - i - 1]
	char str[N];
	namespace Hash
	{
		typedef long long ll;
		typedef pair<int, int> pii;
		typedef pii hash_t;
		hash_t h[N], pow[N];
		const hash_t seed = hash_t(61, 67), p = hash_t(1e9 + 7, 1e9 + 9);
		hash_t operator + (const hash_t &a, const hash_t &b)
		{
			return hash_t((a.first + b.first) % p.first, (a.second + b.second) % p.second);
		}
		hash_t operator - (const hash_t &a, const hash_t &b)
		{
			return hash_t((a.first - b.first + p.first) % p.first,
				(a.second - b.second + p.second) % p.second);
		}
		hash_t operator * (const hash_t &a, const hash_t &b)
		{
			return hash_t(int((ll)a.first * b.first % p.first),
				int((ll)a.second * b.second % p.second));
		}
		void init()
		{
			pow[0] = make_pair(1, 1);
			for (int i = 1; i < N; i++)
				pow[i] = pow[i - 1] * seed;
		}
		inline int ctoi(const char c)
		{
			return c - 'a';
		}
		void get(const char *const s)
		{
			h[0] = make_pair(ctoi(s[0]), ctoi(s[0]));
			for (int i = 1; i < n; i++)
				h[i] = h[i - 1] * seed + make_pair(ctoi(s[i]), ctoi(s[i]));
		}
		hash_t extract(const int l, const int r)
		{
			return l ? (h[r] - h[l - 1] * pow[r - l + 1]) : h[r];
		}
	}
	using namespace Hash;
	void mk_f()
	{
		f[n >> 1] = 0;
		for (int i = (n >> 1) - 1; i >= 0; i--)
		{
			f[i] = min(f[i + 1] + 2, (n >> 1) - i);
			while (f[i] && extract(i, i + f[i] - 1) != extract(n - i - f[i], n - i - 1))
				--f[i];
		}
	}
	int work()
	{
		read(n), read(str);
		init();
		get(str);
		mk_f();
		int ans = 0;
		for (int i = 1; i <= (n >> 1); i++)
			if (extract(0, i - 1) == extract(n - i, n - 1))
				ans = max(ans, i + f[i]);
		write(ans);
		return 0;
	}
}
int main()
{
	return zyt::work();
}