【2018.8.10】四连测day4 题解

T1：给出一棵 $n$ 个节点的无根树，其中 $m$ 个节点是特殊节点，求对于任意 $i ∈ [0, m]$，包含 $i$ 个特殊节点的联通块个数$\mod 998244353$。 $1<=n,m<=1000$

输入格式

第一行包含两个正整数 $n,m$，表示树节点个数及特殊节点个数。
第二行包含 $m$ 个互不相同的正整数，表示所有特殊节点的编号。
接下来 $n$ 行，每行包含两个正整数 $u,v$，表示一条树边。

输出格式

输出包含 $m+1$ 个用空格隔开的整数，以此表示 $i=0,1,2,...,m$ 时，包含 $i$ 个特殊节点的联通块个数对 $998244353$ 取模的值。

树上连通块计数题，首先想到树形DP。

$f(i,j)$ 表示以点$i$为根的子树中，取$j$个关键点且必选根节点$i$的连通块的方案数。

那么可以发现，当考虑以$i$为根的子树的时候，我们只考虑不同子树之间合并的连通块，因为同一子树之间的连通块可以根据此原则，在子树内完成所有统计。

那具体怎么转移？又回到了子树乘法原理问题了……（不如说是树上背包）

$f(i,j) = \sum_{son_i} f(son_i,k) * f(i,j-k)　| j<=size(i), k<=j$ //size(i)表示以i为根的子树中的特殊节点数量

这转移一看就知道怎么回事了

在这之前先特判一下根节点$i$是不是特殊节点，如果是的话就把$f(i,1)$初始化为1，否则把$f(i,0)$初始化为1。

 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<vector>
 #define MAXN 131072
 #define MOD 998244353
 using namespace std;
 inline int read()
 {
     int x=; bool f=; char c=getchar();
     for(;!isdigit(c);c=getchar()) if(c=='-') f=;
     for(; isdigit(c);c=getchar()) x=(x<<)+(x<<)+(c^'');
     if(f) return x;
     return -x;
 }
 int first[],nxt[],targ[],cnte=;
 bool special[];
 int ans[];
 int dp[][],cntd[];
 int poly[];
 void AddEdge(int u,int v)
 {
     targ[cnte]=v, nxt[cnte]=first[u], first[u]=cnte++, swap(u,v);
     targ[cnte]=v, nxt[cnte]=first[u], first[u]=cnte++;
 }
 void DP(int x,int Fa)
 {
     if(special[x]) dp[x][]=, cntd[x]=;
     else dp[x][]=, cntd[x]=;
     for(int i=first[x];i;i=nxt[i])
     {
         if(targ[i]==Fa) continue;
         int y=targ[i];
         DP(y,x);
         for(int i=;i<cntd[x]+cntd[y]-;i++) poly[i]=;
         for(int i=;i<cntd[x];i++)
             for(int j=;j<cntd[y];j++)
                 (poly[i+j] += (long long)dp[x][i]*dp[y][j]%MOD) %= MOD;
         cntd[x] += cntd[y]-;
         for(int i=;i<cntd[x];i++) dp[x][i]=poly[i];
     }
     for(int i=;i<cntd[x];i++) (ans[i]+=dp[x][i])%=MOD;
     (++dp[x][])%=MOD; //一个点都不选的情况也要算上（一开始只特判了选非特殊节点的根节点）
 }
 int main()
 {
     freopen("tree.in","r",stdin);
     freopen("tree.out","w",stdout);
     int n=read(),m=read();
     for(int i=;i<m;i++) special[read()]=;
     for(int i=;i<n;i++) AddEdge(read(),read());
     DP(,);
     for(int i=;i<=m;i++) printf("%d%c",ans[i],i==m?'\n':' ');
     return ;
 }

时间复杂度根据均摊原则可知近似$O(nm)$

2018.10.1 update：这里证明了一下复杂度

T2：有 $n$ 个机器人和 $m$ 个配件，每个机器人需要若干个的配件。每个机器人对每个配件都有一定适配度，但都可互相搭配。现在请你求出，给每个机器人分配其所需数量的配件，所有机器人对其分配到的配件的适配度之和最大是多少？

输入格式

第一行包含两个正整数 $n,m$，依次表示机器人和配件个数。
第二行包含 $n$ 个正整数 $a_i$，依次表示从 $1$ 到 $n$ 号机器人所需配件数，保证 所需配件总数 $\leq m$。
接下来是一个 $n$ 行 $m$ 列的正整数矩阵 $C$，其中第 $i$ 行第 $j$ 列的数值表示，$i$ 号机器人对 $j$ 号配件的适配度。

输出格式

输出一个整数，表示答案。

$1<=n<=100, 1<=m<=200$

适配度最大值$S \leq 10^7$

不穿衣服的费用流裸题。

如此建图，从源点S到$i$号机器人连上流量为$a_i$、费用为$0$的边，从$i$号机器人到$j$号配件连上流量为$1$、费用为$C(i,j)$的边，从$i$号配件到汇点T连上流量为$1$，费用为$0$的边。这么建刚好限定了每个机器人选择配件的数量、每个配件只能被选一次，那么最大费用就是答案（注意我们平常写的是最小费用最大流！）

注意不要写EK，会被卡时成40分。

 #include<queue>
 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<iostream>
 #include<algorithm>
 #define inf 0x7f7f7f7f
 #define maxn 201
 #define maxm 401
 #define S n+m+1
 #define T n+m+2
 using namespace std;
 inline int read(){
     int x=,f=; char c=getchar();
     for(;!isdigit(c);c=getchar()) if(c=='-') f=-;
     for(;isdigit(c);c=getchar()) x=(x<<)+(x<<)+c-'';
     return x*f;
 }
 class Dinic_Enhancer
 {
 private:
     struct edge{
         int v,w,x,next; //w表示流量，x表示费用
     }e[maxm<<];
     int cnt,head[maxn];
     int depth[maxn],cur[maxn];//cur就是记录当前点u循环到了哪一条边（弧优化）
     int dis[maxn],fa[maxn],faedge[maxn];
     bool inq[maxn];
 public:
     int n,m;
     void init()
     {
         cnt=;
         memset(head,-,sizeof(head));
 
         n=read(),m=read();
         for(int i=;i<=n;i++){
             add_edge(S,i,read(),);
         }
         for(int i=;i<=n;i++)
             for(int j=;j<=m;j++) add_edge(i,n+j,,read());
 
         for(int i=n+;i<=n+m;i++) add_edge(i,T,,);
     }
     void add(int u,int v,int w,int x)
     {
         e[cnt].v=v;
         e[cnt].w=w;
         e[cnt].x=x;
         e[cnt].next=head[u];
         head[u]=cnt++;
     }
     void add_edge(int u,int v,int w,int x)
     {
         add(u,v,w,x);
         add(v,u,,-x);
     }
     bool spfa()
     {
         queue<int> Q;
         memset(depth,,sizeof(depth));
         fill(dis+,dis+T+,-inf);
         memset(inq,,sizeof inq);
         depth[S]=;
         dis[S]=;
         Q.push(S);
         int i,u;
         while(!Q.empty())
         {
             u=Q.front(); Q.pop();
             inq[u]=;
             for(i=head[u];i!=-;i=e[i].next)
                 if(dis[e[i].v]<dis[u]+e[i].x && e[i].w>)
                 {
                     dis[e[i].v]=dis[u]+e[i].x;
                     depth[e[i].v]=depth[u]+;
                     fa[e[i].v]=u, faedge[e[i].v]=i;
                     if(!inq[e[i].v]){
                         inq[e[i].v]=;
                         Q.push(e[i].v);
                        }
                 }
         }
         if(dis[T]==-inf) return ;
         return ;
     }
     int dinic()
     {
         int ans=,i,flow;
         while(spfa())
         {
             int u=T,flow=inf;
             while(u!=S) flow=min(flow,e[faedge[u]].w), u=fa[u];
             u=T;
             while(u!=S) e[faedge[u]].w-=flow, e[faedge[u]^].w+=flow, u=fa[u];
             ans+=dis[T];
         }
         return ans;
     }
 }de;
 
 int main(){
     de.init();
     printf("%d\n",de.dinic());
     return ;
 }

 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<queue>
 #define MAXN 606
 #define MAXM 40040
 using namespace std;
 inline int read()
 {
     int x=,t=,c;
     while(!isdigit(c=getchar()))if(c=='-')t=-;
     while(isdigit(c))x=x*+c-'',c=getchar();
     return x*t;
 }
 struct ZKW
 {
     int first[MAXN],targ[MAXM<<],nxt[MAXM<<],flow[MAXM<<],cost[MAXM<<],cnte=;
     int dist[MAXN],s,t,inf,ans=;
     bool inq[MAXN],vis[MAXN];
     void AddEdge(int u,int v,int l,int c)
     {
         targ[cnte]=v;flow[cnte]=l;cost[cnte]=c;nxt[cnte]=first[u];first[u]=cnte++;swap(u,v);
         targ[cnte]=v;flow[cnte]=;cost[cnte]=-c;nxt[cnte]=first[u];first[u]=cnte++;
     }
     bool SPFA()
     {
         memset(dist,,sizeof dist);
         memset(&inf,,sizeof(int));
         memset(inq,,sizeof inq);
         queue<int> Q;
         dist[t]=;
         inq[t]=;
         Q.push(t);
         while(!Q.empty())
         {
             int x=Q.front();Q.pop();inq[x]=;
             for(int i=first[x];i;i=nxt[i])
             {
                 if(flow[i^]&&dist[targ[i]]>dist[x]-cost[i])
                 {
                     dist[targ[i]]=dist[x]-cost[i];
                     if(!inq[targ[i]])
                     {
                         Q.push(targ[i]);
                         inq[targ[i]]=;
                     }
                 }
             }
         }
         return dist[s]!=inf;
     }
     int DFS(int x,int maxflow)
     {
         if(x==t||!maxflow){ans+=dist[s]*maxflow;return maxflow;}
         if(vis[x])return ;
         vis[x]=;
         int ret=,f;
         for(int i=first[x];i&&maxflow;i=nxt[i])
         {
             if(dist[targ[i]]==dist[x]-cost[i])
             {
                 if(f=DFS(targ[i],min(maxflow,flow[i])))
                 {
                     ret+=f;
                     flow[i]-=f;
                     flow[i^]+=f;
                     maxflow-=f;
                 }
             }
         }
         vis[x]=;
         return ret;
     }
     int solve(int source,int tank)
     {
         s=source;t=tank;int Flow=;
         while(SPFA())
         {
             Flow+=DFS(s,);
         }
         return Flow;
     }
 }zkw;
 int n,m;
 int main()
 {
     freopen("robot.in","r",stdin);
     freopen("robot.out","w",stdout);
     n=read();m=read();
     for(int i=;i<=n;i++)zkw.AddEdge(i+,,read(),);
     for(int i=;i<=n;i++)
         for(int j=;j<=m;j++)
             zkw.AddEdge(n++j,i+,,-read());
     for(int j=;j<=m;j++)
         zkw.AddEdge(,n++j,,);
     zkw.solve(,);
     printf("%d",-zkw.ans);
     return ;
 }

T3：有一维空间内 $n$ 个点，编号从 $1$ 到 $n$，编号为 $i$ 的点坐标为 $x_i$。现在，请选出编号连续的一些点，使得被选出的所有点到某一点的距离和的最小值不超过一正整数 $m$，问最多能选出多少点？

输入格式

第一行，包含两个正整数 $n,m$，依次表示点数和距离和限制。
第二行，包含 $n$ 个正整数 $x_i$，依次表示每个点的坐标。
输出格式

输出共一行，表示最多选取点数。

$1<=n<=10^5, 1<=m<=10^9, 1<=x_i<=10^6$

难度堪比提高组D2T3

第一眼看到这题，不会，于是想想暴力做法。

首先我们得知道这样一个幼儿园知识：n个数中，与这n个数的差的绝对值（在空间意义里就是距离）之和最小的数 是这n个数的中位数。

为什么？简单证明：

把这n个数从小到大排序。假设我们先认为与这n个数的差的绝对值（在空间意义里就是距离）之和（下面都称之为答案）是最小的数（第一个数），我们把答案改为第二个数，则从第1个数到第2个数的距离会增加$dis(1,2)$，第2~n个数到第2个数的距离都会减少$dis(1,2)$，那么很明显距离减少的比增加的多，距离总和也会减少。把答案从第二个数改为第三个数，再改为第四个数……一直改到中位数为止，距离减少的都比增加的多（距离减少的占一半以上），所以距离总和不断减少；而从中位数改到比中位数大的下一位时，距离增加的数就超过一半了，而距离减少的数随之少于一半，且之后距离增加的数会越来越多，这时距离总和就会不断增加。

总结一下，就是 总距离随数的排名的变化 的图像是单峰下凸的，且排名在最中间（中位数）时所有数到它的总距离最小。大家可以手动写个数列验证一下。

下面回到正题：

用两重循环枚举所有选点区间（按编号顺序），搜一遍区间里的点找出中间点（可以理解为n个坐标的中位数）并暴力求解所有被选点到它的总距离就可以了。

这样的复杂度是$O(n^3)$，可以过40%的数据。

我们很快发现最外层的两重循环枚举区间可以优化。这样想：一个选点区间的所有数到该区间中位数的距离总和不超过$m$的话，那更短的区间到其中位数的距离总和一定也能不超过$m$（至少把满足条件的选点区间中去掉头或尾一个点的情况就可以，总距离只会减少那个点到中位数的距离，不会增加，因此依然可以不超过$m$）。因此区间答案随区间长度单调递减，把其中一重枚举区间长度的循环改为二分即可。

这样的复杂度是$O(n^2 \log n)$。

到了这里简单的优化已经不能影响复杂度了，因此开始考虑数据结构。你很惊奇地发现$x_i \leq 10^6$，坐标值这么小肯定可以入手啊！结合数轴的背景，我们可以用值域线段树（权值线段树）/平衡树优化辣！

$10^6$大小的值域线段树的做法就是先把开头区间的坐标值都插进去，之后每次移动选点区间其实只会删去开头的坐标值，并插入结尾后的一个新坐标值，这样分析的话每个坐标值最多只会被插入一次和删去一次，插入的复杂度可控制在$O（n \log x_i）$内。然后对于每个区间，在当时的权值线段树中跑一边树，从根遍历到中位数所在叶子节点即可，每次找中位数的复杂度可控制在$O(\log x_i)$里。

然而找出了中位数好像还得暴力求每个点到这个中位数的距离啊？！

你又惊奇地发现，其实每个点到中位数的距离之和相当于如图的橙色线条长度之和

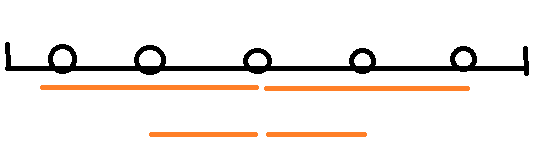
它相当于 坐标轴总长 减去 中位数前每个坐标到坐标轴起点的距离（坐标值）的和 再减去  中位数后每个坐标到坐标轴终点的距离的和。

借助上面那个值域线段树，维护每个区间内所有数 到坐标轴起点的距离之和 以及 到坐标轴终点的距离之和 即可。然后通过上述计算得到当前选点区间内所有坐标到中位数的距离。

加上外层套的二分区间长度，这样的复杂度是$O（n \log n \log x_i）$。

丧心病狂的出题人为了卡$log^2$的常数，临考试结束的时候临时取消了这题的氧气优化，然而这个复杂度好像还是能卡过

正解是$O(n \log x_i)$的。其实最后这步优化很简单，把二分区间长度套枚举起点 改为滑动窗口即可。根据上述区间答案随区间长度单调递减这个推论，从第一个点开始，当滑动窗口右端点右移到不满足条件（区间内的被选点到中位数的距离和超过 $m$）时，右移左端点缩小区间即可。滑动窗口枚举区间的复杂度是$O(n)$的，答案就是窗口长度的最大值。）

这是值域线段树做法，如果把值域线段树改成平衡树也可以维护这些，树可以只开$n$位，但是平衡树常数大，容易被卡成狗……

 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #define MAXN 1048576
 using namespace std;
 inline long long read()
 {
     long long x=,t=;int c;
     while(!isdigit(c=getchar()))if(c=='-')t=-;
     while(isdigit(c))x=x*+c-'',c=getchar();
     return x*t;
 }
 int n;
 long long m;
 int x[MAXN];
 int size[<<];
 long long sumv[<<];
 void maintain(int o,int L,int R)
 {
     int m=L+R>>,lc=o<<,rc=lc|;
     size[o]=size[lc]+size[rc];
     sumv[o]=sumv[lc]+sumv[rc];
 }
 void Add(int o,int L,int R,const int pos,const int v)
 {
     if(L==R)
     {
         size[o]+=v;
         sumv[o]=(long long)size[o]*L;
     }
     else
     {
         int m=L+R>>,lc=o<<,rc=lc|;
         if(pos<=m)Add(lc,L,m,pos,v);
         else Add(rc,m+,R,pos,v);
         maintain(o,L,R);
     }
 }
 int GetKthPos(int o,int L,int R,const int k)
 {
     if(L==R)
     {
         return L;
     }
     else
     {
         int m=L+R>>,lc=o<<,rc=lc|;
         if(size[lc]>=k)return GetKthPos(lc,L,m,k);
         else return GetKthPos(rc,m+,R,k-size[lc]);
     }
 }
 long long toLeft(int o,int L,int R,const int ql,const int qr)
 {
     if(ql<=L&&R<=qr)
     {
         return sumv[o]-(long long)size[o]*ql;
     }
     else
     {
         int m=L+R>>,lc=o<<,rc=lc|;
         long long size=;
         if(ql<=m)size+=toLeft(lc,L,m,ql,qr);
         if(m<qr)size+=toLeft(rc,m+,R,ql,qr);
         return size;
     }
 }
 long long toRight(int o,int L,int R,const int ql,const int qr)
 {
     if(ql<=L&&R<=qr)
     {
         return (long long)size[o]*qr-sumv[o];
     }
     else
     {
         int m=L+R>>,lc=o<<,rc=lc|;
         long long size=;
         if(ql<=m)size+=toRight(lc,L,m,ql,qr);
         if(m<qr)size+=toRight(rc,m+,R,ql,qr);
         return size;
     }
 }
 long long CountPrice(int size)
 {
     int mid=GetKthPos(,,,(size+)>>);
     long long ret=;
     ret+=toRight(,,,,mid);
     ret+=toLeft(,,,mid,);
     return ret;
 }
 int main()
 {
     freopen("choose.in","r",stdin);
     freopen("choose.out","w",stdout);
     n=read();m=read();
     for(int i=;i<=n;i++)x[i]=read();
     int L=,R=,ans=;
     for(R=;R<=n;R++)
     {
         Add(,,,x[R],);
         while(CountPrice(R-L+)>m)
             Add(,,,x[L++],-);
         ans=max(ans,R-L+);
     }
     printf("%d",ans);
     return ;
 }

总而言之，题出的不错，就是题面写错数据卡常低分罚跑圈应该吐槽吐槽