bzoj 2132 圈地计划【最小割+dinic】

对于网格图，尤其是这种要求相邻各自不同的，考虑黑白染色

对于这张染色后图来说：



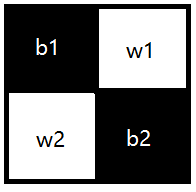
对于每个黑格：

• 表示初始时选择商业区；
• s点向它连商业区收益的流量，它向t点连工业区收益的流量；
• 割断S侧的边说明反悔，则保留T侧边的边权（工业区），割断T侧的边说明维持原样，保留S侧边权（商业区）

对于每个白格：

• 表示初始时选择工业区；
• s点向它连工业区收益的流量，它向t点连商业区收益的流量；
• 割断S侧的边说明反悔，则保留T侧边的边权（商业区），割断T侧的边说明维持原样，保留S侧边权（工业区）

对于相邻格子：

• 相邻黑白格子间连区域不同收益的流量，双向边（注意是这两个格子的c值和）
• 如果相邻两个点被划入同侧，则它们中间的边不会被割，收益被保留；如果被划入异侧，则中间边被割断，收益被减掉

\(ans = sum- 最小割\) （注意这里的sum是对于每个周边有k个格子的格子(i,j)，算上c[i][j]*k）

建图：

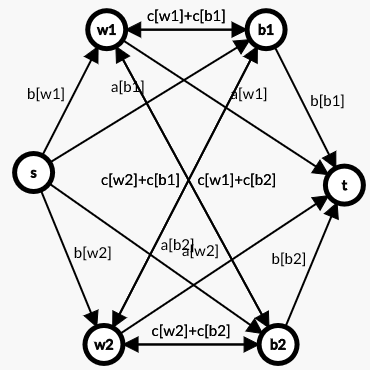
#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
using namespace std;
const int N=105,E=1000005,inf=1e9,dx[]={1,-1,0,0},dy[]={0,0,-1,1};
int n,m,a[N][N],b[N][N],c[N][N],id[N][N],s,t,sum,h[E],cnt=1,le[E];
struct qwe
{
	int ne,to,va;
}e[E<<1];
int read()
{
	int r=0,f=1;
	char p=getchar();
	while(p>'9'||p<'0')
	{
		if(p=='-')
			f=-1;
		p=getchar();
	}
	while(p>='0'&&p<='9')
	{
		r=r*10+p-48;
		p=getchar();
	}
	return r*f;
}
void add(int u,int v,int w)
{
	cnt++;
	e[cnt].ne=h[u];
	e[cnt].to=v;
	e[cnt].va=w;
	h[u]=cnt;
}
void ins(int u,int v,int w)
{
	add(u,v,w);
	add(v,u,0);
}
bool bfs()
{
	queue<int>q;
	memset(le,0,sizeof(le));
	le[s]=1;
	q.push(s);
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		for(int i=h[u];i;i=e[i].ne)
			if(!le[e[i].to]&&e[i].va>0)
			{
				le[e[i].to]=le[u]+1;
				q.push(e[i].to);
			}
	}
	return le[t];
}
int dfs(int u,int f)
{
	if(u==t||!f)
		return f;
	int us=0;
	for(int i=h[u];i&&us<f;i=e[i].ne)
		if(le[u]+1==le[e[i].to]&&e[i].va>0)
		{
			int t=dfs(e[i].to,min(e[i].va,f-us));
			e[i].va-=t;
			e[i^1].va+=t;
			us+=t;
		}
	if(!us)
		le[u]=0;
	return us;
}
int dinic()
{
	int re=0;
	while(bfs())
		re+=dfs(s,inf);
	return re;
}
int main()
{
	n=read(),m=read();
	t=n*m+1;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			a[i][j]=read(),sum+=a[i][j];
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			b[i][j]=read(),sum+=b[i][j];
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
		{
			c[i][j]=read();
			int t=0;
			for(int k=0;k<4;k++)
				if(i+dx[k]>=1&&i+dx[k]<=n&&j+dy[k]>=1&&j+dy[k]<=m)
					t++;
			sum+=c[i][j]*t;
		}
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			id[i][j]=(i-1)*m+j;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
		{
			if((i+j)%2==1)
			{
				ins(s,id[i][j],a[i][j]);
				ins(id[i][j],t,b[i][j]);
			}
			else
			{
				ins(s,id[i][j],b[i][j]);
				ins(id[i][j],t,a[i][j]);
			}
			// for(int k=0;k<4;k++)
				// if(i+dx[k]>=1&&i+dx[k]<=n&&j+dy[k]>=1&&j+dy[k]<=m)
					// ins(id[i][j],id[i+dx[k]][j+dy[k]],c[i][j]+c[i+dx[k]][j+dy[k]]);
			if(i!=n)
			{
				add(id[i][j],id[i+1][j],c[i][j]+c[i+1][j]);
				add(id[i+1][j],id[i][j],c[i][j]+c[i+1][j]);
			}
			if(j!=m)
			{
				add(id[i][j],id[i][j+1],c[i][j]+c[i][j+1]);
				add(id[i][j+1],id[i][j],c[i][j]+c[i][j+1]);
			}
		}
	printf("%d\n",sum-dinic());
	return 0;
}