Java数据结构和算法(二)--队列

上一篇文章写了栈的相关知识，而本文会讲一下队列

队列是一种特殊的线性表，在尾部插入(入队Enqueue)，从头部删除(出队Dequeue)，和栈的特性相反，存取数据特点是：FIFO

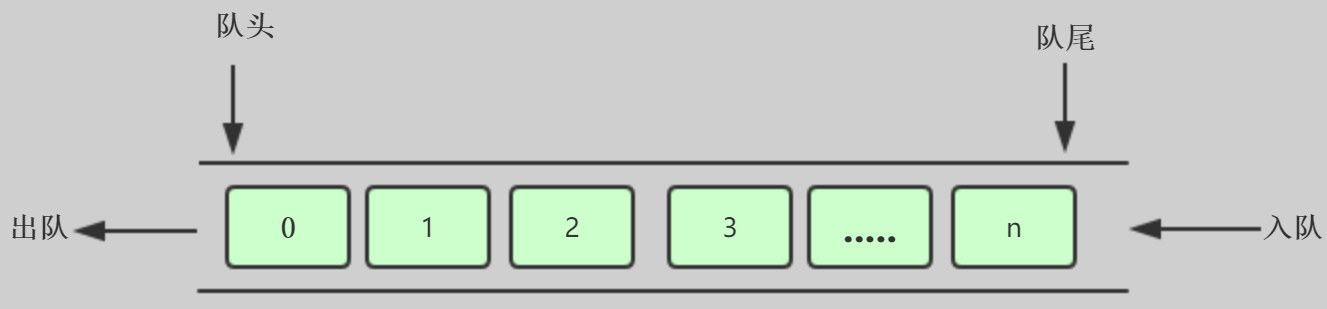
Java中queue源码：

public interface Queue<E> extends Collection<E> {

    boolean add(E e);    //添加一条数据到队尾，成功返回true，否则false

    boolean offer(E e);	//添加一条数据到队尾，如果队列满了，会返回null

    E remove();	//从队头删除一条数据，如果是空队列，会发生异常

    E poll();	//从队头删除一条数据，如果是空队列，会返回null

    E element();	//返回队头的数据，如果是空队列，会发生异常

    E peek();	//返回队头的数据，如果是空队列，会返回null
}

queue直接继承Collection，有6个基本方法实现增删查的功能

单向队列：

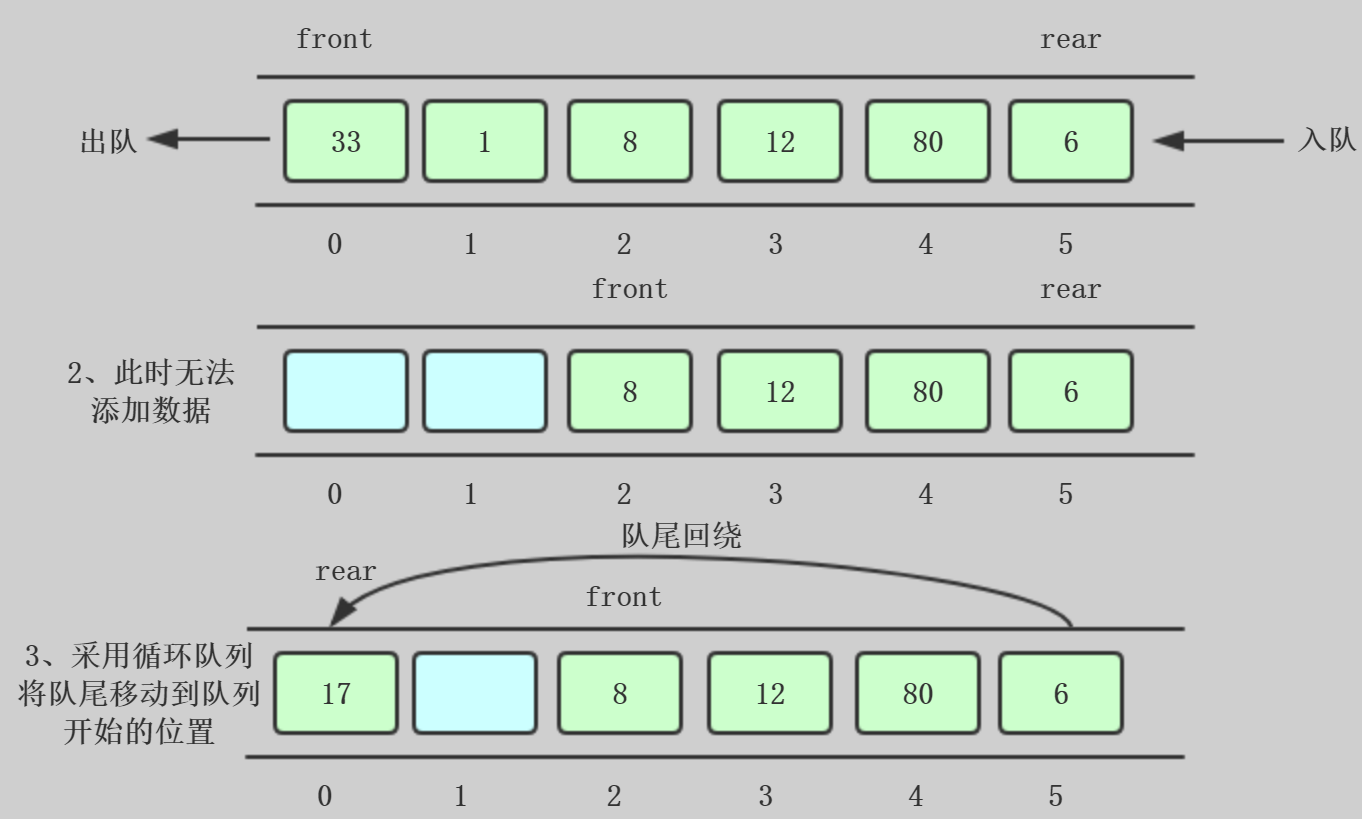
PS：删除的数据还是保存在内存中的，只是不能被访问，因为front位置移动了

上图中第二步，我们从队头front删除一些数据，然后队尾由于插入数据，rear移动到最后，此时无法插入数据

为了避免队列不满但是不能插入数据的情况，采用第三步：循环队列，将队尾回绕到队列开始的位置

Java代码实现单向队列：

public class MyQueue<E> {
    private int maxSize;    //队列总大小
    private Object[] elementData;   //保存数据的数组
    private int front;  //队头
    private int rear;   //队尾
    private int nItems; //队列元素的数量

    public MyQueue(int value) {
        maxSize = value;
        elementData = new Object[value];
        front = 0;
        rear = -1;
        nItems = 0;
    }

    public void add(E e) {
        if (isFull()) {
            System.out.println("当前队列已满");
        } else {
            if (rear == maxSize - 1) {  //如果rear已经指向最后面，将队尾回绕到队列开始的位置
                rear = -1;
            }
            elementData[++rear] = e;    //rear后移一位(首位为0)，并且插入数据
            nItems++;   //元素数量+1
        }
    }

    //移除数据
    public E remove(){
        E temp = null;
        if (isEmpty()) {
            System.out.println("当前为空队列，无法删除");
        } else {
            temp = (E)elementData[front++];   //返回队头front的数据，然后front后移一位
            if (front == maxSize) { //如果front已经后移到最末尾了，front重置
                front = 0;
            }
            nItems--;   //元素数量-1
        }
        return temp;
    }

    public E peek(){   //查看队头数据
        return (E)elementData[front];
    }

    public boolean isFull(){
        return (nItems == maxSize);
    }

    public boolean isEmpty(){
        return (nItems ==0);
    }

    public int getSize(){   //返回队列的大小
        return nItems;
    }
}

public static void main(String[] args) {
	MyQueue<Integer> queue = new MyQueue<>(5);
	int i = 0;
	while (!queue.isFull()) {
		queue.add(i++);
	}
	queue.add(6);	//当前队列已满，无法添加了
	while (!queue.isEmpty()) {
		queue.remove();
	}
}

输出结果：当前队列已满

优先级队列：

　　优先级队列是比栈和队列更专用的数据结构，一般情况下，和浦东队列一样，优先级队列有一个头部和一个尾部，也是从头部移除数据。

不过优先级队列中，元素按照关键字是有序的。关键字最小的元素总是在头部，元素在插入的时候按照顺序插入到合适的位置以确保队列的顺序

　　优先级队列在程序中也有很多应用，例如：图的最小生成树

　　这里我们使用简单数组实现优先级队列，这种方式比较慢，但是很简单。优先级队列一般都是通过队来实现，在后面会降到

代码实现：

public class MyPriorityQueue  {

    private int maxSize;    //队列总大小
    private Object[] elementData;   //保存数据的数组
    private int nItems; //队列元素的数量

    public MyPriorityQueue(int value) {
        maxSize = value;
        elementData = new Object[value];
        nItems = 0;
    }

    public boolean add(int e) {　　//添加元素，关键字小的元素在头部，通过插入排序实现
        int j;
        if (nItems == 0) {
            elementData[nItems++] = e;
        } else {
                j = nItems - 1;
                while (j >= 0 && e > (int)elementData[j]) {
                    elementData[j+1] = elementData[j];
                    j--;
                }
                elementData[j+1] = e;
            nItems++;
        }
        return true;
    }

    //移除数据
    public Object remove(){　　//删除一条数据，返回老数据
        Object value = elementData[nItems-1];
        elementData[nItems-1] = null;
        nItems--;
        return value;
    }

    public Object peekMin() {　　//返回优先级最高的元素
        return elementData[nItems-1];
    }

    //判断是否为空
    public boolean isEmpty(){
        return (nItems == 0);
    }

    //判断是否满了
    public boolean isFull(){
        return (nItems == maxSize);
    }
}

public static void main(String[] args) {
	MyPriorityQueue queue = new MyPriorityQueue(5);
	int i = 0;
	while (!queue.isFull()) {
		queue.add(i++);
	}
	while (!queue.isEmpty()) {
		System.out.println(queue.peekMin());;
		queue.remove();
	}
}

打印结果：
0
1
2
3
4

add()通过插入排序实现，时间复杂度O(N)，如果忘记插入排序，可以参考：Java数据结构和算法(三)--三大排序--冒泡、选择、插入排序

PS：Queue一般作为程序的某种实现，而不是用来保存数据

内容参考：<Java数据结构和算法>