subgradients

目录

• 定义
  • 上镜图解释
• 次梯度的存在性
• 性质
  • 极值
  • 非负数乘 \(\alpha f(x)\)
  • 和，积分，期望
  • 仿射变换
  • 仿梯度
  • 混合函数
• 应用
  • Pointwise maximum
  • 上确界 supremum
  • Minimization over some variables
  • 拟凸函数

《Subgradients》
Subderivate-wiki
Subgradient method-wiki
《Subgradient method》
Subgradient-Prof.S.Boyd,EE364b,StanfordUniversity
《Characterization of the Subdifferential of Some Matrix Norms 》

定义

我们称\(g \in \mathbb{R}^n\)是\(f:\mathbb{R}^{n} \rightarrow \mathbb{R}\)在\(x\in domf\)的次梯度，如果对于任意的\(z \in domf\)，满足：
\[
f(z) \ge f(x) + g^T(z-x)
\]
如果\(f\)是可微凸函数，那么\(g\)就是\(f\)在\(x\)处的梯度。我们将\(z\)看成变量，那么仿射函数\(f(x)+g^T(z-x)\)是\(f(z)\)的一个全局下估计。这个次梯度的作用，就是在处理不可微函数的时候，提供一个替代梯度的工具，而且，根据定义，沿着次梯度方向，函数的值是非降的：
\[
f(\alpha g+x) \ge f(x) + \alpha g^Tg
\]
另外，如果极限存在，有下面的性质，这联系了方向导数和次梯度：
\[
\lim \limits_{z \rightarrow x^+} \frac{f(z)-f(x)}{\|z-x\|} \ge g^T(z-x)/\|z-x\|
\]
当然，还有从左往右的来的，这里就不讲了。

下图是一个例子，我们可以看到，在存在梯度的地方，次梯度就是梯度，在不可导的地方，次梯度是一个凸集。

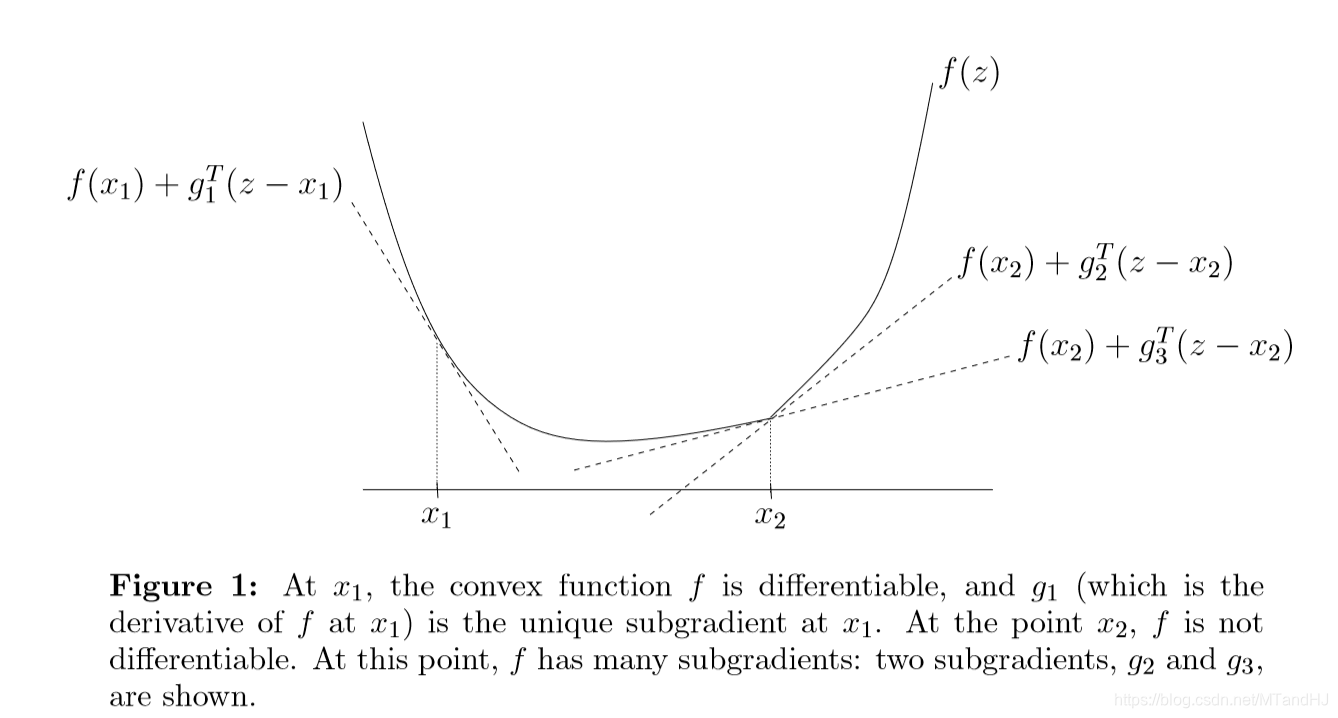
次梯度总是闭凸集，即便\(f\)不是凸函数，有下面的性质：
\[
\partial f(x) = \bigcap \limits_{z \in domf} \{ g| f(z) \ge f(x) + g^T (z-x) \}
\]

下面是\(f(x) = |x|\)的例子：

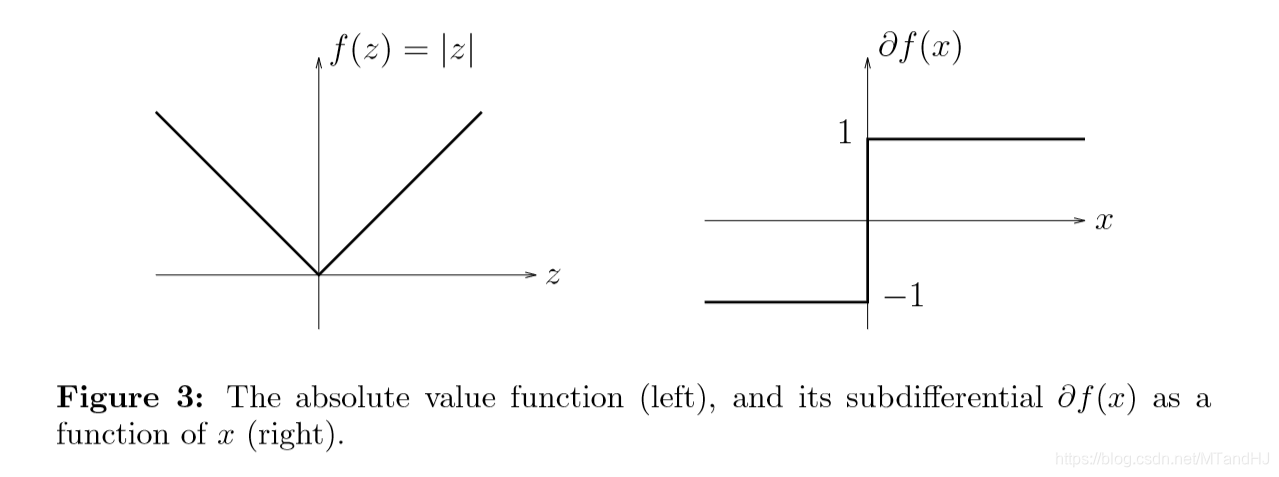
上镜图解释

\(g\)是次梯度，当且仅当\((g, -1)\)是\(f\)的上镜图在\((x, f(x))\)处的一个支撑超平面。

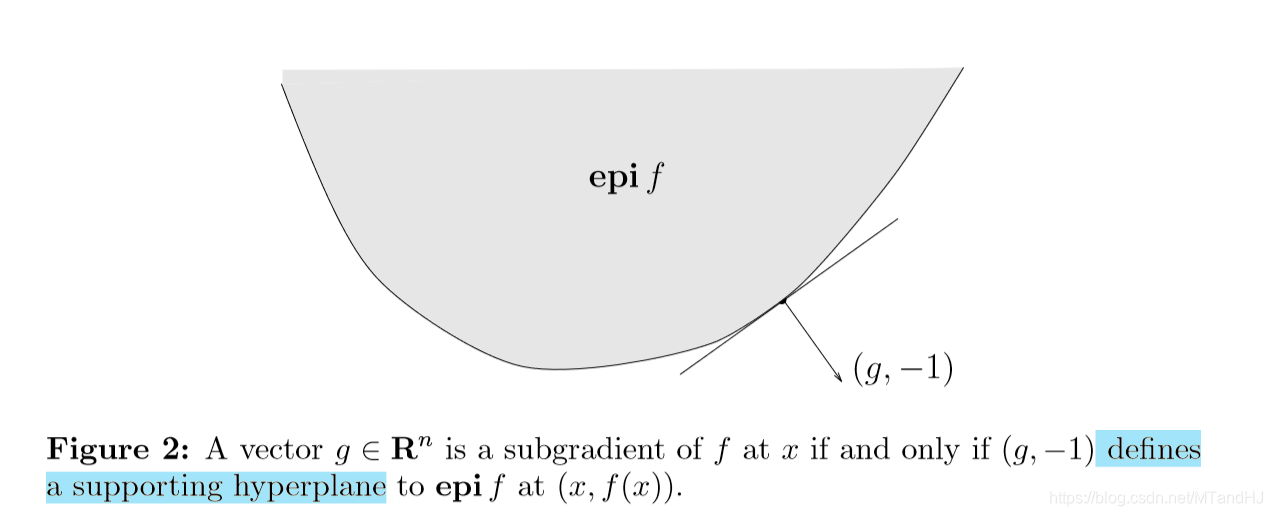
函数\(f\)的上镜图定义为：
\[
\mathbf{epi} f = \{ (x, t) | x \in \mathbf{dom} f, f(x) \le t\}
\]

一个函数是凸函数，当且仅当其上镜图是凸集。

我们来证明一开始的结论，即\(g\)是次梯度，当且仅当\((g, -1)\)是\(f\)的上镜图在\((x, f(x))\)处的一个支撑超平面。
首先，若\((g, -1)\)是\(f\)的上镜图在\((x, f(x))\)处的一个支撑超平面，则：
\[
g^T(x-x_0)-(t-f(x_0)) \le 0 \\
\Rightarrow t \ge f(x_0)+g^T(x-x_0)
\]
对所有\((x, t) \in \mathbf{epi} f\)成立，令\(t=f(x)\)，结果便得到。
反过来，如果\(g\)是次梯度，那么：
\[
f(z) \ge f(x) + g^T(z-x) \\
\Rightarrow f(z)-f(x) \ge g^T(z-x)
\]
又\(t \ge f(z), (z, t) \in \mathbf{epi} f\),所以：
\[
t - f(x)\ge f(z)-f(x) \ge g^T(z-x)
\]
所以，\((g,-1)\)在\((x, f(x))\)处定义了一个超平面。

次梯度的存在性

如果\(f\)是凸函数，且\(x \in \mathbf{int} \mathbf{dom} f\)，那么\(\partial f(x)\)非空且闭。根据支撑超平面定理，我们知道，在\((x, f(x))\)处存在关于\(\mathbf{epi} f\)的一个超平面，设\(a \in \mathbb{R}^n, b \in \mathbb{R}\)，则对于任意的\((z, t)\in \mathbf{epi} f\)都有：

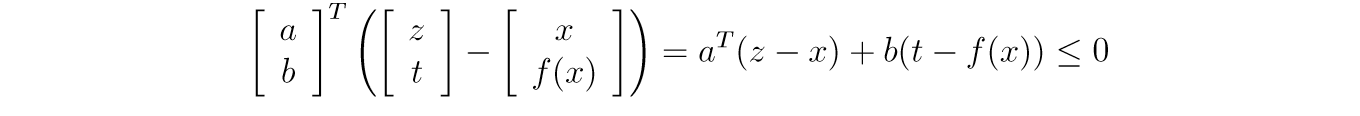
显然，\((x, f(x)+\epsilon)\)也符合条件，这意味着\(b\le0\)，以及：
\[
a^T(z-x)+b(f(z) - f(x)) \le 0
\]
对所有\(z\)成立。
如果\(b=0\)，那么\(a=0\)，不构成超平面，即\(b < 0\)。
于是：
\[
f(z) \ge f(x) +-a^T/b(z-x)
\]
即\(-a/b \in \partial f(x)\)

性质

极值

\(x^*\)是凸函数\(f(x)\)的最小值，当且仅当\(f\)在\(x^*\)处存在次梯度且
\[
0 \in \partial f(x^*)
\]
\(f(x) \ge f(x^*) \Rightarrow 0 \in \partial f(x^*)\)

非负数乘 \(\alpha f(x)\)

\(\partial(\alpha f) = \alpha \partial f, \alpha \ge 0\)

和，积分，期望

\(f = f_1+f_2\ldots+f_n\)，\(f_i,i=1,2,\ldots,m\)均为凸函数，那么：
\[
\partial f=\partial f_1 +\partial f_2 + \ldots +\partial f_n
\]
\(F(x)= \int_Y f(x,y) dy\), 固定\(y\), \(f(x,y)\)为凸函数，那么：
\[
\partial F(x)=\int_Y \partial_x f(x,y) dy
\]
\[
f(z,y) \ge f(x,y)+g^T(y)(z-x) \\
\Rightarrow \int_Yf(z,y)dy \ge \int_Yf(x,y)dy+\int_Yg^T(y)dy(z-x)
\]
不过需要注意的一点是，这里的等号都是对于特定的次梯度，我总感觉\(f\)的次梯度的集合不止于此，或许会稍微大一点？就是对于和来讲，下面这个式子成立吗？：
\[
\partial f=\{ g_1+g_2+\ldots + g_n| g_1\in \partial f_1, \ldots, g_n\in \partial f_n\}
\]
至少凸函数没问题吧，凸函数一定是连续函数，且左右导数存在，那么\(g\)的范围都是固定的。

仿射变换

\(f(x)\)是凸函数，令\(h(x)=f(Ax+b)\)则：
\[
f(Az+b) \ge f(Ax+b)+g^T(Az+b-Ax-b) \\
\Rightarrow h(z) \ge h(x)+ (A^Tg)^T(z-x) \\
\Rightarrow \partial h(x)=A^T\partial f(Ax+b)
\]

仿梯度

我们知道梯度有下面这些性质：
\[
\nabla c = 0\\
\nabla (\varphi \pm \psi) = \nabla \varphi \pm \nabla \psi \\
\nabla(c\varphi) = c \nabla \varphi \\
\nabla (\frac{\varphi}{\psi})= \frac{\psi \nabla \varphi - \varphi \nabla \psi}{\psi^2} \\
\nabla f(\varphi) = f'(\varphi) \nabla \varphi \\
\]

我认为（注意是我认为！！！大概是是异想天开。）\(f\)为凸函数的时候，或者\(f\)为可微（这个时候是一定的）的时候，上面的性质也是存在的。当然，这只是针对某些次梯度。因为当\(f\)为凸函数的时候，\(f\)的左右导数都存在，那么：
\[
k_+:=\lim \limits_{t \rightarrow 0^+} \frac{f(x+te_k)-f(x)}{t}
\]
那么（凸函数的性质）
\[
f(x+te_k)-f(x) \ge tk_+=(k_+e_k)^T(te_k), t>0
\]
同理：
\[
k_-:=\lim \limits_{t \rightarrow 0^-} \frac{f(x+te_k)-f(x)}{t}
\]
\[
f(x+te_k)-f(x) \ge tk_-=(k_-e_k)^T(te_k), t<0
\]
而且\(k_- \le k_+\)。
事实上，因为：
\[
\frac{f(x+te_k)-f(x)}{t} \ge k_+ \ge k_- \ge \frac{f(x)-f(x-te_k)}{t},t>0
\]
所以，容易证明：
\[
f(x+te_k) \ge f(x) + (\lambda_1k_+ + (1-\lambda_1)k_-)e_k^Tte_k, 0 \le \lambda_1 \le 1
\]
容易验证\(h(t) = f(x+tv)\)时关于\(t\)的凸函数，那么：
\[
K_v^+ := \lim \limits_{t \rightarrow 0^+} \frac{h(t)-h(0)}{t\|v\|}
\]
同理
\[
K_v^- := \lim \limits_{t \rightarrow 0^-} \frac{h(t)-h(0)}{t\|v\|}
\]
一样的分析，我们可以知道：
\[
f(x+tv) \ge f(x) + \frac{(\lambda K_v^+ + (1-\lambda )K_v^-)}{\|v\|} v^Ttv, 0 \le \lambda \le 1
\]
不好意思，证到这里我证不下去了，我实在不知道结果该是什么。

混合函数

应用

Pointwise maximum

\[
f(x)=\max \limits_{i=1,2,\ldots,m} f_i(x)
\]
其中\(f_i,i=1,2,\ldots,m\)为凸函数。

\(\mathbf{Co}(\cdot)\)大概是把里面的集合凸化（我的理解）：
\[
\mathbf{Co}(\mathcal{S})=\{ \lambda g_1+(1-\lambda) g_2| g_1,g_2\in \mathcal{S},\lambda \in [0,1]\}
\]

第一个例子，可微函数取最大：

我倒觉得蛮好理解的，因为\(\nabla_i f(x)\)和\(\nabla_j f(x)\)如果都是次梯度，那么根据次梯度的集合都是凸集可以知道\(\nabla_i f(x),\nabla_j f(x)\)的凸组合也是次梯度。

第二个例子，\(\ell_1\)范数：

我也觉得蛮好理解的。

上确界 supremum

\[
f(x) = \sup \limits_{\alpha \in \mathcal{A}} f_\alpha (x)
\]
\(f_\alpha (x)\)是次可微的。

例子，最大特征值问题：

Minimization over some variables

拟凸函数