[BZOJ]1076 奖励关(SCOI2008)

　　终于又一次迎来了一道期望DP题，按照约定，小C把它贴了出来。

Description

　　你正在玩你最喜欢的电子游戏，并且刚刚进入一个奖励关。在这个奖励关里，系统将依次随机抛出k次宝物，每次你都可以选择吃或者不吃（必须在抛出下一个宝物之前做出选择，且现在决定不吃的宝物以后也不能再吃）。宝物一共有n种，系统每次抛出这n种宝物的概率都相同且相互独立。也就是说，即使前k-1次系统都抛出宝物1（这种情况是有可能出现的，尽管概率非常小），第k次抛出各个宝物的概率依然均为1/n。获取第i种宝物将得到Pi分，但并不是每种宝物都是可以随意获取的。第i种宝物有一个前提宝物集合Si。只有当Si中所有宝物都至少吃过一次，才能吃第i种宝物（如果系统抛出了一个目前不能吃的宝物，相当于白白的损失了一次机会）。注意，Pi可以是负数，但如果它是很多高分宝物的前提，损失短期利益而吃掉这个负分宝物将获得更大的长期利益。假设你采取最优策略，平均情况你一共能在奖励关得到多少分值？

Input

　　第一行为两个正整数k和n，即宝物的数量和种类。以下n行分别描述一种宝物，其中第一个整数代表分值，随后的整数依次代表该宝物的各个前提宝物（各宝物编号为1到n），以0结尾。

Output

　　输出一个实数，保留六位小数，即在最优策略下平均情况的得分。

Sample Input

　　1 2
　　1 0
　　2 0

Sample Output

　　1.500000

HINT

　　1<=k<=100，1<=n<=15，分值为[-10^6,10^6]内的整数。

Solution

　　关于概率期望的题目让人头大，但是如果你还记得之前的口诀“概率正着做，期望倒着做”，这题就会变得很无脑。

　　很显然这题要我们求的是期望，所以我们倒着开始思考问题。

　　我们注意到n的范围小等于15，那还能是什么做法啊，当然是状压啊。

　　于是我们考虑设计状态，f[i][j]表示取了已经抛出i次物品，并且取了集合为j的物品至少1次，这之后按照最优策略能取到的期望值。

　　所谓最优策略，实际上就是比较转移代价和目标收益之间的大小关系，

　　假设我们在状态f[i][j]，假设可以取得物品x，我们就要斟酌一下取得x的代价和取得x之后的收益，

　　也就是比较-w[x]和f[i+1][j|ys[x]]的大小，

　　如果-w[x]<f[i+1][j|ys[x]]，也就是说收益更大，按照最优原则我们应该要取；（为什么是“应该”呢）

　　反之就是代价更大，按照最优原则我们肯定不能取，但是请注意，不取x也有一个收益，那就是f[i+1][j]。

　　不过就算取x的收益比代价大，但这两者的差值不一定大于不取x的收益，所以按照最优策略还是要对两者取一个max。

　　结合上面的思路来看，我们发现f[i][j]永远不可能是负数。

　　前面说的是能够取得物品x的情况，那么什么时候取不了物品x（未满足x的前提宝物集合）呢？

　　这种问题还用问？看看你自己设计的状态就知道了吧。

　　转移方程：，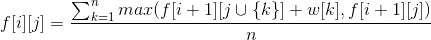

　　其中如果取不了物品k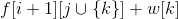，用 0 代替。

　　时间复杂度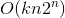，虽然复杂度有5亿然而却跑得飞快。

#include <cstdio>

#include <algorithm>

#include <cstring>

#define MS 17

#define MN 35005

using namespace std;

int ys[MS],w[MS],prt[MS];

double f[][MN];

int m,n,stp;

inline int read()

{

    int n=,f=; char c=getchar();

    while (c<'' || c>'') {if(c=='-')f=-; c=getchar();}

    while (c>='' && c<='') {n=n*+c-''; c=getchar();}

    return n*f;

}

int main()

{

    register int i,j,k,x,lg,rg;

    m=read(); n=read();

    for (ys[]=,i=;i<=n;++i) ys[i]=ys[i-]<<;

    stp=ys[n]<<;

    for (i=;i<=n;++i)

        for (w[i]=read(),x=read();x;x=read()) prt[i]|=ys[x];

    for (i=m-,lg=,rg=;i>=;--i,swap(lg,rg))

        for (j=;j<stp;f[lg][j++]/=n)

            for (f[lg][j]=,k=;k<=n;++k)

                f[lg][j]+=max(((j&prt[k])==prt[k])?f[rg][j|ys[k]]+w[k]:,f[rg][j]);

    printf("%.6lf",f[rg][]);

}

Last Word

　　自己手算一些小数据也是不错的调试技巧。

　　为了缩行可能代码画风会有点崩坏。