ng机器学习视频笔记（二） ——梯度下降算法解释以及求解θ

ng机器学习视频笔记（二）

——梯度下降算法解释以及求解θ

（转载请附上本文链接——linhxx）

 

一、解释梯度算法

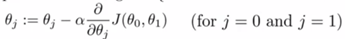
梯度算法公式以及简化的代价函数图，如上图所示。

1）偏导数

由上图可知，在a点，其偏导数小于0，故θ减去小于0的数，相当于加上一个数。另外，从图上可以看出，在a点不是最佳点，需要继续向右移动，即a需要增加。因此符合要求。

对于在b点，可以同理得到需要减少的结果。

2）学习速率α

α表示点移动向最小值点的速率，α取值需要注意。

当值太大，每次移动的距离太长，可能导致在最小值点附近时，移动会超出最小值点的位置，导致不断的在大于、小于最小值点的位置偏移，无法收敛；

当值太小，移动速度 非常慢，会导致程序执行时间太久。

另外，由于在越接近最小值点，偏导数的数量值（绝对值）越小，因此变化速率本身就会变慢，因此选定α后，不需要再去调整数值，其自己会减慢速率。

二、梯度算法缺陷

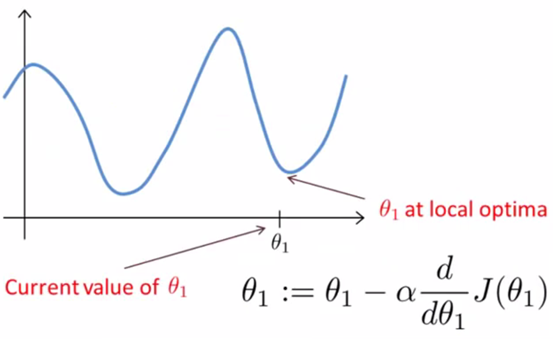
由上图可知，对于有多个极小值点的代价函数，梯度算法只能取到局部最小值点，即函数的极小值点，但是没法保证该点就是最小值点。

三、求解θ

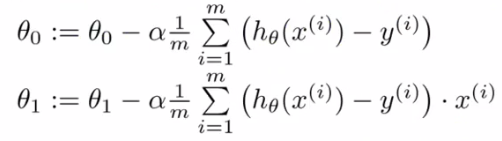
公式如上图所示，实质上就是求偏倒的结果。

不断的计算θ0和θ1，直到偏导数为0（或者设定小于某个阈值），则停止计算，此时的结果则是对于某个起始点的局部最优结果。

——written by linhxx

更多最新文章，欢迎关注微信公众号“决胜机器学习”，或扫描右边二维码。