最近邻查找算法kd-tree

http://blog.csdn.net/pipisorry/article/details/52186307

）选择特征（坐标轴）的方法  （2）以该特征的哪一个为界 （3）达到什么条件算法结束。

(1)选择特征的方法

计算当前观测点集合中每个特征的方差，选择方差最大的一个特征，然后画一个垂直于这个特征的超平面将所有观测点分为两个集合。

（2)以该特征的哪一个值为界 即垂直选择坐标轴的超平面的具体位置。

第一种是以各个点的方差的中值（median）为界。这样会使建好的树非常地平衡，会均匀地分开一个集合。这样做的问题是，如果点的分布非常不好地偏斜的，选择中值会造成连续相同方向的分割，形成细长的超矩形(hyperrectangles)。

替代的方法是计算这些点该坐标轴的平均值，选择距离这个平均值最近的点作为超平面与这个坐标轴的交点。这样这个树不会完美地平衡，但区域会倾向于正方地被划分，连续的分割更有可能在不同方向上发生。

（3）达到什么条件算法结束

实际中，不用指导叶子结点只包含两个点时才结束算法。你可以设定一个预先设定的最小值，当这个最小值达到时结束算法。

      图 6  一个k-d tree划分二维空间

图6中，星号标注的是目标点，我们在k-d tree中找到这个点所处的区域后，依次计算此区域包含的点的距离，找出最近的一个点（黑色点），如果在其他region中还包含更近的点则一定在以这两个点为半径的圆中。假设这个圆如图中所示包含其他区域。先看这个区域兄弟结点对应区域，与圆不重叠；再看其双亲结点的兄弟结点对应区域。从它的子结点对应区域中寻找（图中确实与这个双亲结点的兄弟结点的子结点对应区域重叠了）。在其中找是否有更近的结点。
    k-d tree的优势是可以递增更新。新的观测点可以不断地加入进来。找到新观测点应该在的区域，如果它是空的，就把它添加进去，否则，沿着最长的边分割这个区域来保持接近正方形的性质。这样会破坏树的平衡性，同时让区域不利于找最近邻。我们可以当树的深度到达一定值时重建这棵树。

[【机器学习】K-means聚类算法初探]

分裂结点选择程序

分裂结点的选择通常有多种方法，最常用的是一种方法是：对于所有的样本点，统计它们在每个维上的方差，挑选出方差中的最大值，对应的维就是split域的值。数据方差最大表明沿该维度数据点分散得比较开，这个方向上进行数据分割可以获得最好的分辨率；然后再将所有样本点按其第split维的值进行排序，位于正中间的那个数据点选为分裂结点的dom_elt域。

每次对子空间的划分时，怎样确定在哪个维度上进行划分？

最简单的方法就是轮着来，即如果这次选择了在第i维上进行数据划分，那下一次就在第j(j≠i)维上进行划分，例如：j = (i mod k) + 1。想象一下我们切豆腐时，先是竖着切一刀，切成两半后，再横着来一刀，就得到了很小的方块豆腐。可是“轮着来”的方法是否可以很好地解决问题呢？再次想象一下，我们现在要切的是一根木条，按照“轮着来”的方法先是竖着切一刀，木条一分为二，干净利落，接下来就是再横着切一刀，这个时候就有点考验刀法了，如果木条的直径（横截面）较大，还可以下手，如果直径较小，就没法往下切了。因此，如果K维数据的分布像上面的豆腐一样，“轮着来”的切分方法是可以奏效，但是如果K维度上数据的分布像木条一样，“轮着来”就不好用了。因此，还需要想想其他的切法。

如果一个K维数据集合的分布像木条一样，那就是说明这K维数据在木条较长方向代表的维度上，这些数据的分布散得比较开，数学上来说，就是这些数据在该维度上的方差（invariance）比较大，换句话说，正因为这些数据在该维度上分散的比较开，我们就更容易在这个维度上将它们划分开，因此，这就引出了我们选择维度的另一种方法：最大方差法（max invarince），即每次我们选择维度进行划分时，都选择具有最大方差维度。

在某个维度上进行划分时，怎样确保在这一维度上的划分得到的两个子集合的数量尽量相等，即左子树和右子树中的结点个数尽量相等？

假设当前我们按照最大方差法选择了在维度i上进行K维数据集S的划分，此时我们需要在维度i上将K维数据集合S划分为两个子集合A和B，子集合A中的数据在维度i上的值都小于子集合B中。首先考虑最简单的划分法，即选择第一个数作为比较对象（即划分轴，pivot），S中剩余的其他所有K维数据都跟该pivot在维度i上进行比较，如果小于pivot则划A集合，大于则划入B集合。把A集合和B集合分别看做是左子树和右子树，那么我们在构造一个二叉树的时候，当然是希望它是一棵尽量平衡的树，即左右子树中的结点个数相差不大。而A集合和B集合中数据的个数显然跟pivot值有关，因为它们是跟pivot比较后才被划分到相应的集合中去的。好了，现在的问题就是确定pivot了。给定一个数组，怎样才能得到两个子数组，这两个数组包含的元素个数差不多且其中一个子数组中的元素值都小于另一个子数组呢？方法很简单，找到数组中的中值（即中位数，median），然后将数组中所有元素与中值进行比较，就可以得到上述两个子数组。同样，在维度i上进行划分时，pivot就选择该维度i上所有数据的中值，这样得到的两个子集合数据个数就基本相同了。

kdtree最近邻查找的算法过程

构建好一棵Kd-Tree后，下面给出利用Kd-Tree进行最近邻查找的算法：

（1）将查询数据Q从根结点开始，按照Q与各个结点的比较结果向下访问Kd-Tree，直至达到叶子结点。
其中Q与结点的比较指的是将Q对应于结点中的k维度上的值与m进行比较，若Q(k) < m，则访问左子树，否则访问右子树。达到叶子结点时，计算Q与叶子结点上保存的数据之间的距离，记录下最小距离对应的数据点，记为当前“最近邻点”Pcur和最小距离Dcur。
（2）进行回溯（Backtracking）操作，该操作是为了找到离Q更近的“最近邻点”。即判断未被访问过的分支里是否还有离Q更近的点，它们之间的距离小于Dcur。
如果Q与其父结点下的未被访问过的分支之间的距离小于Dcur，则认为该分支中存在离P更近的数据，进入该结点，进行（1）步骤一样的查找过程，如果找到更近的数据点，则更新为当前的“最近邻点”Pcur，并更新Dcur。如果Q与其父结点下的未被访问过的分支之间的距离大于Dcur，则说明该分支内不存在与Q更近的点。
回溯的判断过程是从下往上进行的，直到回溯到根结点时已经不存在与P更近的分支为止。

怎样判断未被访问过的树分支Branch里是否还有离Q更近的点？

从几何空间上来看，就是判断以Q为中心center和以Dcur为半径Radius的超球面（Hypersphere）与树分支Branch代表的超矩形（Hyperrectangle）之间是否相交。
在实现中，我们可以有两种方式来求Q与树分支Branch之间的距离。第一种是在构造树的过程中，就记录下每个子树中包含的所有数据在该子树对应的维度k上的边界参数[min, max]；第二种是在构造树的过程中，记录下每个子树所在的分割维度k和分割值m，（k, m），Q与子树的距离则为|Q(k) - m|。

kdtree算法实现

构建kd-tree算法的伪代码

1

构建k-d树的伪码

算法：构建k-d树（createKDTree）

输入：数据点集Data-set和其所在的空间Range

输出：Kd，类型为k-d tree

1.If Data-set为空，则返回空的k-d tree

2.调用节点生成程序：

（1）确定split域：对于所有描述子数据（特征矢量），统计它们在每个维上的数据方差。以SURF特征为例，描述子为64维，可计算64个方差。挑选出最大值，对应的维就是split域的值。数据方差大表明沿该坐标轴方向上的数据分散得比较开，在这个方向上进行数据分割有较好的分辨率；

（2）确定Node-data域：数据点集Data-set按其第split域的值排序。位于正中间的那个数据点被选为Node-data。此时新的Data-set' = Data-set\Node-data（除去其中Node-data这一点）。

3.dataleft = {d属于Data-set' && d[split] ≤ Node-data[split]}

Left_Range = {Range && dataleft}
dataright = {d属于Data-set' && d[split] > Node-data[split]}

Right_Range = {Range && dataright}

4.left = 由（dataleft，Left_Range）建立的k-d tree，即递归调用createKDTree（dataleft，Left_Range）。
并设置left的parent域为Kd；

right = 由（dataright，Right_Range）建立的k-d tree，即调用createKDTree（dataright，Right_Range）。
并设置right的parent域为Kd。

2

算法：createKDTree 构建一棵k-d tree
输入：exm_set 样本集
输出 : Kd, 类型为kd-tree
1. 如果exm_set是空的，则返回空的kd-tree
2.调用分裂结点选择程序（输入是exm_set），返回两个值
dom_elt:= exm_set中的一个样本点
split := 分裂维的序号
3.exm_set_left = {exm∈exm_set – dom_elt && exm[split] <= dom_elt[split]}
exm_set_right = {exm∈exm_set – dom_elt && exm[split] > dom_elt[split]}
4.left = createKDTree(exm_set_left)
right = createKDTree(exm_set_right)

k-d tree的最近邻搜索算法

如前所述，在k-d tree树中进行数据的k近邻搜索是特征匹配的重要环节，其目的是检索在k-d tree中与待查询点距离最近的k个数据点。

最近邻搜索是k近邻的特例，也就是1近邻。将1近邻改扩展到k近邻非常容易。下面介绍最简单的k-d tree最近邻搜索算法。

基本的思路很简单：首先通过二叉树搜索（比较待查询节点和分裂节点的分裂维的值，小于等于就进入左子树分支，等于就进入右子树分支直到叶子结点），顺着“搜索路径”很快能找到最近邻的近似点，也就是与待查询点处于同一个子空间的叶子结点；然后再回溯搜索路径，并判断搜索路径上的结点的其他子结点空间中是否可能有距离查询点更近的数据点，如果有可能，则需要跳到其他子结点空间中去搜索（将其他子结点加入到搜索路径）。重复这个过程直到搜索路径为空。下面给出k-d tree最近邻搜索的伪代码：

算法：kdtreeFindNearest /* k-d tree的最近邻搜索 */
输入：Kd /* k-d tree类型*/
target /* 待查询数据点 */
输出 : nearest /* 最近邻数据结点 */
dist /* 最近邻和查询点的距离 */
1. 如果Kd是空的，则设dist为无穷大返回
2. 向下搜索直到叶子结点
pSearch = &Kd
while(pSearch != NULL)  {
pSearch加入到search_path中;
if(target[pSearch->split] <= pSearch->dom_elt[pSearch->split]) /* 如果小于就进入左子树 */
{
pSearch = pSearch->left;
}
else  {
pSearch = pSearch->right;
}
}
取出search_path最后一个赋给nearest
dist = Distance(nearest, target);
3. 回溯搜索路径
while(search_path不为空)  {
取出search_path最后一个结点赋给pBack
if(pBack->left为空 && pBack->right为空) /* 如果pBack为叶子结点 */
{
if( Distance(nearest, target) > Distance(pBack->dom_elt, target) )  {
nearest = pBack->dom_elt;
dist = Distance(pBack->dom_elt, target);
}
}
else {
s = pBack->split;
if( abs(pBack->dom_elt[s] - target[s]) < dist) /* 如果以target为中心的圆（球或超球），半径为dist的圆与分割超平面相交， 那么就要跳到另一边的子空间去搜索 */
{
if( Distance(nearest, target) > Distance(pBack->dom_elt, target) )  {
nearest = pBack->dom_elt;
dist = Distance(pBack->dom_elt, target);
}
if(target[s] <= pBack->dom_elt[s]) /* 如果target位于pBack的左子空间，那么就要跳到右子空间去搜索 */
pSearch = pBack->right;
else
pSearch = pBack->left; /* 如果target位于pBack的右子空间，那么就要跳到左子空间去搜索 */
if(pSearch != NULL)
pSearch加入到search_path中
}
}
}

k-d tree的构建过程及搜索实例

示例1

假设样本集为：{(2,3), (5,4), (9,6), (4,7), (8,1), (7,2)}。构建过程如下：

（1）确定split域，6个数据点在x,y维度上的数据方差分别为39, 28.63。在x轴上方差最大，所以split域值为0（x维的序号为0）

（2）确定分裂节点，根据x维上的值将数据排序，则6个数据点再排序后位于中间的那个数据点为(7,2)，该结点就是分割超平面就是通过(7,2)并垂直于split=0(x)轴的直线x=7

（3）左子空间和右子空间，分割超面x=7将整个空间氛围两部分，x<=7的部分为左子空间，包含3个数据点{(2,3), (5,4), (4,7)}；另一部分为右子空间，包含2个数据点{(9,6), (8,1)}。如下图所示

（4）分别对左子空间中的数据点和右子空间中的数据点重复上面的步骤构建左子树和右子树直到经过划分的子样本集为空。下面的图从左至右从上至下显示了构建这棵二叉树的所有步骤：

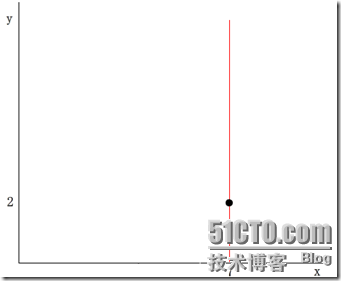
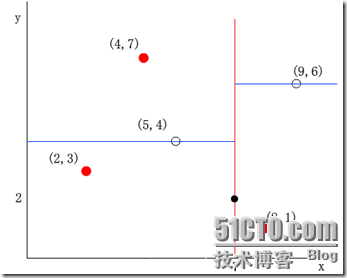
示例2

假设有六个二维数据点 = {（2,3），（5,4），（9,6），（4,7），（8,1），（7,2）}，数据点位于二维空间中。为了能有效的找到最近邻，Kd-树采用分而治之的思想，即将整个空间划分为几个小部分。六个二维数据点生成的Kd-树的图为：

示例3

假设我们的k-d tree就是上面通过样本集{(2,3), (5,4), (9,6), (4,7), (8,1), (7,2)}创建的。将上面的图转化为树形图的样子如下：

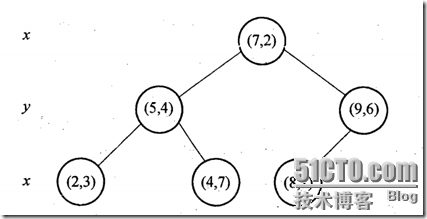
我们来查找点(2.1,3.1)，在(7,2)点测试到达(5,4)，在(5,4)点测试到达(2,3)，然后search_path中的结点为<(7,2), (5,4), (2,3)>，从search_path中取出(2,3)作为当前最佳结点nearest, dist为0.141；

然后回溯至(5,4)，以(2.1,3.1)为圆心，以dist=0.141为半径画一个圆，并不和超平面y=4相交，如下图，所以不必跳到结点(5,4)的右子空间去搜索，因为右子空间中不可能有更近样本点了。

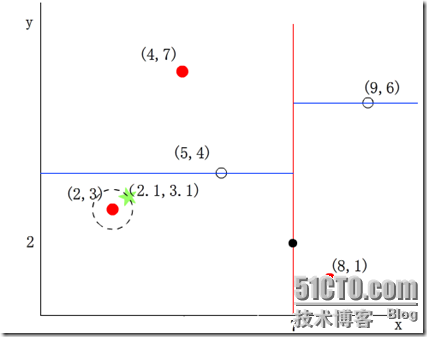
于是在回溯至(7,2)，同理，以(2.1,3.1)为圆心，以dist=0.141为半径画一个圆并不和超平面x=7相交，所以也不用跳到结点(7,2)的右子空间去搜索。

至此，search_path为空，结束整个搜索，返回nearest(2,3)作为(2.1,3.1)的最近邻点，最近距离为0.141。

示例4

再举一个稍微复杂的例子，我们来查找点(2,4.5)，在(7,2)处测试到达(5,4)，在(5,4)处测试到达(4,7)，然后search_path中的结点为<(7,2), (5,4), (4,7)>，从search_path中取出(4,7)作为当前最佳结点nearest, dist为3.202；

然后回溯至(5,4)，以(2,4.5)为圆心，以dist=3.202为半径画一个圆与超平面y=4相交，如下图，所以需要跳到(5,4)的左子空间去搜索。所以要将(2,3)加入到search_path中，现在search_path中的结点为<(7,2), (2, 3)>；另外，(5,4)与(2,4.5)的距离为3.04 < dist = 3.202，所以将(5,4)赋给nearest，并且dist=3.04。

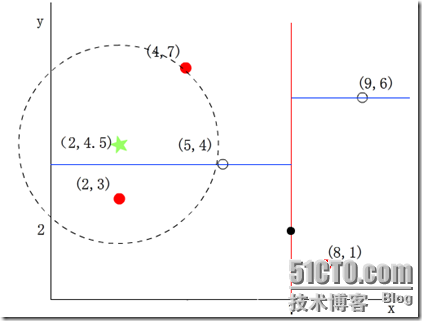
回溯至(2,3)，(2,3)是叶子节点，直接平判断(2,3)是否离(2,4.5)更近，计算得到距离为1.5，所以nearest更新为(2,3)，dist更新为(1.5)

回溯至(7,2)，同理，以(2,4.5)为圆心，以dist=1.5为半径画一个圆并不和超平面x=7相交, 所以不用跳到结点(7,2)的右子空间去搜索。

至此，search_path为空，结束整个搜索，返回nearest(2,3)作为(2,4.5)的最近邻点，最近距离为1.5。

两次搜索的返回的最近邻点虽然是一样的，但是搜索(2, 4.5)的过程要复杂一些，因为(2, 4.5)更接近超平面。研究表明，当查询点的邻域与分割超平面两侧的空间都产生交集时，回溯的次数大大增加。最坏的情况下搜索N个结点的k维kd-tree所花费的时间为：

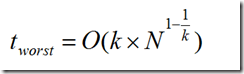
复杂度分析

对于拥有n个已知点的kD-Tree，其复杂度如下：
构建：O(log2n)
插入：O(log n)
删除：O(log n)
查询：O(n1-1/k+m) m---每次要搜索的最近点个数

把最邻近点算法扩展成K-最邻近点算法

...

k-d tree的扩展

Kd-tree with BBF

由于大量回溯会导致kd-tree最近邻搜索的性能大大下降，因此研究人员也提出了改进的k-d tree近邻搜索。

其中一个比较著名的就是 Best-Bin-First，它通过设置优先级队列和运行超时限定来获取近似的最近邻，有效地减少回溯的次数。
Kd-tree在维度较小时（例如：K≤30），算法的查找效率很高，然而当Kd-tree用于对高维数据（例如：K≥100）进行索引和查找时，就面临着维数灾难（curse of dimension）问题，查找效率会随着维度的增加而迅速下降。通常，实际应用中，我们常常处理的数据都具有高维的特点，例如在图像检索和识别中，每张图像通常用一个几百维的向量来表示，每个特征点的局部特征用一个高维向量来表征（例如：128维的SIFT特征）。因此，为了能够让Kd-tree满足对高维数据的索引，Jeffrey S. Beis和David G. Lowe提出了一种改进算法——Kd-tree with BBF（Best Bin First），该算法能够实现近似K近邻的快速搜索，在保证一定查找精度的前提下使得查找速度较快。
在介绍BBF算法前，我们先来看一下原始Kd-tree是为什么在低维空间中有效而到了高维空间后查找效率就会下降。在原始kd-tree的最近邻查找算法中（第一节中介绍的算法），为了能够找到查询点Q在数据集合中的最近邻点，有一个重要的操作步骤：回溯，该步骤是在未被访问过的且与Q的超球面相交的子树分支中查找可能存在的最近邻点。随着维度K的增大，与Q的超球面相交的超矩形（子树分支所在的区域）就会增加，这就意味着需要回溯判断的树分支就会更多，从而算法的查找效率便会下降很大。
一个很自然的思路是：既然kd-tree算法在高维空间中是由于过多的回溯次数导致算法查找效率下降的话，我们就可以限制查找时进行回溯的次数上限，从而避免查找效率下降。这样做有两个问题需要解决：1）最大回溯次数怎么确定？2）怎样保证在最大回溯次数内找到的最近邻比较接近真实最近邻，即查找准确度不能下降太大。

[Kd Tree算法原理和开源实现代码]*

[Kd-tree with BBF]

[k-d tree算法的研究]*

[KD Tree]

[转载：Kd-Tree算法原理和开源实现代码]

[百度百科 kd-tree]

[从K近邻算法、距离度量谈到KD树、SIFT+BBF算法]*

K值的选择

除了上述1.2节如何定义邻居的问题之外，还有一个选择多少个邻居，即K值定义为多大的问题。不要小看了这个K值选择问题，因为它对K近邻算法的结果会产生重大影响。如李航博士的一书「统计学习方法」上所说：

如果选择较小的K值，就相当于用较小的领域中的训练实例进行预测，“学习”近似误差会减小，只有与输入实例较近或相似的训练实例才会对预测结果起作用，与此同时带来的问题是“学习”的估计误差会增大，换句话说，K值的减小就意味着整体模型变得复杂，容易发生过拟合；
如果选择较大的K值，就相当于用较大领域中的训练实例进行预测，其优点是可以减少学习的估计误差，但缺点是学习的近似误差会增大。这时候，与输入实例较远（不相似的）训练实例也会对预测器作用，使预测发生错误，且K值的增大就意味着整体的模型变得简单。
K=N，则完全不足取，因为此时无论输入实例是什么，都只是简单的预测它属于在训练实例中最多的累，模型过于简单，忽略了训练实例中大量有用信息。
    在实际应用中，K值一般取一个比较小的数值，例如采用交叉验证法（简单来说，就是一部分样本做训练集，一部分做测试集）来选择最优的K值。

皮皮blog

k-d tree的实现库

伪代码：

[KD-tree Implement]

python:

[scipy.spatial.KDTree][scipy.spatial]

[KD-tree的原理以及构建与查询操作的python实现]

c/c++:

[kdtree A simple C library for working with KD-Trees]

[http://code.google.com/p/kdtree/]

[https://github.com/sdeming/kdtree]

java:

[KD-Tree Implementation in Java and C#]

from: http://blog.csdn.net/pipisorry/article/details/52186307

ref: [wiki:http://en.wikipedia.org/wiki/K-d_tree]

[Kd Tree算法原理和开源实现代码]*

Paper
[1] Multidimensional binary search trees used for associative searching*
[2] Shape indexing using approximate nearest-neighbour search in high-dimensional spaces
Tutorial
[1] [An intoductory tutorial on kd-trees Andrew W.Moore]
[2] Nearest-Neighbor Methods in Learning and Vision: Theory and Practice