【bzoj2186】: [Sdoi2008]沙拉公主的困惑 数论-欧拉函数

【bzoj2186】: [Sdoi2008]沙拉公主的困惑

考虑当 gcd(a,b)=1 则 gcd(nb+a,b)=1

所以[1,N!]与M!互质的个数就是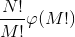

筛出[1,M]所有的素数p[i] 以及逆元 p[i]^-1

处理一下前缀积inv[x]=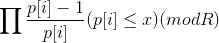

然后答案就是N!*inv[x]

 /* http://www.cnblogs.com/karl07/ */
 #include <cstdlib>
 #include <cstdio>
 #include <cstring>
 #include <cmath>
 #include <algorithm>
 using namespace std;
 #define LL long long
 const int N=1e7;
 int R,T,n,m,cnt=;
 int jc[N+],inv[N+];
 bool pr[N];

 void ex_gcd(int a,int b,int &x,int &y){
     if (b==) {x=;y=;return;}
     ex_gcd(b,a%b,y,x);
     y-=x*(a/b);
 }

 int Inv(int a){
     int x,y;
     ex_gcd(a,R,x,y);
     return (x%R+R)%R;
 }

 void Jc(){
     jc[]=;
     for (int i=;i<=N;i++){
         jc[i]=1ll*jc[i-]*i%R;
     }
 }

 void Prime(){
     inv[]=;
     for (int i=;i<=N;i++){
         inv[i]=inv[i-];
         if (!pr[i]){
             inv[i]=1ll*inv[i]*Inv(i)%R*(i-)%R;
             if (1ll*i*i<=N) for (int j=i*i;j<=N;j+=i){
                 pr[j]=;
             }
         }
     }
 }

 int main(){
     scanf("%d%d",&T,&R);
     Jc();
     Prime();
     for (int i=;i<=T;i++){
         scanf("%d%d",&n,&m);
         printf("%d\n",1ll*jc[n]*inv[m]%R);
     }
     return ;
 }

开long long跑的好慢。。11s卡过去

改成int 快了3s。。

水了一天数论感觉我数论还是这么辣鸡怎么办