计蒜客 17119.Trig Function-切比雪夫多项式+乘法逆元 (2017 ACM-ICPC 亚洲区（西安赛区）网络赛 F)

哈哈哈哈哈哈哈哈哈哈哈哈，终于把这道题补出来了_(:з」∠)_

来写题解啦。

_(:з」∠)_ _(:з」∠)_ _(:з」∠)_ _(:з」∠)_ _(:з」∠)_

哈哈哈哈哈哈，从9月16日打了这个题之后就一直在补这道题，今天终于a了，哈哈哈哈哈哈。

先把代码贴上，有时间再好好写题解，哈哈哈哈哈哈。ヾ(◍°∇°◍)ﾉﾞヾ(◍°∇°◍)ﾉﾞヾ(◍°∇°◍)ﾉﾞヾ(◍°∇°◍)ﾉﾞヾ(◍°∇°◍)ﾉﾞ

代码，嘻嘻:

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 const int N=1e5+;
 const int mod=;
 ll qpow(ll x, int q){
     ll res = ;
     while(q){
     if(q%) res = res*x%mod;
     x = x*x%mod;
     q /= ;
     }
     return res;
 }
 int main(){
     int n,m;
     ll ans;
     while(~scanf("%d%d",&n,&m)){
     if(m>n)printf("0\n");
     else if(n%==&&m%==||n%==&&m%==)printf("0\n");
     else if(n==&&m==)printf("1\n");
     else if(m==){
         if(n%==)printf("0\n");
         else if(n%==){
             if((n/)%==)printf("998244352\n");
             else printf("1\n");
         }
     }
     else{
         ans=;
     for(int i=n-m+;i<=n+m-;i+=)
         ans=(ans*i)%mod;
         ans=(ans*n)%mod;
         ll temp=;
         for(int i=;i<=m;i++)
             temp=(i*temp)%mod;
         ll cnt;
         cnt=qpow(temp,mod-);
         //cout<<"aaaaaaaaaaaaaaaa"<<endl;
         ans=ans*cnt%mod;
         ans=((n-m)/)%==?ans:-ans;
         ans=(ans+mod)%mod;
         printf("%lld\n",ans%mod);
     }
     }
     return ;
 }

溜啦溜啦，哈哈哈哈哈哈哈哈。

今天来写题解啦。

Trig Function

1000ms

131072K

f(cos(x))=cos(n∗x) holds for all x.

Given two integers n and m, you need to calculate the coefficient of x^m in f(x), modulo 998244353.

Input Format

Multiple test cases (no more than 100).

Each test case contains one line consisting of two integers n and m.

1≤n≤10​​⁹,0≤m≤10​⁴​​.

Output Format

Output the answer in a single line for each test case.

样例输入

2 0
2 1
2 2

样例输出

998244352
0
2

题目来源

2017 ACM-ICPC 亚洲区（西安赛区）网络赛

题目一开始没看懂什么意思，后来知道是切比雪夫多项式后，才明白题目要求的是什么。

在多项式中求x^m的系数。

切比雪夫多项式， 自行百度。

切比雪夫多项式的公式:

公式1:

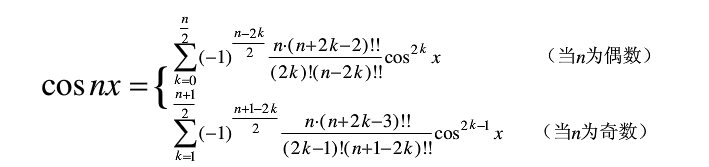
公式2:

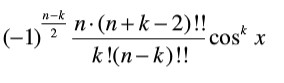
切比雪夫多项式举例:

我是用公式2写的代码。

通过研究这个公式，可以发现:

1.当n和m奇偶性不同的时候，公式结果为0;

2.当m为0的时候可以发现，结果是有规律的。1,0，-1,0,4个一循环，就可以判断if(n%2==1)结果为0，

if((n/2)%2==1),结果为-1，if((n/2)%2==0)结果为1；

3.因为只有n和m同奇或者同偶，用公式计算，通过分析公式2，可以将公式简化。n!!是二阶乘的意思，就是n*(n-2)*(n-4)*(n-6)*...2;

可以将公式上下抵消一部分数，最后可以得到公式的主体部分为n*(n+m-2)*(n+m-2)*...(n-m+2)/m!；

然后就是乘法逆元，将m!逆元，乘法逆元，找度娘。

这个题写的好讨厌，老是小细节出问题，wa了好几好几发_(:з」∠)_

一开始没有将公式优化，也没有用逆元，直接就是超时_(:з」∠)_，改了无数次终于改对了，太菜了，QAQ。

代码解释:

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 const int N=1e5+;
 const int mod=;
 ll qpow(ll x, int q){                      //乘法逆元
     ll res = ;
     while(q){
     if(q%) res = res*x%mod;
     x = x*x%mod;
     q /= ;
     }
     return res;
 }
 int main(){
     int n,m;
     ll ans;
     while(~scanf("%d%d",&n,&m)){
     if(m>n)printf("0\n"); //x的次方数最大为n次，超过了就不存在
     else if(n%==&&m%==||n%==&&m%==)printf("0\n"); //n和m奇偶性不同的时候结果为0
     else if(n==&&m==)printf("1\n");  //如果n和m为0，结果为1
     else if(m==){      //如果m为0，就是有规律的
         if(n%==)printf("0\n");//如果为奇数，就是0
         else if(n%==){  //如果为偶数
             if((n/)%==)printf("998244352\n");//除以2之后如果为奇数就是-1，(-1+mod)%mod结果就是这个数
             else printf("1\n");//除以2之后如果为偶数就是1
         }
     }
     else{  //其他的通过公式进行计算
         ans=;
     for(int i=n-m+;i<=n+m-;i+=) //优化之后只需要进行部分操作就可以
         ans=(ans*i)%mod;//二阶乘
         ans=(ans*n)%mod;//公式
         ll temp=;
         for(int i=;i<=m;i++)
             temp=(i*temp)%mod;//m的阶乘
         ll cnt;
         cnt=qpow(temp,mod-);//m的阶乘的逆元
         //cout<<"aaaaaaaaaaaaaaaa"<<endl;
         ans=ans*cnt%mod;//将结果进行相乘
         ans=((n-m)/)%==?ans:-ans;//判断正负号
         ans=(ans+mod)%mod;
         printf("%lld\n",ans%mod);
     }
     }
     return ;
 }

作为一个数学渣，做这种题目简直要命_(:з」∠)_

这个题也没用到什么很厉害的算法，就是数学题，大佬们肯定很easy的就过了_(:з」∠)_

加油_(:з」∠)_