机器学习：PCA（使用梯度上升法求解数据主成分 Ⅰ ）

一、目标函数的梯度求解公式

• PCA 降维的具体实现，转变为：

　　

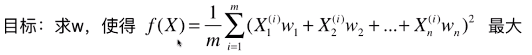
• 方案：梯度上升法优化效用函数，找到其最大值时对应的主成分 w ；

1. 效用函数中，向量 w 是变量；
2. 在最终要求取降维后的数据集时，w 是参数；

　1）推导梯度求解公式

• 变形一

　　　　

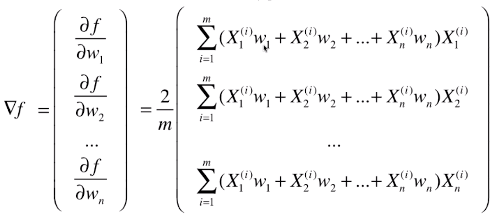
• 变形二

　　　　

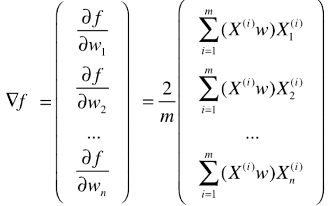
• 变形三：向量化处理

　　　　

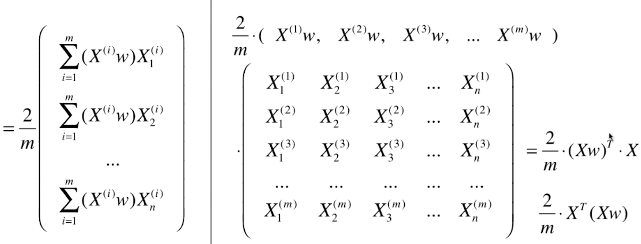
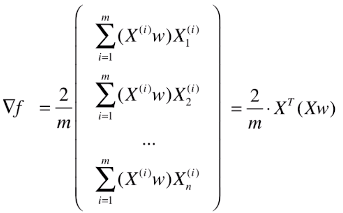
• 最终的梯度求解公式：▽f = 2 / m * X^T . (X . dot(w) )

　　　　

二、代码实现（以二维降一维为例）

• 1）模拟数据

  import numpy as np
  import matplotlib.pyplot as plt
  
  X = np.empty((100, 2))
  X[:, 0] = np.random.uniform(0., 100., size=100)
  X[:, 1] = 0.75 * X[:, 0] + 3. + np.random.normal(0, 10, size=100)

• 2）查看数据分布

  plt.scatter(X[:, 0], X[:, 1])
  plt.show()

• 3）对原始数据集 demean 处理：得到新的数据集，数据集的每一种特征的均值都为 0

  def demean(X):
      return X - np.mean(X, axis=0)
  
  X_demean = demean(X)

1. 数据集的每一个特征，都减去该列特征的均值，使得新的数据集的每一个特征的均值为 0；
2. np.mean(X, axis=0)：得到矩阵 X 每一列的均值，结果为一个列向量；

• 4）使用梯度上升法求解主成分

1. 求当前参数 w 对应的目标函数值（按推导公式求解）

   def f(w, X):
       return np.sum((X.dot(w)**2)) / len(X)

2. 求当前参数 w 对应的梯度值（按推导公式求解）

   def df_math(w, X):
       return X.T.dot(X.dot(w))*2 / len(X)

3. 求当前参数 w 对应的梯度值（按调试公式求解）

   def df_debug(w, X, epsilon=0.0001):
       res = np.empty(len(w))
       for i in range(len(w)):
           w_1 = w.copy()
           w_1[i] += epsilon
           w_2 = w.copy()
           w_2[i] -= epsilon
           res[i] = (f(w_1, X) - f(w_2, X)) / (2 * epsilon)
       return res

4. 将向量 w 转化为单位向量

   def direction(w):
       return w / np.linalg.norm(w)

   # 因为推导公式时人为的将 w 向量的模设为 1，如果不将 w 向量转化为单位向量，梯度上升法的搜索过程会不顺畅；
   # np.linalg.norm(向量)：求向量的模
   # 向量 / 向量的模 == 单位向量

5. 梯度上升法的优化过程

   def gradient_ascent(df, X, initial_w, eta, n_iters=10**4, epsilon=10**-8):
   
       # 将初始化的向量 initial_w 转化为单位向量
       w = direction(initial_w)
       cur_iter = 0
   
       while cur_iter < n_iters:
           gradient = df(w, X)
           last_w = w
           w += eta * gradient
           # 注意1：将每一步优化后的向量 w 也转化为单位向量
           w = direction(w)
           if (abs(f(w, X) - f(last_w, X)) < epsilon):
               break
   
           cur_iter += 1
   
       return w

   # 注意1：每一步优化后的向量 w 都要转化为单位向量

• 5）求解数据的第一主成分

1. 初始化

   initial_w = np.random.random(X.shape[1])
   eta = 0.001

   # 注意2：初始化 w 不能为 0 向量，因为在梯度公式中，若 w 为 0 ，无论什么数据，计算的结果都是没有任何方向的 0；

2. 求解并绘制出第一主成分

   w = gradient_ascent(df_math, X_demean, initial_w, eta)
   
   plt.scatter(X_demean[:,0], X_demean[:,1])
   
   # 此处绘制直线，对应的两个点是（0, 0）、（w[0]*30, w[1]*30）,构成了红色的直线
   # 由于 w[0]、w[1]数值太小，为了让直线看的更清晰，将该点扩大 30 倍
   # 这也是绘制向量的方法
   plt.plot([0, w[0]*30], [0, w[1]*30], color='r')
   plt.show()

   # 注意3：不能用 StandardScaler 标准化数据
   # 原因：由于PCA的过程本身就是求一个轴，使得所有的样本映射到轴上之后方差最大，但是，如果对数据标准化后，则样本的方差就变为 1 了，就不存在方差最大值了；
   # 其实 demean 的过程就是对数据标准化处理的一部分过程，只是没让数据的标准差为 1；
   # 在梯度下降法求解线性回归问题时需要对数据做归一化处理；

　6）求前 n 个主成分

• 求下一个主成分的思路

1. 思路：去掉当前数据集在上一个主成分方向上的分量，得到一个新的数据集，求新的数据集的主成分；
2. 操作：将当前数据集的每一个样本，减去该样本在上一个主成分上的分量
3. 步骤：

   # 1）第一步：求新的数据集
   X2 = np.empty(X.shape)
   for i in range(len(X)):
       X2[i] = X[i] - X[i].dot(w) * w
   # for 循环向量化：X2 = X - X.dot(w).reshape(-1, 1) * w
   # X[i].dot(w)：表示样本 X[i] 在上一主成分 w 方向上的膜
   # X[i].dot(w) * w：表示样本 X[i] 在上一主成分 w 上的分量（为向量）
   # X2[i] = X[i] - X[i].dot(w) * w：表示样本 X[i] 减去其在上一主成分上的分量后的新的样本向量
   
   # 2）第二步：初始化数据，求主成分
   initial_w = np.random.random(X.shape[1])
   eta = 0.01
   w2 = first_component(X2, initial_w, eta)

• import numpy as np
  import matplotlib.pyplot as plt
  
  X = np.empty((100, 2))
  X[:, 0] = np.random.uniform(0, 100, size=100)
  X[:, 1] = 0.75 * X[:,0] + 3. + np.random.normal(0, 10, size=100)
  
  # demean函数，将原始数据集 demean 处理
  def demean(X):
      return X - np.mean(X, axis=0)
  
  # 求当前变量 w 对应的目标函数值
  def f(w, X):
      return np.sum((X.dot(w)**2)) / len(X)
  
  # 求当前变量 w 对应的梯度的值
  def df(w, X):
      return X.T.dot(X.dot(w))*2 / len(X)
  
  # 将向量转化为单位向量
  def direction(w):
      return w / np.linalg.norm(w)
  
  # 求主成分
  def first_component(X, initial_w, eta, n_iters=10**4, epsilon=10**-8):
  
      w = direction(initial_w)
      cur_iter = 0
  
      while cur_iter < n_iters:
          gradient = df(w, X)
          last_w = w
          w += eta * gradient
          w = direction(w)
          if (abs(f(w, X) - f(last_w, X)) < epsilon):
              break
  
          cur_iter += 1
  
      return w
  
  # 求取 X 的前 n 个主成分
  # 求 X 的前 n 个主成分时，只需要对 X 做一次 demean 操作
  def first_n_components(n, X, eta=0.01, n_iters=10**4, epsilon=10**-8):
  
      X_pca = X.copy()
      X_pca = demean(X_pca)
      res = []
      # 循环 n 次，每次求出一个主成分，并将 n 个主成分放在列表 res 中返回
      for i in range(n):
          # 初始化搜索点：initial_w
          initial_w = np.random.random(X_pca.shape[1])
          # 求出主成分 w
          w = first_component(X_pca, initial_w, eta)
          res.append(w)
  
          # 获取下一次主成分的数据集：X_pca，用于计算下一个主成分
          X_pca = X_pca - X_pca.dot(w).reshape(-1,1) * w
  
      return res
  
  # 求数据集 X 的前 2 个主成分
  first_n_components(2, X)
  # 输出：[array([0.7993679 , 0.60084187]), array([-0.60084187,  0.7993679 ])]