平衡树——splay 二

上文传送门：平衡树——splay 一 - yi_fan0305 - 博客园 (cnblogs.com)

OK,我们继续上文，来讲一些其他操作。

七、找排名为k的数

和treap的操作很像，都是通过比较左右子树和该节点的大小来查找。

ll k_th(int x)
{
    int id=root;
    if(siz[id]<x)    return 0;
    while(1)
    {
        int y=ch[id][0];
        if(x>siz[y]+cnt[id])
        {
            x-=(siz[y]+cnt[id]);
            id=ch[id][1];
        }
        else
        {
            if(siz[y]>=x)    id=y;
            else    return val[id];
        }
    }
}

八、清理（一般删除之后用）

void cls(int x)
{
    fa[x]=ch[x][0]=ch[x][1]=siz[x]=cnt[x]=val[x]=0;//清理干净,以绝后患
}

这里要注意，这里只是把该节点的信息删除了，不要忘记把父亲的关系也切断

九、递归建树

相较于单点一个一个插入，在已知点权的情况下，可以直接递归建一棵树，这样效率更高

但是，要注意你是根据数据的下标建的树还是点权建的树，依据不同，操作也不同

其次，为了方便区间操作，一般留出第一个位置（a[1]）和最后一个位置，增加哨兵

a[1]=-INF;
for(rint i=2;i<=n+1;++i)
    a[i]=i-1;
a[n+2]=INF;
root=build(1,n+2,0);

int build(int l,int r,int f)//l 左边界 r 右边界 f 初始化为0
{
    if(l>r)    return 0;
    int mid=l+r>>1;
    fa[mid]=f;
    ch[mid][0]=build(l,mid-1,mid);
    ch[mid][1]=build(mid+1,r,mid);
    pushup(mid);
    return mid;
}

十、下传懒标记

void pushdown(int id)
{
    if(!lazy[id])    return;
    //进行操作......
}

在一些操作中，如旋转、find、翻转、加减，等等，一定不要忘记pushdown

例如：旋转的懒标记下传

void spin(int x)
{
    rint y=fa[x],z=fa[y],d=(x==ch[y][1]);
    pushdown(y),pushdown(x);//懒标记下传
    ch[z][ch[z][1]==y]=x,fa[x]=z;
    ch[y][d]=ch[x][d^1],fa[ch[x][d^1]]=y;
    ch[x][d^1]=y,fa[y]=x;
    pushup(y);
    pushup(x);
}

十一、找数x的排名

这个其实与前面的find一样，只是返回左子树的大小即可

insert(-INF);
insert(INF);
find(x);
printf("%lld\n",siz[ch[root][0]]+(val[root]<x?cnt[root]:0));

void find(ll x)
{
    int u=root;
    if(!u)    return;//不存在该节点,直接返回
    while(ch[u][x>val[u]]&&x!=val[u])//找到该节点的位置
        u=ch[u][x>val[u]];
    splay(u,0);//伸展
}

---

接下来就是区间操作的主场了

区间操作：

区间操作：指定区间（l~r）,查找排序为l-1的节点并伸展至根，查找排序为r+1的节点并伸展至root下，则节点r+1的左子树就是所要的区间。为了操作的方便，在不影响的结果的情况下，可以在两端增加哨兵。

如图依旧扒的教练的

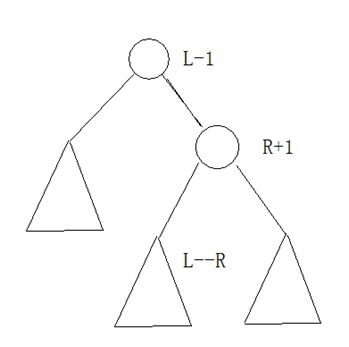
根据二叉查找树的性质，R+1的左孩子就是L--R范围的数据

区间操作都是以这个思路为基础的，前面的删点操作也是运用的这个思路，明白这个，后面才可以进行

pushdown函数随时用上

每次伸展时都要保证懒标记已下传

void check(int now)//保证所有懒标记都下传了
{
    int id=root;
    int k=root;
    while(1)
    {
        pushdown(k);
        if(now==k)break;
        if(now>k)k=ch[k][1];
        else k=ch[k][0];
    }
}

十二、翻转

操作比较简单，交换左右孩子然后下传懒标记即可，但要注意，一棵树被翻转了两次并没有发生变化，所以它的懒标记只有1和0两种，主要注意pushdown函数就好了

建树时要根据下标建树

void pushdown(int id)
{
    if(!rev[id])    return;
    swap(ch[id][0],ch[id][1]);
    rev[ch[id][0]]^=1;
    rev[ch[id][1]]^=1;
    rev[id]=0;
}

void rever(int l,int r)
{
    int pre=find(l-1),nxt=find(r+1);
    splay(pre,0);
    splay(nxt,pre);
    int x=ch[nxt][0];
    rev[x]^=1;
}

十三、区间加、减

和线段树差不多，其实线段树能做的，平衡树也能做到，平衡树能很简单的做到的，线段树就不一定能做到了

在伸展操作之前，一定要保证懒标记都下传了

void pushup(int id)
{
    sum[id]=sum[ch[id][0]]+sum[ch[id][1]]+val[id];
    siz[id]=siz[ch[id][0]]+siz[ch[id][1]]+1;
}

void add(int id,ll v)
{
    if(!id)    return;
    sum[id]+=siz[id]*v;
    laz[id]+=v;
    val[id]+=v;
}

void pushdown(int id)
{
    if(!laz[id])    return;
    add(ch[id][0],laz[id]);
    add(ch[id][1],laz[id]);
    laz[id]=0;
}

void change(int l,int r,int v)
{
    int pre=get(l,0),nxt=get(r,1);
    splay(pre,0);splay(nxt,pre);
    add(ch[nxt][0],v);
    pushup(nxt);
    pushup(pre);
}

十四、区间求和

和线段树操作几乎一模一样

void query(int l,int r)
{
    int pre=get(l,0),nxt=get(r,1);
    splay(pre,0);splay(nxt,pre);
    printf("%lld",sum[ch[nxt][0]]);
}

---

一般用的应该就这些了吧，如果有，我会补充的QWQ！

来自未来的链接：

平衡树——splay 三 - yi_fan0305 - 博客园 (cnblogs.com)