微积分 II 笔记

5.1 定积分的概念

定义

定积分是积分的一种，是函数 $f(x)$ 在区间 $[a,b]$ 上积分和的极限

若 $f(x)$ 在 $[a, b]$ 有界，在 $[a, b]$ 上任意插入 $n$ 个分点将区间分为 $n$ 个小区间 $\Delta x_1, \Delta x_2, ..., \Delta x_n$。在每个小区间上都任取一点 $\xi_i$

记 $\lambda=\max\{\Delta x_1, \Delta x_2, ..., \Delta x_n\}$

那么 $f(x)$ 在 $[a, b]$ 上的定积分 $\int_{a}^{b} f(x)dx=\lim \limits_{\lambda \to 0}\sum_{i=1}^{n} f(\xi_i)\Delta x_i$
定积分只与被积函数与积分区域有关系，与积分变量无关：$\int_{a}^{b}f(x)dx=\int_{a}^{b}f(t)dt$
函数连续即可积；若函数有界，且有有限个间断点，那么也可积
定积分的几何意义

若在 $[a, b]$ 上

$f(x)\geq 0$：函数 $f(x)$ 的图像，直线 $x=a, x=b$ 与 $x$ 轴围成的面积

$f(x)\leq 0$：$...$ 围成的面积的相反数

$f(x)$ 有正有负：$f(x)\geq 0$ 的部分形成的面积减去 $f(x)\leq 0$ 的部分形成的面积
用定义求定积分

求 $\int_{0}^{1} x^2 dx$

将 $[0, 1]$ 等分成 $n$ 份，则 $\Delta x=\frac{1}{n}, \xi_i=\frac{i}{n}$

$\int_{0}^{1}x^2 dx=\lim \limits_{n\to \infty} \sum \Delta x f(\xi_i)=\lim \limits_{n\to \infty} \sum \frac{1}{n}(\frac{i}{n})^2=\lim \limits_{n\to \infty}\frac{1}{n^3}\sum i^2=\lim \limits_{n\to \infty}\frac{n(n+1)(2n+1)}{6n^3}=\frac{1}{3}$

5.2.1 定积分的性质

$\int_{a}^{a}f(x)dx=0$
$\int_{a}^{b}f(x)dx=-\int_{b}^{a}f(x)dx$ (可由性质 $1$ 推出)
$\int_{a}^{b}(\alpha f(x)+\beta g(x))dx=\alpha \int_{a}^{b}f(x)dx+\beta \int_{a}^{b}g(x)dx$
$\int_{a}^{c}f(x)dx=\int_{a}^{b}f(x)dx+\int_{b}^{c}f(x)dx$ (类似向量)

若 $a<b<c$，上式易证 (直接采用几何意义进行理解)

若 $a<c<b$，该式仍然成立：$\int_{a}^{c}f(x)dx=\int_{a}^{b}f(x)dx-\int_{c}^{b}f(x)dx=\int_{a}^{b}f(x)dx+\int_{b}^{c}f(x)dx$ (运用了性质 $2$)
若 $f(x)\geq 0$，则 $\int_{a}^{b}f(x)dx \geq 0$
若 $f(x)\leq g(x)$，则 $\int_{a}^{b}f(x)dx\leq \int_{a}^{b}g(x)dx$
$|\int_{a}^{b}f(x)dx|\leq \int_{a}^{b}|f(x)|dx$
设 $M, m$ 是 $f(x)$ 在 $[a, b]$ 上的最大值与最小值，则有 $m(b-a)\leq \int_{a}^{b}f(x)dx \leq M(b-a)$

即 $\int_{a}^{b} mdx \leq \int_{a}^{b}f(x)dx \leq \int_{a}^{b}Mdx$
定积分中值定理：$f(x)$ 连续，$\exist \xi \in [a, b]$，$\int_{a}^{b}f(x)dx=f(\xi)(b-a)

这一定理由 $8$ 即可推出：由于 $m\leq \frac{\int_{a}^{b}f(x)dx}{b-a}\leq M$，所以一定 $\exist \xi\in [a, b], f(\xi)\in [m, M]$ 使得 $f(\xi)=\frac{\int_{a}^{b}f(x)dx}{b-a}$

5.2.2 微积分基本定理

积分上限函数

$p(x)=\int_{a}^{x} f(t)dt, x\in [a, b]$

积分上限函数的导数 $p'(x)=f(x)$
- 上限是 $x$，直接将 $x$ 代入被积函数：$p(x)=\int_{a}^{x} f(t)dt, p'(x)=f(x)$
- 下限是 $x$，将 $x$ 代入被积函数后加负号：$p(x)=\int_{x}^{a} f(t)d(t)=-\int_{a}^{x} f(t)dt, p'(x)=-f(x)$
- 上限是 $g(x)$：$p(x)=\int_{a}^{g(x)}f(t)dt$，令 $u=g(x)$，则 $p(x)=y=\int_{a}^{u}f(t)dt$，采用复合函数求导链式法则，$p'(x)=\frac{dy}{dx}=\frac{dy}{du} \frac{du}{dx}=f(u)u'=f(g(x))g'(x)$
- 上限是 $g(x)$，下限是 $h(x)$：$p(x)=\int_{h(x)}^{g(x)}f(t)dt=\int_{h(x)}^{a}f(t)dt+\int_{a}^{g(x)}f(t)dt=-\int_{a}^{h(x)}f(t)dt+\int_{a}^{g(x)}f(t)dt=-f(h(x))h'(x)+f(g(x))g'(x)$
积分上限函数的例题
牛顿-莱布尼茨公式 (微积分基本公式)

揭示了定积分与被积函数的原函数或者不定积分之间的联系

$\int_{a}^{b} f(x)dx=F(x)|_{a}^{b}=F(b)-F(a)$

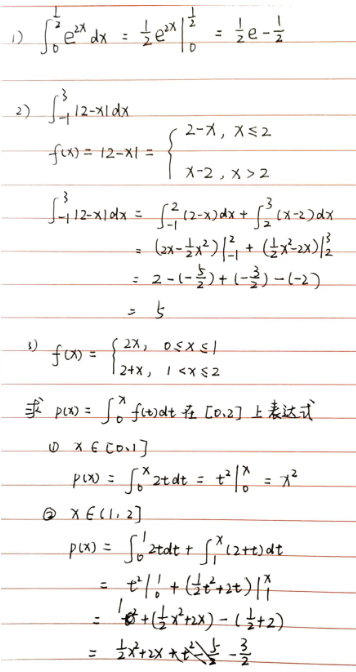
5.3.1 定积分的换元积分法

在使用换元积分法解定积分时
- 新元 $x=\phi(t)$，$\phi(t)$ 必须在被积区间 $[a, b]$ 上单调
- 上下限也变，原变量上(下)限与新变量上(下)限互相对应
奇偶函数被积区间关于原点对称的定积分

$f(x)$ 是偶函数，$\int_{-a}^{a}f(x)dx=2\int_{0}^{a}f(x)dx$

$f(x)$ 是奇函数，$\int_{-a}^{a}f(x)dx=0$

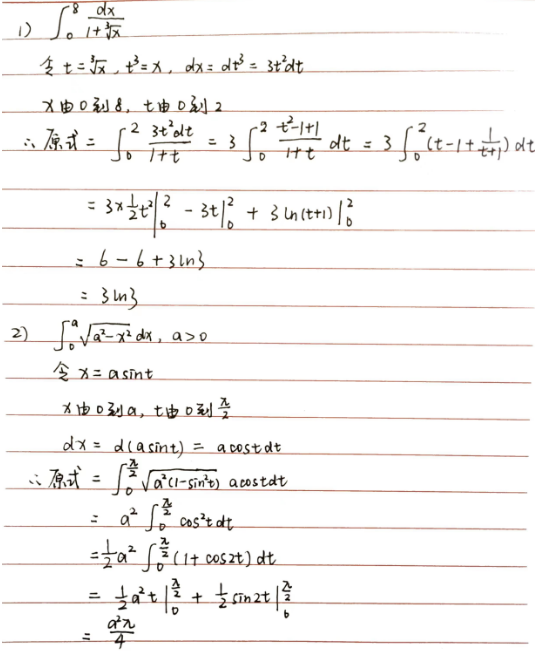
5.3.2 定积分的分部积分法

(定积分的分部积分+上下限)

$\int_{a}^{b} udv=uv|_{a}^{b}-\int_{a}^{b}vdu$

同样遵循反(三角函数)对(数函数)幂(函数，多项式型)三(角函数)指(数函数)的规律决定 $u$ 与 $v$

5.4 定积分的应用

求面积

$\int_{a}^{b}(f(x)-g(x))dx$

想象一把 "量尺"：由 $x$ 轴或 $y$ 轴开始平移 (有时需要将 $f(x),g(x)$ 变换成以 $y$ 为自变量的函数)
求体积

$\int_{a}^{b}A(x)dx$：$A(x)$ 是物体的横截面积

(面积是积点成面，体积是积面成体)
经济问题

5.5.1 广义积分-无穷限积分

广义无穷限积分

$\int_{a}^{+\infty}f(x)dx=\lim \limits_{b\to +\infty} \int_{a}^{b}f(x)dx$

$\int_{-\infty}^{b}f(x)dx=\lim \limits_{a\to -\infty} \int_{a}^{b}f(x)dx$

$\int_{-\infty}^{+\infty}f(x)dx=\int_{-\infty}^{c}f(x)dx+\int_{c}^{+\infty}f(x)dx$
广义牛顿-莱布尼茨定理 (由 $1$ 推出)

$\int_{0}^{+\infty}f(x)dx=F(x)|_{0}^{+\infty}=F(+\infty)-F(0)$

$\int_{-\infty}^{0}f(x)dx=F(x)|_{-\infty}^{0}=F(0)-F(-\infty)$

$\int_{-\infty}^{+\infty}f(x)dx=F(x)|_{-\infty}^{+\infty}=F(+\infty)-F(-\infty)$
性质
- 广义无穷限积分可能是发散的
- 若 $\int_{a}^{+\infty}f(x)dx$ 收敛，则 $\int_{a}^{+\infty}kf(x)dx$ 收敛
- 若 $\int_{a}^{+\infty}f(x)dx$ 与 $\int_{a}^{+\infty}g(x)dx$ 收敛，则 $\int_{a}^{+\infty}(f(x)\pm g(x))dx$ 收敛
- 换元积分法，分部积分法都可以应用在广义无穷限积分上
广义积分的收敛判定
- 法一 (单调有界必收敛)：
  
  若 $f(x)\geq 0$，则 $\int_{a}^{+\infty}f(x)dx$ 收敛 $\iff$ $p(x)=\int_{a}^{x}f(t)dt$ 有界 (注意 $p'(x)=f(x)$)
- 法二 (比较判敛法)：
  
  若 $0\leq f(x) \leq g(x)$：
  
  1）$\int_{a}^{+\infty}g(x)dx$ 收敛，则 $\int_{a}^{+\infty}f(x)dx$ 收敛
  
  2）$\int_{a}^{+\infty}f(x)dx$ 发散，则 $\int_{a}^{+\infty}g(x)dx$ 发散
- 法三 (绝对收敛必收敛)：
  
  $\int_{a}^{+\infty}|f(x)|dx$ 收敛 $\to \int_{a}^{+\infty}f(x)dx$ 收敛
  
  严谨证明：因为有 $0 \leq f(x)-|f(x)| \leq 2|f(x)|$ (分类讨论 $x$ 的符号可证)
  
  应用比较判敛法 $\int_{a}^{+infty} 2|f(x)|dx$ 收敛，则 $\int_{a}^{+infty} (f(x)-|f(x)|)dx$ 收敛
  
  再应用性质 $3$ 推出 $\int_{a}^{+\infty}f(x)dx$ 收敛
应用比较判敛法的一个例题

5.5.2 广义积分-瑕积分

瑕积分

瑕积分是指被积函数带有瑕点的广义积分：瑕点是被积区间中没有定义的点

若在被积区间 $[a, b]$ 中：

$a$ 点无定义：$\int_{a}^{b} f(x)dx=\lim \limits_{\xi^{+} \to 0} \int_{a+\xi^{+}}^{b}f(x)dx$

$b$ 点无定义：$\int_{a}^{b} f(x)dx=\lim \limits_{\xi^{+} \to 0} \int_{a}^{b-\xi^{+}}f(x)dx$

$\exist c \in (a, b)$，$c$ 点无定义，$\int_{a}^{b} f(x)dx=\int_{a}^{c} f(x)dx+\int_{c}^{b}f(x)dx$，转化为上面的两种情况
例题
伽马函数

伽玛函数 (无穷限积分)：$\Gamma (r)=\int_{0}^{\infty}x^{r-1}e^{-x}dx (r>0)$

注意：伽马函数的定义域是 $r>0$，在定义域上连续

伽玛函数的性质：$\Gamma(r+1)=r \Gamma(r) (r>0)$，所以当 $n\in N^{+}$ 时有 $\Gamma(n+1)=n!$

可以看出，伽玛函数是阶乘函数在实数与复数上扩展的一类函数

6.1 空间解析几何

空间直角坐标系(右手系)，空间两点间距离公式

二元函数 $\to$ 曲线，三元函数 $\to$ 曲面

平面方程：$Ax+By+Cz+D=0$，且 $A, B, C$ 不全为 $0$ (如果全为$0$，点集不是平面，而是整个空间)

球面方程：$\sqrt{(x-x_0)^2+(y-y_0)^2+(z-z_0)^2}=R$。若球心是原点，则 $x^2+y^2+z^2=R^2$

柱面：准线(某段曲线)沿着母线平行移动所形成的曲面为柱面。例：$x^2+y^2=0$ (以 $z$ 轴为中心的圆柱面)

旋转抛物面：某段抛物线旋转形成的曲面。例：$x^2+y^2=z$，沿 $z$ 轴方向的切面均为抛物线

鞍面(双曲抛物面)：某段双曲线旋转形成的曲面。例 $y^2-x^2=z$，沿 $z$ 轴方向的切面为抛物线，沿 $x$ 或 $y$ 轴方向的切面为双曲线

6.2 多元函数的基本概念

一些概念在多(三)元函数上的延申

邻域 $U(P_0,\xi)=\{(x, y)|\sqrt{(x-x_0)^2+(y-y_0)^2}<\xi\}$, 去心邻域 $U(P_0,\xi)=\{(x, y)|0<\sqrt{(x-x_0)^2+(y-y_0)^2}<\xi\}$

曲面的内点(一定存在其的一个邻域完全在曲面中)边界点(边界点的邻域全都一部分在曲面内，一部分在曲面外)

曲面是开集(类比开区间，排除边界点)，闭区域(类比闭区间，包括边界点)

曲面的有界(有边界，被围起来)与无界
多元函数的几何意义
多元函数的极限存在条件

回忆一元极限：函数 $f(x)$ 在 $x=x_0$ 处的极限，要求分别从左右两侧向 $x_0$ 逼近的极限相等 $\lim \limits_{x\to x_0^{-}}f(x)=\lim \limits_{x\to x_0^{+}}f(x)(=f(x_0))$

而对于二元函数 $f(x, y)$ 在 $x=x_0, y=y_0$ 处的极限，要求从任意方向 向 $x=x_0, y=y_0$ 逼近的极限都相等；反之在该处极限不存在
求二元函数的极限

方法仍然采用一元函数极限的相关方法：重要极限，等价无穷小，有界 $\times$ 无穷小 $=$ 无穷小

注意：二元函数极限不能使用洛必达法则
二元函数的连续性

回忆一元函数的连续性：函数 $f(x)$ 在 $x_0$ 上连续意味着：

1）函数在 $x=x_0$ 处有定义

2）函数在 $x=x_0$ 处有极限 $\lim \limits_{x\to x_0}f(x)$

3）函数在 $x=x_0$ 处的函数值与极限相等 $\lim \limits_{x\to x_0}f(x)=f(x_0)$

二元函数的连续性定义与一元函数一致：在 $x=x_0, y=y_0$ 处有定义，有极限，定义与极限相等

6.3 偏导数

偏导数

一个多变量的函数的偏导数，就是它关于其中一个变量的导数而保持其他变量恒定

回忆一元函数的导数定义：$\lim \limits_{\Delta x \to 0} \frac{\Delta y}{\Delta x}=\lim \limits_{\Delta x \to 0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$

对于二元函数 $z=f(x, y)$

其对 $x$ 求偏导 ($y$ 不变)：$\lim \limits_{\Delta x \to 0} \frac{\Delta_{x} z}{\Delta x}=\frac{f(x_0+\Delta x, y_0)-f(x_0, y_0)}{\Delta x}$

其对 $y$ 求偏导 ($x$ 不变)：$\lim \limits_{\Delta y\ to 0} \frac{\Delta_{y} z}{\Delta y}=\frac{f(x_0, y_0+\Delta y)-f(x_0, y_0)}{\Delta y}$

关于求偏导的相关题目：对某变量 (例如 $x$) 求偏导，则将其他变量 ($y, z, ...$) 视为常数直接求导即可
偏导数和多元函数连续型

回忆对于一元函数：可导必连续 (见微积分 I - 2.1.2 - 3)

然而对于多元函数：偏导存在不一定连续 (这是因为偏导数只求多元函数在某个方向上的导数，而连续要求多元函数在每个方向上的导数都存在)
偏导数的几何意义

对 $x$ 求偏导：曲面与 $x-z$ 平面相平行的面相截的曲线的导数

对 $y$ 求偏导：曲面与 $y-z$ 平面相平行的面相截的曲线的导数

$...$
二阶偏导数

$\frac{\partial}{\partial x} (\frac{\partial z}{\partial x})=\frac{\partial^2 z}{\partial x^2}=z_{xx}^{''}=f_{xx}^{''}(x, y)$

类似的，还有 $f_{yy}^{''}(x, y)$ 二阶混合偏导数 $f_{xy}^{''}(x, y), f_{yx}^{''}(x, y)$