动态规划 Dynamic Programming 学习笔记

文章以 CC-BY-SA 方式共享，此说明高于本站内其他说明。

本文尚未完工，但内容足够丰富，故提前发布。

内容包含大量 \(\LaTeX\) 公式，渲染可能需要一些时间，请耐心等待渲染（约 5s）。

0x00 前言

题单将介绍介绍动态规划（Dynamic Programming, DP）及其解决的问题、根据其设计的算法及优化。

动态规划是一种通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。

由于动态规划并不是某种具体的算法，而是一种解决特定问题的方法，因此它会出现在各式各样的数据结构中，与之相关的题目种类也更为繁杂。

在 OI 中，计数等非最优化问题的递推解法也常被不规范地称作 DP，因此本章将它们一并列出。事实上，动态规划与其它类型的递推的确有很多相似之处，学习时可以注意它们之间的异同。

0x01 简介

动态规划应用于子问题重叠的情况：

1. 要去刻画最优解的结构特征；
2. 尝试递归地定义最优解的值（就是我们常说的考虑从 \(i - 1\) 转移到 \(i\)）；
3. 计算最优解；
4. 利用计算出的信息构造一个最优解。

0x10 线性 DP

顾名思义，即一般是在数列上/字符串上进行的 DP。

0x11 基本概念

1. 子序列：从一个序列中删去一些数字，剩下的序列称为原序列的子序列。特别的，可以不删。

2. 公共子序列：若 \(c\) 同时为 \(a, b\) 的子序列，则称 \(c\) 为 \(a, b\) 的公共子序列。

3. 最长公共子序列：若 \(c\) 为 \(a, b\) 的公共子序列中长度最大的，则称 \(c\) 为 \(a, b\) 的公共子序列。

0x12 最长上升子序列 LIS 问题

注意，以下的“上升”表示不严格上升，即不下降。

求一个序列 \(a\) 的最长上升子序列，即求一个 \(a\) 的子序列 \(b\) 的长度，其中 \(\forall 1\le i<n, a_i\le a_{i+1}\)。

设 \(f_i\) 表示以 \(a_i\) 为结尾的、最长上升子序列的长度，则很自然的可以想到转移方程：\(f_i=\max(f_{j}+1)\;|\;j<i, a_j\le a_i\)。

这个方程的意思是，在 \(\forall 1\le j<i\) 中寻找一个最大的 \(f_j\)，并满足 \(a_j\le a_i\)。

相当于是把“寻找以 \(a_i\) 为结尾的，最长上升子序列的长度”这个大问题分成了两个小问题：

1. 寻找一个在 \(a_i\) 前面的、比他小的数，并且满足以他为结尾的上升子序列最长。
2. 把 \(a_i\) 接在后边，长度加一。

特别的，\(f_1=1\)。

可以感性理解一下：

\[a=\{1, 2, 5, 3, 4\}\\
f=\{1, 2, 3, 3, 4\}

\]

for (int i = 1; i <= n; ++i)
{
    int p = 0;
    for (int j = 1; j < i; ++j)
        if (a[i] >= a[j])
            p = max(p, f[j] + 1);
    f[i] = p;
}

0x13 扩展：最长上升子序列 LIS 问题 O(n log n) 解法

显然上面的解法是 \(O(n^2)\) 的。但是有更优的、\(O(n \log n)\) 的解法。

设 \(f\) 表示这个最长上升子序列，目前求到的长度为 \(l\)。对于一个元素 \(a_i\)，若 \(a_i\ge f_l\)，则直接将 \(a_i\) 加入到 \(f\) 的末尾。

那如果 \(a_i<f_l\) 呢？这就是保证这个算法正确性的关键了。

给出解决办法：在 \(f\) 数组中找到一个 \(p\)，使得 \(a_i<f_p\) 但 \(a_i\ge f_{p-1}\)，然后用 \(a_i\) 替换掉 \(f_p\)。

分析一下该算法为什么正确。

若 \(p=l\)，那么 \(f_p\) 不如让位给 \(a_i\)，因为由于 \(a_i<f_p\)，显然 \(a_i\) 后面能接的数量比 \(f_p\) 多（比如就恰好有这么一个数 \(x\)，使得 \(a_i\le x<f_p\)，此时若 \(a_i\) 不替换 \(f_p\)，那么 \(x\) 就接不上了，不然 \(x\) 仍然能接上）。

若 \(p\ne l\)，则 \(a_i\) 替换掉 \(f_p\) 完全没问题，因为 \(f_p\) 有生之年不会再被用到了。

这时候就有同学要问了：这样 \(f\) 数组就不保证连续了！

所以 \(f_i\) 其实表示的是：长度为 \(i\) 的最优结尾数字，而不是最长上升子序列。

0x14 最长公共子序列 LCS 问题

给定两个长度为 \(n, m\) 的序列 \(a, b\)，求 \(a, b\) 的最长公共子序列。

设 \(f_{i, j}\) 表示 \(a\) 的前 \(i\) 位与 \(b\) 的前 \(j\) 位所能组成的最长公共子序列。

考虑两种情况：

1. \(a_i=b_j\)，则此时的 \(f_{i,j}=\max(f_{i-1,j},f_{i,f-1},f_{i-1,j-1}+1)\)。
2. \(a_i\ne b_j\)，则 \(f_{i,j}=\max(f_{i-1,j},f_{i,j-1})\)。

对于第一种情况，其实是以下几种情况的最大值：

1. \(a\) 的前 \(i\) 位与 \(b\) 的前 \(j-1\) 位的 LCS 最大值。

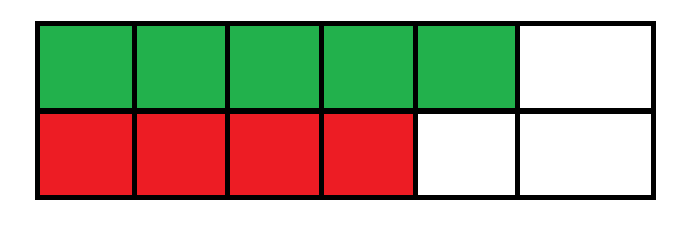
1. \(a\) 的前 \(i-1\) 位与 \(b\) 的前 \(j\) 位的 LCS 最大值。

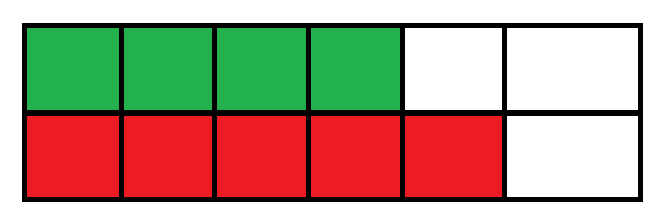
1. \(a\) 的前 \(i-1\) 位与 \(b\) 的前 \(j-1\) 位的 LCS 的最大值，加上当前这一位（也就是选当前这一位）。

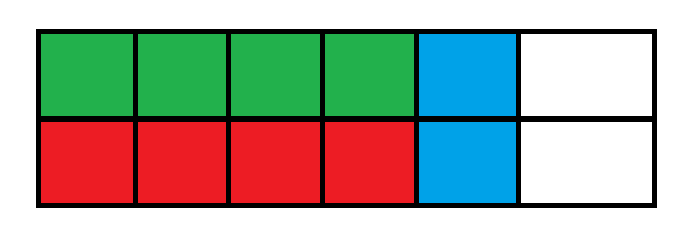
第二种情况同理。

时间复杂度 \(O(nm)\)。

int a[105], b[105], n, m, f[105][105];
int main(void)
{
    cin >> n >> m;
    for (int i = 1; i <= n; ++i)
        cin >> a[i];
    for (int i = 1; i <= m; ++i)
        cin >> b[i];
    for (int i = 1; i <= n; ++i)
    {
        for (int j = 1; j <= m; ++j)
        {
            f[i][j] = max(f[i - 1][j], f[i][j - 1]);
            if (a[i] == b[j])
                f[i][j] = max(f[i][j], f[i - 1][j - 1] + 1);
        }
    }
    printf("%d", f[n][m]);
    return 0;
}

0x15 扩展：最长公共子序列 LCS 问题 O(n log n) 解法

这种解法的本质是将 LCS 转换为 LIS 来求解，求解 LIS 的时间复杂度为 \(O(n\log n)\)，则 LCS 也可以在 \(O(n\log n)\) 的时间复杂度内求出。

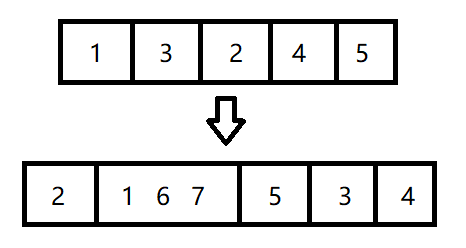
假设 \(a=\{1, 3, 2, 4, 5\}, b=\{3, 1, 4, 5, 2, 3, 3\}\)，记录 \(a\) 中的数在 \(b\) 中出现的位置 \(loc=\{2, \{1, 6, 7\}, 5, 3, 4\}\)。

接下来这一步很关键，将这个 \(loc\) 数组重新映射回 \(a\) 数组中，得到一个新数组 \(c=\{(1)2, (3)1, 6, 7, (2)5, (4)3, (5)4\}\)。求出 \(c\) 数组的 LIS，即为答案。

但这种算法有缺陷：不可以处理有重复元素的序列。

int main()
{
    int i;

    while (scanf("%d", &n) != EOF)
    {
        for (i = 1; i <= n; i++)
            scanf("%d", &a[i]);
        for (i = 1; i <= n; i++)
            scanf("%d", &b[i]);
        calLoc();
        for (i = 1; i <= n; i++)
            b[i] = loc[a[i]];
        printf("%d\n", LIS());
    }
    return 0;
}

0x16 最长公共上升子序列 LCIS 问题

设 \(f_{i, j}\) 表示以 \(a\) 的前 \(i\) 位、\(b\) 的前 \(j\) 位，且以 \(b_j\) 结尾的公共上升子序列的长度。

引理 1：若 \(a_i=b_j\)，则 \(a_i\) 必定与 \(b_j\) 配对。

证明：若 \(b_j\) 不与 \(a_i\) 配对，则 \(b_j\) 必定与 \(a\) 的前 \(i-1\) 项配对（假设 \(f_{i-1, j}>0\)），因为 \(b_j\) 不与 \(a_{i}\) 配对，之后的转移必定没有配对优。

当 \(a_i\ne b_j\) 的时候，由于 \(b_j\) 无法与 \(a_i\) 配对，我们又想让这个公共上升子序列以 \(b_j\) 结尾，那么只能在 \(a\) 序列的前 \(i-1\) 项中找一个数与 \(b_j\) 配对了，所以 \(f_{i, j}=f_{i-1, j}\)。

当 \(a_i=b_j\) 的时候，我们只需要在前面找到一个能将 \(b_j\) 接到后面的最长的公共子序列即可，所以 \(f_{i, j}=\forall 1\le k<j, b_j\ge b_k, \max(f_{i-1, k}+1)\)。

0x17 习题

1. Game Rooms - UVA 12991 - Virtual Judge (vjudge.net)。

   有一个有 \(n\) 层楼的大楼，每一层楼可以建游泳馆 P 或乒乓球房 T，第 \(i\) 层楼有 \(p_i\) 个人打乒乓球，\(t_i\) 个人打羽毛球，请帮忙建造 P 与 T，求每个人到各自游戏室的最小距离之和。

2. #2593. 「NOIP2010」乌龟棋 - 题目 - LibreOJ (loj.ac)。

   有 \(n\) 个格子，\(1\) 为起点，\(n\) 为终点，每个格子上写着一个数字，你的分数就是所有经过的格子的数字之和。你有 \(m\) 张移动卡牌，每张卡牌上标有 \(1, 2, 3, 4\) 中的其中一个数字，使用一张卡牌，就能往前走这张卡牌上写着的数字 格。请求出最多可以获得多少分。

0x20 背包 DP

0x21 0/1 背包

有 \(n\) 个物品和一个容量为 \(v\) 的背包，每个物品有重量 \(w_i\) 和价值 \(v_i\) 两种属性，要求选若干物品放入背包使背包中物品的总价值最大且背包中物品的总重量不超过背包的容量。

0/1 背包，也称单物品背包，是最基础的一类背包 DP 问题。

在上述问题中，每种物品能且仅能被取一次，恰好对应了二进制中的 0/1 两种情况，所以也称 0/1 背包问题。

考虑设 「考虑前 \(i\) 个物品，在背包容量为 \(j\) 的情况下，最大收益」 为 \(f_{i, j}\)。此时让我们考虑下如何转移。每个 \(f_{i, j}\) 只可能有两种情况：选第 \(i\) 种物品、不选第 \(i\) 种物品。

先考虑第一种情况，选第 \(i\) 种物品，那么所获得的收益就是 \(f_{i-1, j-w_i}+v_i\)。即为 「考虑前 \(i-1\) 个物品，背包容量为 \(j-w_i\) 的最大收益」 加上当前物品所能带来的收益 \(v_i\)。

考虑第二种情况，不选第 \(i\) 种物品，显然能获得的最大收益就等于「只考虑前 \(i-1\) 种物品」所获得的最大收益。

综合两种情况，取最大值即为当前的最大收益，所以我们有：

\[f_{i, j} = \max(f_{i-1, j}, f_{i-1, j-w_i}+v_i)

\]

根据 \(f\) 的定义，最后的答案就是 「考虑前 \(n\) 个物品，背包容量为 \(v\) 的最大收益」，也就是 \(f_{n, v}\)。

下面是一个 \(N=4, V=10, w=\{1, 2, 3, 4\}, v=\{1, 4, 6, 8\}\) 的情况：

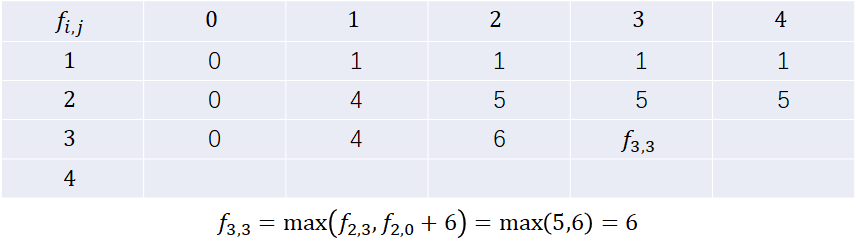
int n, v, f[1005][1005], w[1005], val[1005];

int main(void) {
	cin >> n >> v;
	for (int i = 1; i <= n; ++i) {
		for (int j = 1; j <= v; ++j) {
			if (j < w[i])
				f[i][j] = f[i - 1][j];
			else
				f[i][j] = max(f[i - 1][j], f[i - 1][j - w[i]] + val[i]);//这里的 val[i] 对应题目的 v[i]
		}
	}
}

可这种 DP 显然有一个问题，当 \(n, v \ge 10^4\) 时，程序会 MLE。因为我们使用了一个二维数据来存放 DP 的数据。

有没有什么优化方法？当然有。我们观察代码，发现每一个 f[i][x] 只由 f[i - 1][y] 转移过来，也就是说，\(i\) 逐渐增大的时候， f[i - 2] 及以前的数据我们全部都不需要。

于是我们考虑，只存下 f[i] 与 f[i - 1] ，而不存下以前的数据。这里就需要我们实现滚动数组。

由于 \(i\) 的变化规律一定是 奇数 \(\sim\) 偶数 \(\sim\) 奇数 \(\sim\cdots \sim n\)。那么我们可以使用 · f[i & 1] 来代替 f[i - 1] ， f[!(i & 1)] 来代替 f[i] ，这样保证了使用的交替性。

int n, v, f[2][1005], w[1005], val[1005];

int main(void) {
	cin >> n >> v;
	for (int i = 1; i <= n; ++i) {
		for (int j = 1; j <= v; ++j) {
			if (j < w[i])
				f[!(i & 1)][j] = f[(i & 1)][j];
			else
				f[!(i & 1)][j] = max(f[(i & 1)][j], f[(i & 1)][j - w[i]] + val[i]);//这里的 val[i] 对应题目的 v[i]
		}
	}
	printf("%d", f[n & 1][v]);
	return 0;
}

时间复杂度 \(\Theta (nv)\)，空间复杂度 \(\Theta(v)\)。

但是，我们还是能优化。

为什么我们不能直接省去 \(f\) 的第一维，只留下第二维呢？我们发现，我们实际上更新 \(f_i\) 的时候，只需要用到 \(f_{i-1}\)，而 \(f_{i-1}\) 也只对 \(f_i\) 会产生贡献。所以，我们不妨直接将 \(f_i\) 的数据覆盖到 \(f_{i-1}\) 之前的位置。

于是就有 \(f_j = \max(f_{j-w_i}+v_i, f_j)\)。其中，我们仍需要枚举 \(i\)，只不过二维数组中不需要开原先的第一维。

我们很自然的就会写出下面的代码：

for (int i = 1; i <= n; i++)
  for (int l = w[i]; j <= v; j++)
    f[j] = max(f[j - w[i]] + val[i], f[j]);

哪里错了呢？枚举顺序。

仔细看代码，我们的 \(j\) 是 \(w_i\to v\) 这样子枚举的，而当我们想要去查 \(f_{j - w_i}\) 的时候，查到的其实相当于 \(f_{i, j-w_i}\)，而不是我们想要的 \(f_{i-1, j-w_i}\)。

所以我们可以改变枚举顺序，将 \(j\) 的枚举顺序改为 \(v\to w_i\)。这样，我们查询 \(f_{j-w_i}\) 的时候，由于 \(j-w_i < j\)，我们查到的必定是更新之前的 \(f_{j-w_i}\)。

所以转移方程为

\[f_j=\max(f_j, f_{j-w_i}+v_i)

\]

请务必牢记这个转移方程，在以后的 dp 学习中，我们会经常使用到这种 选、不选 双边决策的问题。

for (int i = 1; i <= n; ++i) {
    for (int j = v; j >= w[i]; --j) {
        f[j] = max(f[j], f[j - w[i]] + val[i]);
    }
}

0x22 完全背包

有 \(n\) 个物品和一个容量为 \(v\) 的背包，每个物品有重量 \(w_i\) 和价值 \(v_i\) 两种属性，要求选若干物品放入背包使背包中物品的总价值最大且背包中物品的总重量不超过背包的容量，每种物品都允许重复选择。

如果你认真思考了为什么 0/1 背包不能顺序（\(j = w_i \sim v\)）的话，你就会很容易的想到——完全背包其实就是顺序枚举的 0/1 背包。

对于我们每次更新的 \(f_j\)，我们会去查找 \(f_{j - w_i}\)，而因为我们是顺序枚举，所以相当于是 \(f_{i, j - w_i}\)。回想一下 \(f\) 数组的定义，\(f_{i, j}\) 表示 「考虑前 \(i\) 个物品，在背包容量为 \(j\) 的情况下，最大收益」。而我们这里查询的是 \(f_{i}\)，不就是相当于重复考虑了第 \(i\) 个物品。

所以代码很显然，就是上面 0/1 背包的“错误”代码。

int main(void) {
	cin >> n >> v;
	for (int i = 1; i <= n; ++i) {
		for (int j = w[i]; j <= v; ++j) {
			f[j] = max(f[j], f[j - w[i]] + val[i]);
		}
	}
	printf("%d", f[v]);
	return 0;
}

0x23 多重背包

有 \(n\) 种物品，一个容量为 \(v\) 的背包，第 \(i\) 种物品有 \(c_i\) 个，重量 \(w_i\)，价值 \(v_i\)。要求选出若干个物品放入背包使得在重量之和不超过背包容量的情况下价值最大。

对于这个问题，有很多种解法，如 \(\Theta(n^3)\)，\(\Theta(n^2 \log n)\)，\(\Theta(n^2)\) 等等，这里只讲前两种做法。

首先考虑最普通的做法，因为第 \(i\) 种物品有 \(c_i\) 个，我们不妨在 0/1 背包的基础上再对每一种物品枚举选的个数 \(k\)。设 \(f_j\) 表示考虑前 \(i\) 种物品，背包容量为 \(j\) 时能获得的最大收益，若第 \(i\) 种选 \(k\) 个，那么所获得的最大收益就是 \(f_j=\max(f_j, f_{j-w_i\times k} + v_i\times k)\)。

考虑优化，第 \(i\) 种物品有 \(c_i\) 个，即相当于有 \(c_i\) 个第 \(i\) 种物品，我们可以直接将第 \(i\) 种物品重复 \(c_i\) 遍，然后跑 0/1 背包，可是这样的时间复杂度和上述方法一样，反而空间复杂度还增加了。

这里我们需要引入一个定理：

对于任意一个正整数 \(x\)，必定可以分解成 \(1,2,4,\cdots,2^{t-1},x-2^{t}+1\,(x-2^{t}+1>0)\) 的形式，且 \(1\sim x\) 中的每一个数均可以被表示成 \(1,2,4,\cdots,2^{t-1},x-2^{t}+1\,(x-2^{t}+1>0)\) 中的数的形式。

那么我们就可以通过这种性质来优化上述代码，对于一个有 \(c_i\) 个的物品 \(i\)，考虑分解成 \(\log c_i\) 个物品的形式。如将一个 \(c_i=13\) 的物品，拆分成 \(4\) 个物品，其 \(v,w\) 如下：

编号	\(v\)	\(w\)
\(1\)	\(v_i\)	\(w_i\)
\(2\)	\(2\times v_i\)	\(2\times w_i\)
\(3\)	\(4\times v_i\)	\(4\times w_i\)
\(4\)	\(6\times v_i\)	\(6\times w_i\)

这样子，无论我们实际选出多少件物品 \(i\)，他总能被分成上述几件物品的组合，如选出 \(11\) 件物品 \(i\)，则相当于选择了上述第 \(1, 3,4\) 物品（\(1+4+6=11\)）。

index = 0;
for (int i = 1; i <= m; i++)
{
    int c = 1, p, h, k;
    cin >> p >> h >> k;
    while (k - c > 0)
    {
        k -= c;
        list[++index].w = c * p;
        list[index].v = c * h;
        c *= 2;
    }
    list[++index].w = p * k;
    list[index].v = h * k;
}

0x24 混合背包

有 \(n\) 种物品，一个容量为 \(v\) 的背包，第 \(i\) 种物品有 \(c_i\) 个，重量 \(w_i\)，价值 \(v_i\)。要求选出若干个物品放入背包使得在重量之和不超过背包容量的情况下价值最大。

特别的，当 \(c_i=-1\) 的情况下，可以无限次选择该物品。

对于这个问题，我们很简单的可以想到，若 \(c_i > 0\)，则可以按照多重背包的方式来解（\(\Theta(n^3)\) 的解法，0/1 背包可以看做是多重背包的一个 \(c_i = 1\) 特殊情况）。当 \(c_i=-1\)，直接按照完全背包的方式来解即可。

0x25 二维代价背包

(LG)P1855 榨取kkksc03

题意简述：有 \(n\) 个愿望，第 \(i\) 个愿望要耗费 \(m_i\) 的金钱与 \(t_i\) 的时间，总共有 \(M\) 元，\(T\) 时间，问最多可以完成多少个愿望。\(1\le n\le 100,1\le m,t\le 200\)。

乍一看题目似乎和 0/1 背包非常相像，都是有 \(n\) 个物品，每个物品都是只能选或不选，而且选会有费用与价值，只不过这里的价值永远为 \(1\)。唯一不同的点在于，这里的费用有两重——金钱与时间。

我们发现不再能通过单一的一个数字来表示出问题的状态了——我们需要考虑两种费用。我们的问题在于，如何将时间、金钱同时表示出来，或者说一个状态如何同时兼顾时间、金钱。

这个问题的答案非常简单，如果一个维度装不下，那么就多加一个维度即可。设 \(f_{j,k}\) 表示当前考虑前 \(i\) 个愿望，在花费 \(j\) 元钱 \(k\) 时间的情况下，最多能满足多少个愿望，显然有以下递推式：

\[f_{j,k}=\max(f_{j,k},f_{j-m_i,k-t_i} + 1)

\]

int main()
{
    cin >> n >> M >> T;
    for(int i = 1; i <= n; ++i) {
        for(int j = M; j >= m[i]; ++j) {
            for(int k = T; k >= t[i]; --k) {
                f[j][k] = max(f[j][k], f[j - m[i]][k - t[i]] + 1);
            }
        }
    }
    cout << f[M][T];
    return 0;
}

0x26 分组背包

(LG)P1757 通天之分组背包

物品被分为了 \(k\) 组，每组最多只能选 \(1\) 个，问最大利用价值。

若物品被分为了 \(k\) 组，只需要考虑每组选哪个物品即可。从 \(1\sim k\) 遍历一下每组，然后再遍历每组中的物品看选择哪一个即可。

形式化的，若设 \(f_{i,j}\) 表示考虑前 \(i\) 组，背包容量为 \(j\) 的情况下的最大收益，那么有：

\[f_{i,j} = \max(f_{i,j}, f_{i-1,j-w_k}+v_k)\;\;(k\in \text{group}_i)

\]

0x27 依赖背包

(LG)P1064 金明的预算方案

如果选第 \(i\) 件物品，就必须选第 \(j\) 件物品，保证不会循环引用，一部分题目甚至会出现多叉树的引用形式。为了方便，就称不依赖于别的物品的物品称为「主件」，依赖于某主件的物品称为「附件」。

这里的依赖关系形成了森林的形状，如样例就是这样一个森林：

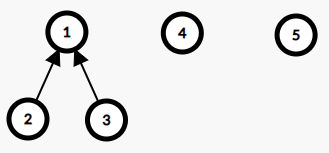
其中 \(a\to b\) 表示 \(a\) 是 \(b\) 的附件。

那么这种情况应该怎么 DP 呢？考虑一下，对于任意一个主件，我们一定会有以下几种处理操作：

1. 不选主件
2. 选主件，不选附件
3. 选择主件 + 附件 1
4. 选择主件 + 附件 2
5. 选择主件 + 附件 1 + 附件 2

而这几种选择又是不能同时成立的，那么直接用上文提到的分组 DP 即可。

#include <iostream>
#define maxn 32005
using namespace std;
int n, m;
int v, p, q;
int main_item_w[maxn];
int main_item_c[maxn];
int annex_item_w[maxn][3];
int annex_item_c[maxn][3];
int f[maxn];
int main()
{
    cin >> n >> m;
    for (int i = 1; i <= m; i++)
    {
        cin >> v >> p >> q;
        if (!q)
        {
            main_item_w[i] = v;
            main_item_c[i] = v * p;
        }
        else
        {
            annex_item_w[q][0]++;
            annex_item_w[q][annex_item_w[q][0]] = v;
            annex_item_c[q][annex_item_w[q][0]] = v * p;
        }
    }

    for (int i = 1; i <= m; i++)
        for (int j = n; main_item_w[i] != 0 && j >= main_item_w[i]; j--)
        {
            f[j] = max(f[j], f[j - main_item_w[i]] + main_item_c[i]);

            if (j >= main_item_w[i] + annex_item_w[i][1])
                f[j] = max(f[j], f[j - main_item_w[i] - annex_item_w[i][1]] + main_item_c[i] + annex_item_c[i][1]);

            if (j >= main_item_w[i] + annex_item_w[i][2])
                f[j] = max(f[j], f[j - main_item_w[i] - annex_item_w[i][2]] + main_item_c[i] + annex_item_c[i][2]);

            if (j >= main_item_w[i] + annex_item_w[i][1] + annex_item_w[i][2])
                f[j] = max(f[j], f[j - main_item_w[i] - annex_item_w[i][1] - annex_item_w[i][2]] + main_item_c[i] + annex_item_c[i][1] + annex_item_c[i][2]);
        }
    cout << f[n] << endl;
    return 0;
}

0x28 习题

1. (LG)P1941 飞扬的小鸟

   提示：混合背包，分类讨论；

2. (LG)P2340 Cow Exhibition G

   提示：背包；转换；

0xFF 参考资料 & 鸣谢

OI Wiki

1. 动态规划部分简介 - OI Wiki (oi-wiki.org)；
2. 动态规划基础 - OI Wiki (oi-wiki.org)；
3. 背包 DP - OI Wiki (oi-wiki.org)；

CSDN

1. 动态规划 —— 线性 DP_Alex_McAvoy的博客-CSDN博客_线性dp；
2. 动态规划 —— 线性 DP —— 序列问题_Alex_McAvoy的博客-CSDN博客；
3. 程序员编程艺术第十一章：最长公共子序列(LCS)问题_v_JULY_v的博客-CSDN博客_lcs 最长公共子序列；
4. 最长上升子序列 (LIS) 详解+例题模板 (全)_lxt_Lucia的博客-CSDN博客_最长上升子序列；
5. nLogn LCS 算法总结_Non_Cease的博客-CSDN博客；
6. 【算法】多重背包问题_AA8j的博客-CSDN博客_多重背包

CN Blog

1. 最长公共子序列（LCS） - ranjiewen - 博客园 (cnblogs.com)；
2. LIS与LCS的nlogn解法 - yzm10 - 博客园 (cnblogs.com)；
3. LCIS 最长公共上升子序列问题DP算法及优化 - ojnQ - 博客园 (cnblogs.com)；
4. 最长公共上升子序列 (LCIS) - _Ackerman - 博客园 (cnblogs.com)；

洛谷博客

1. 题解 P1020 【导弹拦截】 - w1049344862 的博客 - 洛谷博客 (luogu.com.cn)；
2. 题解 P1855 【榨取kkksc03】 - 早右昕 的博客 - 洛谷博客 (luogu.com.cn)；
3. 题解 P1064 【金明的预算方案】 - ShawnZhou 的博客 - 洛谷博客 (luogu.com.cn)；

其他

1. Longest Common Subsequence Simulation (LCS) @jon.andika (sourceforge.net)；
2. tianyicui/pack: 背包问题九讲 (github.com)；