【学习笔记】动态树 Link-Cut Tree

- 闲话

LCT 优秀博客：

$\color{black}{\textsf{F}}\color{red}{\textsf{lashHu}}$ 大佬的 cnblogs：https://www.cnblogs.com/flashhu/p/8324551.html

- 动态树 Link-Cut Tree

- 前置知识

「必学」Splay。
「重要」树链剖分 / 重链剖分（虽然并不需要用到，但是了解重链剖分的思想还是有用的）。
「必学」实链剖分。

实链剖分是一种动态的剖分方式。

对于一个点连向它儿子的所有边，我们选择一条边进行剖分。

被选择的边称为实边，其他边为虚边。

实边连接的儿子称为实儿子。

对于一条实边连接成的链，称为实链。

实链剖分的剖分结果是可变的，可以灵活调整。

和重链剖分的区别就是，重链剖分需要找到儿子子树大小最大的一个连重边，而实链剖分不需要。

- 何为 Link-Cut Tree

给定一棵树，有以下操作：

修改 $x$ 的点权。
求出 $x,y$ 的简单路径的点权和。
修改 $x$ 子树每一点的点权。
求出 $x$ 子树的点权和。

一个很简单的「树链剖分」题目，不是吗？

如果我们增加几个操作呢？

断开 $x \to y$ 这一条边。
连上 $x \to y$ 这一条边。
把这棵树改成以 $x$ 为根。

很显然，因为这棵树要动态删边和加边，且有换根操作，维护静态树的树链剖分就无法处理这类题目了，「动态树 Link-Cut Tree，LCT」应运而生。

具体的，LCT 可以维护以下操作（引自 FlashHu cnblogs）：

查询、修改链上的信息（最值，总和等）
随意指定原树的根（即换根）
动态连边、删边
合并两棵树、分离一棵树
动态维护连通性
更多意想不到的操作

因为 LCT 是动态的数据结构，所以线段树等已不适合维护，引入「Splay」这种平衡树来维护之 $^{\texttt{[1]}}$。

LCT 实质上维护了一个森林，每棵树都由若干棵 Splay 维护。有如下性质：

每棵 Splay 都维护一条原树的路径，这条路径满足节点深度依次增大，且中序遍历 Splay 得到的每个点的深度序列严格递增。单独的一个点也可以是一棵 Splay。
- 举个例子，这棵树的构造为 1(2,3)，即 $1$ 号节点为树根，深度为 $1$，$2,3$ 号节点分别为它的左右儿子，深度为 $2$。那么这个 Splay 森林可以是这样的：
1. $\texttt{[1,2][3]}$，第一棵 Splay 维护 $1 \to 2$ 这条路径，深度单调递增（$1,2$），第二棵维护 $3$，单独的一个点。
2. $\texttt{[1,3][2]}$，第一棵 Splay 维护 $1 \to 3$ 这条路径，深度单调递增（$1,2$），第二棵维护 $2$，单独的一个点。
3. $\texttt{[1][2][3]}$，三个点都为一棵独立的 Splay。
注意 $\texttt{[1,2,3]}$ 这棵 Splay 是不合法的，因为 $2,3$ 的深度相等。
每个节点被包含且仅被包含在一棵Splay 内。
由以上两条性质我们可以得出，每个节点只能和它的儿子连一条实边，其余的儿子都和他连虚边，并且每一条虚边的儿子所在的 Splay 要指向这个节点。但是这个节点并不能指向其儿子的 Splay（即 FlashHu 博客中的认父不认子）。

- 具体操作

- $\text{access}(x)$

LCT 最核心的操作。
打通根节点和指定节点的路径，即把根节点和 $x$ 中间的路径都变成实边，形成一条以根节点开始，指定节点结束的 Splay。

来几张图 $^{\texttt{[2]}}$：

假设一开始实边和虚边是这么划分的：

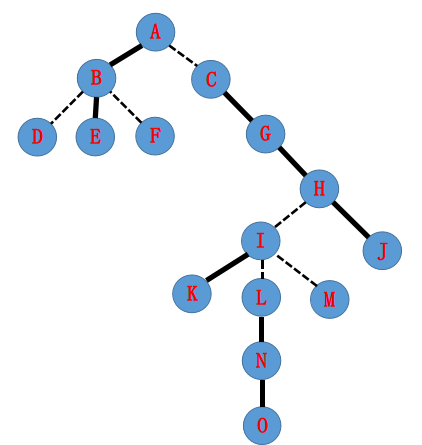
那么所形成的 Splay 森林可能是这样的（绿框中为一个 Splay）：

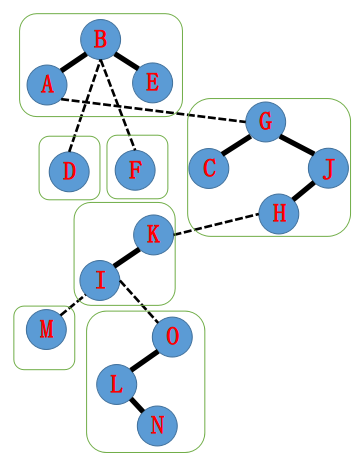
现在我们要 $\text{access(N)}$，把 $\text{A} \to \text{N}$ 的路径都打通成实边，变成一颗 Splay。

根据性质 3，原来有些实边要变虚（因为 $\text{A} \to \text{N}$ 的有些虚边要变实，同层只能有一条实边连向父亲）。那么原树可能要变成这样：

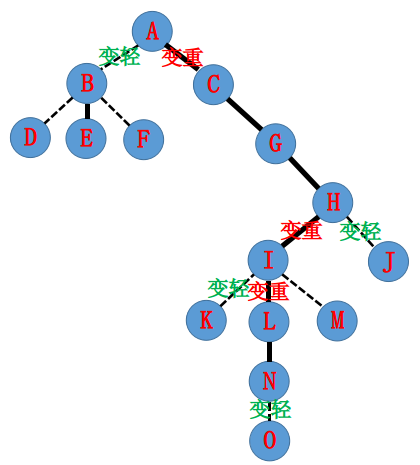
我们一步一步自底向上拉。

首先 $\text{splay(N)}$，把 $\text{N}$ 转到所在 Splay 的根。

因为要 以指定节点结束，所以比他深且在一颗 Splay 中的点要去除。

因为性质 1，中序遍历 Splay 得到的每个点的深度序列严格递增，所以我们把 $\text{N}$ 右边的点去掉即可。即把 $\text{N} \to \text{O}$ 这条边变虚。直接把 $\text{N}$ 的右子树变空，然后让 $\text{O}$ 所在 Splay 指向 $\text{N}$ 即可。

如下图：

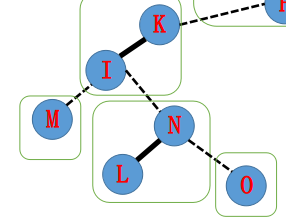
接下来要打通 $\text{I} \to \text{L}$ 的边，首先找到 $\text{N}$ 所在 Splay 指向的节点 $\text{I}$，并 $\text{splay(I)}$，让 $\text{I}$ 转到其所在 Splay 的树根，这样保证它的右儿子肯定是它在原树中连的虚边（性质 1），把它的右子树置空。

然后就可以连接 $\text{I} \to \text{L}$ 了，因为 $\text{L}$ 所指向的点是 $\text{I}$，把 $\text{N}$ 直接连到 $\text{I}$ 的右子树即可。

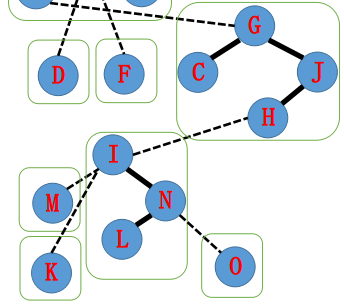
$\text{I}$ 指向 $\text{H}$，接着 $\text{splay(H)}$，把 $\text{H}$ 的右子树直接置为 $\text{I}$ 即可。

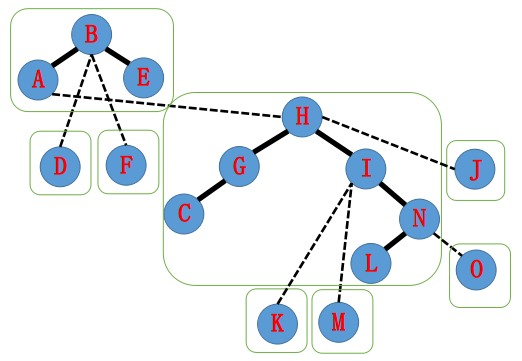
$\text{H}$ 指向 $\text{A}$，于是 $\text{splay(A)}$，把 $\text{A}$ 的右子树更新成 $\text{H}$。

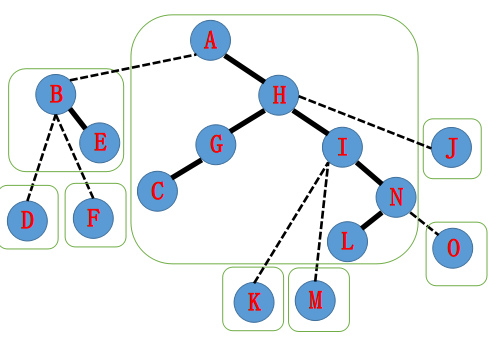
于是 $\text{A} \to \text{N}$ 就在一个 Splay 里了，且正好中序遍历以 $\text{A}$ 开始，以 $\text{N}$ 结束。

代码很简单，只需要四步：

$\text{splay}$ 当前节点，转到根。
找到它所指的父亲，换右儿子。
更新信息，pushup。
把当前节点变成它的轻边所指的父亲，转 $1$。

inline void access(int x){

	for(int y=0;x;y=x,x=fa[x])

		splay(x),ch[x][1]=y,pushup(x);

}

- $\text{makeroot}(x)$

把 $x$ 拉到整棵树的根。

在介绍 $\text{makeroot}$ 前，先来回顾一下 Splay 的区间反转操作，不熟悉的可以看一下模板题。

- $\text{pushr(x)}$

我们注意到，将 $[l,r]$ 这一段区间反转，相当于对于 $l \le id \le r$ 的每一个节点的左右子树自上而下 反转。

引用几张图 $^{\texttt{[3]}}$：

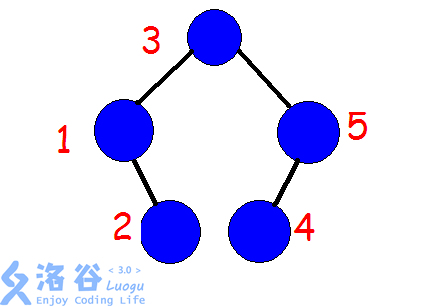
这是一棵树，那么如果我们想翻转 $[2,4]$ 这个区间，只需要 $\text{splay}$ $1$ 和 $5$，使得 $5$ 的左子树都是 $>1$ 且 $<5$ 的（二叉平衡树的性质），于是只需要反转 $[2,4]$ 的左右子树了。

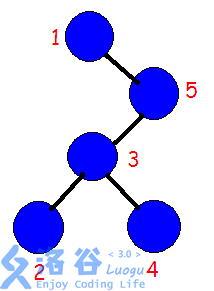
但在这个地方我们可以考虑打个标记，标记的存在就只在于记录现在对于当前节点应不应该翻转两个子树。

接下来回到 $\text{makeroot}$。

首先显然要把根节点到 $x$ 的路径打通，否则根节点和 $x$ 都不在一棵 Splay 中，谈何换根。

所以我们先 $\text{access}(x)$，然后根节点到 $x$ 就是一条实路径，且中序遍历以根节点开头，以 $x$ 结尾。不难发现此时 $x$ 就是这颗 Splay 中深度最深的点。然后我们先 $\text{splay}(x)$，使得 $x$ 节点为这颗 Splay 的根，（注意不是整棵树的根，因为先序遍历仍以原先根节点开始）。这时候 $x$ 没有右子树。因为 $x$ 的深度最深，这时候我们翻转一下，$\text{pushr}$，把这一棵 Splay 深度都改变，这时候 $x$ 就变成的这棵树最上面的节点（真正的根，它没有左子树），大功告成。

inline void pushr(int x){

	swap(lc(x),rc(x));

	r[x]^=1;

}

inline void makeroot(int x){

	access(x); splay(x);

	pushr(x);

}

- $\text{findroot}(x)$

找到 $x$ 所在原树的根，主要用来判断两点的连通性（即如果 $\text{findroot}(x)=\text{findroot}(y)$ 表明 $x,y$ 在一棵树中）。

我们先把根节点到 $x$ 的路径打通，然后 $\text{splay}(x)$，把 $x$ 转到这棵 Splay 的根（不是原树的根，没有破坏结构），这时候根据二叉排序树的性质，所有深度比 $x$ 小的点都在 $x$ 的左子树，循环找下去，直到叶节点即可。

注意往下找左儿子的时候，一定要下放翻转标记，不然可能会导致 Splay 信息不正确。

inline int findroot(int x){

	access(x); splay(x);

	while(lc(x)) pushdown(x),x=lc(x); // 一定要 pushdown！

	splay(x); // 保证复杂度

	return x;

}

- $\text{split}(x,y)$

指定出一条 $x \to y$ 路径的 Splay。

先 $\text{makeroot}(x)$，把 $x$ 变成当前树的根，然后 $\text{access}(y)$，提取 $x \to y$ 的路径。最后 $\text{splay}(y)$ 保证复杂度。这样访问这个 Splay 的时候只需要访问 $y$ 就可以了。

inline void split(int x,int y){

	makeroot(x); access(y);

	splay(y);

}

- $\text{nroot}(x)$

判断当前节点是否是它所在 Splay 的根。

原理很简单，如果他是 Splay 的根（即它和它的父亲连的是虚边），它的父亲的儿子里没有它（它的父亲连到它的实儿子了）。

如果返回 true，就说明它不是根。

inline bool nroot(int x){

	return lc(fa[x])==x || rc(fa[x])==x;

}

- $\text{link}(x,y)$

连上 $x \to y$ 的边。

可以自行决定把 $x$ 的父亲设为 $y$ 还是把 $y$ 的父亲设为 $x$，这里我把 $x$ 的父亲设为 $y$，即在 $x,y$ 间连一条轻边。

代码也很简单，如下：

inline bool link(int x,int y){

	makeroot(x); // 使 x 成为它所在的树的根

	if(findroot(y)==x) return 0;  // 两点已在一棵树内，连边不合法

	fa[x]=y;

	return 1;

}

如果题目保证连边合法，代码就可以更简单：

inline void link(int x,int y){

	makeroot(x);

	fa[x]=y;

}

- $\text{cut}(x,y)$

断开 $x \to y$ 的边。

如果题目保证合法，这个操作倒是很容易。

先提取出 $x \to y$ 的路径（即 $\text{split}(x,y)$），然后因为 $y$ 变成了 Splay 的根（见 $\text{split}$ 那一段，最后有说明），$x$ 必在它的左子树上

（关于左子树有必要做个说明：因为我们是先 $\text{makeroot}(x)$，然后 $\text{access}(y)$ 的，所以$x$ 在 Splay 中深度一定比 $y$ 浅，于是当 $\text{splay}(y)$ 之后，$x$ 必在它的左子树）。

于是代码就有了：

inline bool cut(int x,int y){

	split(x,y);

	fa[x]=lc(y)=0;

	pushup(y); // y少了个儿子

}

但是如果没有保证连边合法呢？

我们先要看 $x,y$ 是否在一棵 Splay 中（否则原来就断开的，不合法）。
然后我们要看 $x,y$ 有无父子关系，不然不合法。
最后我们要看中序遍历下，$x,y$ 中间有无其他节点（即 $y$ 有没有右子树）。

三个关系都满足就可以了。

这里注意 $\text{findroot}(y)$ 之后 $x$ 是原树的树根，而且因为 $\text{findroot}$ 里先 $\text{access}(y)$ 的，所以 $y$ 一定在 $x$ 的右子树。

inline bool cut(int x,int y){

	makeroot(x);

	if(findroot(y)!=x || fa[y]!=x || lc(y)) return 0;

	fa[y]=rc(x)=0;

	pushup(x);

	return 1;

}

至此，LCT 的基本操作就讲完啦！

LCT 中不同于普通 Splay 的几个点

$\text{splay}$ 时，一定要先判断要转的点是不是根！
- 否则你会发现 fa[x]=0 且 fa[fa[x]]=0，然后你的 Splay 就寄了。
$\text{splay}$ 前要先堆栈下放标记。
- 否则你会发现你的 Splay 标记乱成一团，又寄了 $\texttt{:(}$。

完整代码

模板题：https://www.luogu.com.cn/problem/P3690。

维护其他什么操作的话改一下 pushup 即可。

#include <bits/stdc++.h>

using namespace std;

inline char gc(){

    static char buf[100000],*p1=buf,*p2=buf;

    return p1==p2&&(p2=(p1=buf)+fread(buf,1,100000,stdin),p1==p2)?EOF:*p1++;

}

inline int read(){

    char ch=gc(); int x=0; bool f=0;

    while(!(ch>='0'&&ch<='9'))f|=(ch=='-'),ch=gc();

    while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=gc();

    return f?-x:x;

}

const int N = 2e5+5;

class _lct{

#define lc(x) ch[x][0]

#define rc(x) ch[x][1]

public:

	int ch[N][2],val[N],fa[N],s[N],stk[N];

	bool r[N];

	inline bool nroot(int x){

		return lc(fa[x])==x || rc(fa[x])==x;

	}

	inline void pushr(int x){

		swap(lc(x),rc(x));

		r[x]^=1;

	}

	inline void pushup(int x){

		s[x]=s[lc(x)]^s[rc(x)]^val[x];

	}

	inline void pushdown(int x){

		if(r[x]){

			if(lc(x)) pushr(lc(x));

			if(rc(x)) pushr(rc(x));

			r[x]=0;

		}

	}

	inline void rotate(int x){

		int y=fa[x],z=fa[y];

		int k=rc(y)==x,w=ch[x][!k];

		if(nroot(y)) ch[z][rc(z)==y]=x; ch[x][!k]=y; ch[y][k]=w;

		if(w) fa[w]=y; fa[x]=z,fa[y]=x;

		pushup(y);

	}

	inline void splay(int x){

		int y=x,z=0;

		stk[++z]=y;

		while(nroot(y)) stk[++z]=y=fa[y];

		while(z) pushdown(stk[z--]);

		while(nroot(x)){

			y=fa[x]; z=fa[y];

			if(nroot(y)) rotate((lc(z)==y)^(lc(y)==x)?x:y);

			rotate(x);

		}

		pushup(x);

	}

	inline void access(int x){

		for(int y=0;x;x=fa[y=x])

			splay(x),rc(x)=y,pushup(x);

	}

	inline void makeroot(int x){

		access(x); splay(x);

		pushr(x);

	}

	inline int findroot(int x){

		access(x); splay(x);

		while(lc(x)) pushdown(x),x=lc(x);

		splay(x);

		return x;

	}

	inline void split(int x,int y){

		makeroot(x); access(y);

		splay(y);

	}

	inline bool link(int x,int y){

		makeroot(x);

		if(findroot(y)==x) return 0;

		fa[x]=y;

		return 1;

	}

	inline bool cut(int x,int y){

		makeroot(x);

		if(findroot(y)!=x || fa[y]!=x || lc(y)) return 0;

		fa[y]=rc(x)=0;

		pushup(x);

		return 1;

	}

}lct;

int n,m;

int main(){

	n=read(); m=read();

	for(int i=1;i<=n;i++) lct.val[i]=read();

	while(m--){

		int opt,x,y;

		opt=read(); x=read(); y=read();

		switch(opt){

			case 0:{lct.split(x,y); printf("%d\n",lct.s[y]); break;}

			case 1:{lct.link(x,y); break;}

			case 2:{lct.cut(x,y); break;}

			case 3:{lct.splay(x); lct.val[x]=y; break;}

		}

	}

	return 0;

}

- Reference

$\texttt{[1]}$：因为 LCT 的 makeroot 等操作需要翻转一棵树，使得 Treap 等平衡树均已不适用，但是 FHQ Treap 或许也可以维护，详见 https://immortalco.blog.uoj.ac/blog/2342。

$\texttt{[2]}$：引自 https://www.cnblogs.com/flashhu/p/8324551.html

$\texttt{[3]}$：引自 https://www.luogu.com.cn/blog/pks-LOVING/splay-chu-li-ou-jian-cao-zuo-fan-zhuai-cao-zuo-reverse