kruskal 及其应用

kruskal

最小生成树

kruskal 是一种常见且好理解的最小生成树（MST）算法。

前置知识

• 并查集和路径压缩

生成树

在有 n 的顶点的无向图中，取其中 n-1 条边相连，所得到的树即为生成树。

最小生成树就是生成树边权和最小。

kruskal 求 MST

kruskal 基于贪心。

如果让你的选择之和最小，该怎么选？

每次选择的边权都是没选过的最小的，直到选了 n-1 条边。

但这样选有时会出问题。

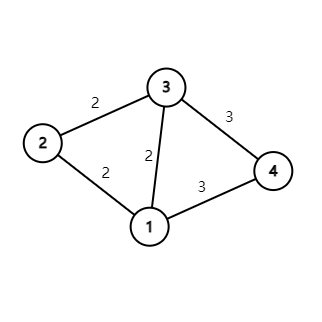
如上图，选最小的边应该是：

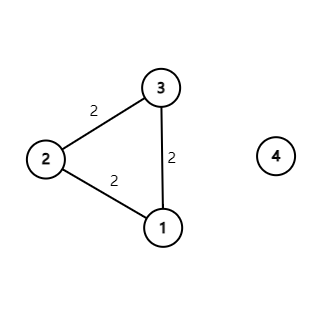
但显然，这不是一个树。

所以在连边之前，还要判断一下两个点是否在同一个连通块内。

判联通用什么？

对，并查集！

那么整个 kruskal 的过程就是：

排序，判联通，加边。

Code(P3366)

#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std;
int re()
{
	int s=0,f=1;char ch=getchar();
	while(ch>'9'||ch<'0')
	{
		if(ch=='-')f=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9')
		s=s*10+ch-48,ch=getchar();
	return s*f;
}
void wr(int s)
{
	if(s<0)putchar('-'),s=-s;
	if(s>9)wr(s/10);
	putchar(s%10+48);
}
const int inf=1e5+7;
int n,m,cnt,ans;
struct kruskal{
	int from,to,val;
	bool operator <(const kruskal &b)const
	{
		return val<b.val;
	}
};
vector<kruskal>h;
int fa[inf];
int find(int x)
{
	if(x==fa[x])return fa[x];
	return fa[x]=find(fa[x]);
}
int main()
{
	n=re();m=re();
	for(int i=1;i<=n;i++)fa[i]=i;
	for(int i=1;i<=m;i++)
	{
		int u=re(),v=re(),w=re();
		h.push_back((kruskal){u,v,w});
	}
	sort(h.begin(),h.end());
	int len=h.size();
	for(int i=0;i<len;i++)
	{
		int r1=find(h[i].from),r2=find(h[i].to);
		if(r1==r2)continue;
		cnt++;ans+=h[i].val;
		fa[r1]=r2;
		if(cnt==n-1)break;
	}
	wr(ans);
    return 0;
}

练习

P4826

P2212

次小生成树

前置知识：

• 倍增在树上的应用

为方便叙述，最小生成树中的 \(n-1\) 边叫做树边，剩余的 \(m-n+1\) 条边叫非树边。

非严格次小生成树

显然，对于已经生成的最小生成树来说，每一条非树边的加入，都会形成一个环。那么再将环上的树边中最大的边删除，就能得到次小生成树的一颗候选树。

令最小生成树大小为 \(minn\)，新加入的非树边权值为 \(new\)，环上的最大树边为 \(max\)，那么候选树的大小就是 \(minn-max+new\)，我们所求则是 \(min\{minn-max+new\}\)。

严格次小生成树

当 \(new=max\) 时，若按上述方法进行维护，得到的 \((minn-max+new)=minn\)。

此时，就应该选择环上树边的次大值 \(nexm\)，\((minn-nexm+new)>minn\)。

解法

现在的问题就在于，如何快速求出两点间树边的最大值和次大值。

若直接用两个二维数组将两点间的最大值，次大值存下来是不现实的，\(O(n^2)\) 的空间复杂度不允许。

考虑倍增，储存下来每个节点到其 \(2^k\) 级祖先的最大值和次大值，然后在跳 lca 的过程中维护最大值和次大值。

比如，求从 u 到 v 的最大值，可以先找出 u 和 v 的 lca，然后分别求出 u 到 lca 和 v 到 lca 的最大值，两者取最大即可。

Code:

#include<cstdio>
#include<algorithm>
#include<vector>
#define int long long
using namespace std;
int re()
{
	int s=0,f=1;char ch=getchar();
	while(ch>'9'||ch<'0')
	{
		if(ch=='-')f=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9')
		s=s*10+ch-48,ch=getchar();
	return s*f;
}
void wr(int s)
{
	if(s<0)putchar('-'),s=-s;
	if(s>9)wr(s/10);
	putchar(s%10+48);
}
const int inf=3e5+7;
int n,m,minn,ans=1e18;
int fa[inf];
struct kruskal{
	int from,to,val;
	bool operator <(const kruskal &b)const
	{
		return val<b.val;
	}
};
vector<kruskal>k;
struct edge{
	int to,val;
	edge(int to,int val):
		to(to),val(val){}
};
vector<edge>e[inf];
bool vis[inf<<1];int cnt;
int find(int s)
{
	if(s==fa[s])return s;
	return fa[s]=find(fa[s]);
}
int dep[inf],fat[inf][20];
int maxn[inf][20],nexm[inf][20];
void dfs(int now,int from)
{
	dep[now]=dep[from]+1;
	fat[now][0]=from;
	for(int i=0;i<e[now].size();i++)
	{
		int p=e[now][i].to;
		if(p==from)continue;
		maxn[p][0]=e[now][i].val;
		dfs(p,now);
	}
}
void swap(int &a,int &b){a^=b^=a^=b;}
int max(int a,int b){return a>b?a:b;}
int _lca(int x,int y)
{
	if(dep[x]<dep[y])swap(x,y);
	for(int i=19;i>=0;i--)
		if(dep[fat[x][i]]>=dep[y])
			x=fat[x][i];
	if(x==y)return x;
	for(int i=19;i>=0;i--)
		if(fat[x][i]!=fat[y][i])
			x=fat[x][i],y=fat[y][i];
	return fat[x][0];
}
int ask(int x,int y,int z)
{
	int maxi=0;
	for(int i=19;i>=0;i--)
	{
		if(dep[fat[x][i]]>=dep[y])
		{
			if(maxn[x][i]==z)
				maxi=max(maxi,nexm[x][i]);
			else maxi=max(maxi,maxn[x][i]);
			x=fat[x][i];
		}
	}
	return maxi;
}
signed main()
{
	n=re();m=re();ans+=7;
	for(int i=1;i<=n;i++)fa[i]=i;
	for(int i=1;i<=m;i++)
	{
		kruskal data;
		data.from=re(),data.to=re(),data.val=re();
		k.push_back(data);
	}
	sort(k.begin(),k.end());
	for(int i=0;i<m;i++)
	{
		int k1=k[i].from,k2=k[i].to,v=k[i].val;
		int r1=find(k1),r2=find(k2);
		if(r1==r2)continue;
		vis[i]=1;fa[r1]=r2;
		cnt++;minn+=v;
		e[k1].push_back(edge(k2,v));
		e[k2].push_back(edge(k1,v));
		if(cnt==n-1)break;
	}
	dfs(1,1);
	for(int i=1;i<20;i++)
	{
		for(int j=1;j<=n;j++)
		{
			fat[j][i]=fat[fat[j][i-1]][i-1];
			maxn[j][i]=max(maxn[j][i-1],maxn[fat[j][i-1]][i-1]);
			if(maxn[j][i-1]==maxn[fat[j][i-1]][i-1])
				nexm[j][i]=max(nexm[j][i-1],nexm[fat[j][i-1]][i-1]);
			else if(maxn[j][i-1]<maxn[fat[j][i-1]][i-1])
				nexm[j][i]=max(maxn[j][i-1],nexm[fat[j][i-1]][i-1]);
			else if(maxn[j][i-1]>maxn[fat[j][i-1]][i-1])
				nexm[j][i]=max(nexm[j][i-1],maxn[fat[j][i-1]][i-1]);
		}
	}
	for(int i=0;i<m;i++)
	{
		if(vis[i])continue;
		int k1=k[i].from,k2=k[i].to,val=k[i].val;
		int lca=_lca(k1,k2);
		int max1=ask(k1,lca,val),max2=ask(k2,lca,val);
		ans=min(ans,minn+val-max(max1,max2));
	}
	wr(ans);putchar('\n');
	return 0;
}

kruskal 重构树

用途

巧妙地求解询问连接两点的所有路径中最大边的最小值或者最小边的最大值问题。

思路

kruskal 求 MST 的时候是逐步加边，而 kruskal 重构树则是将要加的边转化成点，并连接原来的两个点，边权为点权。

就像这样：

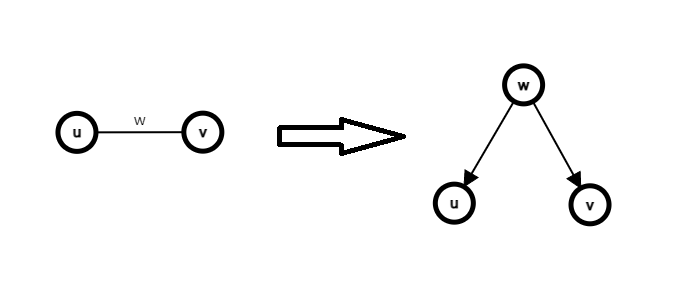
实例（图片来自 OI-Wiki）

原无向图

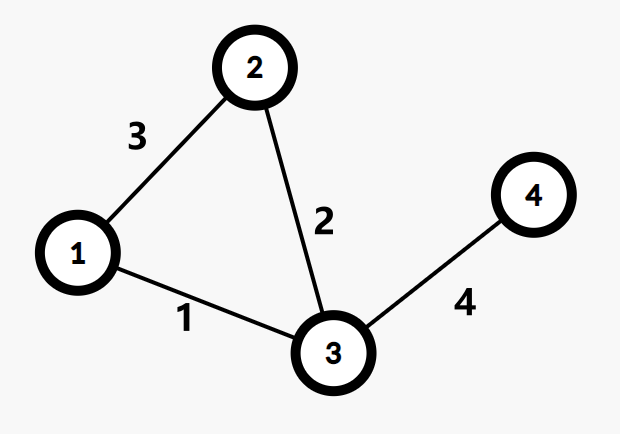
重构树

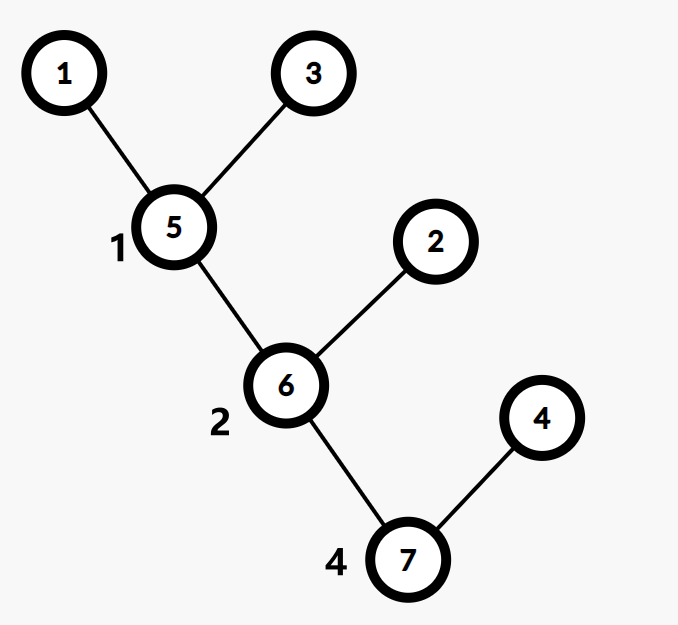
性质

• kruskal 重构树是一棵二叉堆
• 最小生成树的重构树是大根堆，最大生成树的重构树是小根堆
• 图上两点最小路径的最大值或最大路径的最小值为重构树上两点的 lca 的点权。
• 重构树上共 \(n\times 2-1\) 的点，其中，n 个叶节点为原来图中的节点。

例题讲解

归程

这个题可以用可持久化并查集切掉。

原谅我不会

海拔比水位高的路车可以通过，剩下的路只能步行涉水。

那么就先预处理出整张图的 kruskal 重构树，然后找到树上的一个节点 x，满足 val[x]>p&&val[fa[x]]<=p，这样，以 x 为根的子树中的叶节点就是能通过车连通的。

提前预处理出图上每个节点到 1 号节点的最短路，然后在重构树中维护每个节点为根时子树中距离 1 号节点的最小值。

至于怎么找到重构树上的节点 x，那就要用到倍增了。

坑点

1. 最短路用 dijkstra，因为 SPFA 死了。
2. 多测记得清空，尤其是 lastans 容易忘。

Code

#include<cstdio>
#include<cstring>
#include<queue>
#include<vector>
#include<algorithm>
using namespace std;
int re()
{
	int s=0,f=1;char ch=getchar();
	while(ch>'9'||ch<'0')
	{
		if(ch=='-')f=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9')
		s=s*10+ch-48,ch=getchar();
	return s*f;
}
void wr(int s)
{
	if(s<0)putchar('-'),s=-s;
	if(s>9)wr(s/10);
	putchar(s%10+48);
}
const int inf=4e5+7;
int t,n,m,q,k,s,last;
int fir[inf],nex[inf<<1],poi[inf<<1],val[inf<<1],cnt;
void ins(int x,int y,int z)
{
	nex[++cnt]=fir[x];
	poi[cnt]=y;
	val[cnt]=z;
	fir[x]=cnt;
}
int dis[inf];bool vis[inf];
struct dij{
	int id,dis;
	dij(int id,int dis):id(id),dis(dis){}
	bool operator <(const dij &b)const
	{
		return dis>b.dis;
	}
};
struct kruskal{
	int from,to,val;
	bool operator <(const kruskal &b)const
	{
		return val>b.val;
	}
};
int fat[inf],cntm,cntn;
int find(int x)
{
	if(x==fat[x])return fat[x];
	return fat[x]=find(fat[x]);
}
struct SR_heap{
	int lc,rc,val,minn;
	#define lc(i) T[i].lc
	#define rc(i) T[i].rc
};
SR_heap T[inf];
int fa[inf][20];
void dfs(int now,int from)
{
	fa[now][0]=from;
	if(lc(now)==0)
	{
		T[now].minn=dis[now];
		return;
	}
	dfs(lc(now),now);
	dfs(rc(now),now);
	T[now].minn=min(T[lc(now)].minn,T[rc(now)].minn);
}
int tiao(int x,int k)
{
	for(int i=19;i>=0;i--)
	{
		if(T[fa[x][i]].val<=k)continue;
		x=fa[x][i];
	}
	return x;
}
int main()
{
	t=re();
	while(t--)
	{
		cntn=n=re(),m=re();
		cnt=cntm=last=0;
		memset(fir,0,sizeof(fir));
		memset(nex,0,sizeof(nex));
		memset(poi,0,sizeof(poi));
		memset(val,0,sizeof(val));
		memset(dis,127,sizeof(dis));
		memset(vis,0,sizeof(vis));
		memset(fa,0,sizeof(fa));
		memset(T,0,sizeof(T));
		priority_queue<dij>heap;
		vector<kruskal>h;
		for(int i=1;i<=m;i++)
		{
			int u=re(),v=re(),l=re(),a=re();
			ins(u,v,l),ins(v,u,l);
			h.push_back((kruskal){u,v,a});
		}
		heap.push(dij(1,0));dis[1]=0;
		while(heap.size())
		{
			dij now=heap.top();heap.pop();
			if(vis[now.id])continue;
			vis[now.id]=1;
			for(int i=fir[now.id];i;i=nex[i])
			{
				int p=poi[i];
				if(dis[p]>dis[now.id]+val[i])
				{
					dis[p]=dis[now.id]+val[i];
					heap.push(dij(p,dis[p]));
				}
			}
		}
		for(int i=1;i<=n;i++)fat[i]=i;
		sort(h.begin(),h.end());
		int len=h.size();
		for(int i=0;i<len;i++)
		{
			int r1=find(h[i].from),r2=find(h[i].to);
			if(r1==r2)continue;
			cntm++;cntn++;
			fat[r1]=fat[r2]=fat[cntn]=cntn;
			T[cntn]=(SR_heap){r1,r2,h[i].val};
		}
		for(int i=1;i<=cntn;i++)
			fat[i]=find(i);
		dfs(fat[1],fat[1]);
		for(int j=1;j<20;j++)
			for(int i=1;i<=cntn;i++)
				fa[i][j]=fa[fa[i][j-1]][j-1];
		q=re(),k=re(),s=re();
		for(int i=1;i<=q;i++)
		{
			int v=re(),p=re();
			v=(v+k*last-1)%n+1;
			p=(p+k*last)%(s+1);
			wr(last=T[tiao(v,p)].minn);putchar('\n');
		}
	}
    return 0;
}

练习

P1967

P4197

kruskal 相关题目