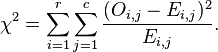spark(1.1) mllib 源码分析(一)-卡方检验

原创文章，转载请注明： 转载自http://www.cnblogs.com/tovin/p/4019131.html

在spark mllib 1.1版本中增加stat包，里面包含了一些统计相关的函数，本文主要分析其中的卡方检验的原理与实现：

一、基本原理

　　在stat包中实现了皮尔逊卡方检验，它主要包含以下两类

　　　　（1）适配度检验（Goodness of Fit test）：验证一组观察值的次数分配是否异于理论上的分配。

　　　　（2）独立性检验（independence test） ：验证从两个变量抽出的配对观察值组是否互相独立（例如：每次都从A国和B国各抽一个人，看他们的反应是否与国籍无关）

　　计算公式：

　　　　其中O表示观测值，E表示期望值

　　详细原理可以参考：http://zh.wikipedia.org/wiki/%E7%9A%AE%E7%88%BE%E6%A3%AE%E5%8D%A1%E6%96%B9%E6%AA%A2%E5%AE%9A

二、java api调用example

　　https://github.com/tovin-xu/mllib_example/blob/master/src/main/java/com/mllib/example/stat/ChiSquaredSuite.java

三、源码分析

　　1、外部api

　　　　通过Statistics类提供了4个外部接口　　

// Goodness of Fit test
def chiSqTest(observed: Vector, expected: Vector): ChiSqTestResult = {
    ChiSqTest.chiSquared(observed, expected)
  }
//Goodness of Fit test
def chiSqTest(observed: Vector): ChiSqTestResult = ChiSqTest.chiSquared(observed)

//independence test
def chiSqTest(observed: Matrix): ChiSqTestResult = ChiSqTest.chiSquaredMatrix(observed)
//independence test
def chiSqTest(data: RDD[LabeledPoint]): Array[ChiSqTestResult] = {
    ChiSqTest.chiSquaredFeatures(data)
}

　　2、Goodness of Fit test实现

　　这个比较简单，关键是根据(observed-expected)²/expected计算卡方值

 /*
   * Pearon's goodness of fit test on the input observed and expected counts/relative frequencies.
   * Uniform distribution is assumed when `expected` is not passed in.
   */
  def chiSquared(observed: Vector,
      expected: Vector = Vectors.dense(Array[Double]()),
      methodName: String = PEARSON.name): ChiSqTestResult = {

    // Validate input arguments
    val method = methodFromString(methodName)
    if (expected.size != 0 && observed.size != expected.size) {
      throw new IllegalArgumentException("observed and expected must be of the same size.")
    }
    val size = observed.size
    if (size > 1000) {
      logWarning("Chi-squared approximation may not be accurate due to low expected frequencies "
        + s" as a result of a large number of categories: $size.")
    }
    val obsArr = observed.toArray
　　// 如果expected值没有设置，默认取1.0 / size
    val expArr = if (expected.size == 0) Array.tabulate(size)(_ => 1.0 / size) else expected.toArray

　　/ 如果expected、observed值都必须要大于1
    if (!obsArr.forall(_ >= 0.0)) {
      throw new IllegalArgumentException("Negative entries disallowed in the observed vector.")
    }
    if (expected.size != 0 && ! expArr.forall(_ >= 0.0)) {
      throw new IllegalArgumentException("Negative entries disallowed in the expected vector.")
    }

    // Determine the scaling factor for expected
    val obsSum = obsArr.sum
    val expSum = if (expected.size == 0.0) 1.0 else expArr.sum
    val scale = if (math.abs(obsSum - expSum) < 1e-7) 1.0 else obsSum / expSum

    // compute chi-squared statistic
    val statistic = obsArr.zip(expArr).foldLeft(0.0) { case (stat, (obs, exp)) =>
      if (exp == 0.0) {
        if (obs == 0.0) {
          throw new IllegalArgumentException("Chi-squared statistic undefined for input vectors due"
            + " to 0.0 values in both observed and expected.")
        } else {
          return new ChiSqTestResult(0.0, size - 1, Double.PositiveInfinity, PEARSON.name,
            NullHypothesis.goodnessOfFit.toString)
        }
      }
　　// 计算(observed-expected)2/expected
      if (scale == 1.0) {
        stat + method.chiSqFunc(obs, exp)
      } else {
        stat + method.chiSqFunc(obs, exp * scale)
      }
    }
    val df = size - 1
    val pValue = chiSquareComplemented(df, statistic)
    new ChiSqTestResult(pValue, df, statistic, PEARSON.name, NullHypothesis.goodnessOfFit.toString)
  }

　　3、independence test实现

　　　　先通过下面的公式计算expected值，矩阵共有 r 行 c 列

　　　　　

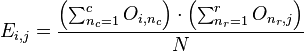
　　　　然后根据(observed-expected)²/expected计算卡方值

/*
   * Pearon's independence test on the input contingency matrix.
   * TODO: optimize for SparseMatrix when it becomes supported.
   */
  def chiSquaredMatrix(counts: Matrix, methodName:String = PEARSON.name): ChiSqTestResult = {
    val method = methodFromString(methodName)
    val numRows = counts.numRows
    val numCols = counts.numCols

    // get row and column sums
    val colSums = new Array[Double](numCols)
    val rowSums = new Array[Double](numRows)
    val colMajorArr = counts.toArray
    var i = 0
    while (i < colMajorArr.size) {
      val elem = colMajorArr(i)
      if (elem < 0.0) {
        throw new IllegalArgumentException("Contingency table cannot contain negative entries.")
      }
      colSums(i / numRows) += elem
      rowSums(i % numRows) += elem
      i += 1
    }
    val total = colSums.sum

    // second pass to collect statistic
    var statistic = 0.0
    var j = 0
    while (j < colMajorArr.size) {
      val col = j / numRows
      val colSum = colSums(col)
      if (colSum == 0.0) {
        throw new IllegalArgumentException("Chi-squared statistic undefined for input matrix due to"
          + s"0 sum in column [$col].")
      }
      val row = j % numRows
      val rowSum = rowSums(row)
      if (rowSum == 0.0) {
        throw new IllegalArgumentException("Chi-squared statistic undefined for input matrix due to"
          + s"0 sum in row [$row].")
      }
      val expected = colSum * rowSum / total
      statistic += method.chiSqFunc(colMajorArr(j), expected)
      j += 1
    }
    val df = (numCols - 1) * (numRows - 1)
    val pValue = chiSquareComplemented(df, statistic)
    new ChiSqTestResult(pValue, df, statistic, methodName, NullHypothesis.independence.toString)
  }

原创文章，转载请注明： 转载自http://www.cnblogs.com/tovin/p/4019131.html