51nod 1296 有限制的排列（DP）

　　对于一个i，如果要比邻居大，那么i比i-1大，i+1比i小，比邻居小同理。设v[i]=0表示i与i-1的关系无限制，v[i]=1表示a[i-1]>a[i]，v[i]=2表示a[i-1]<a[i]

　　则有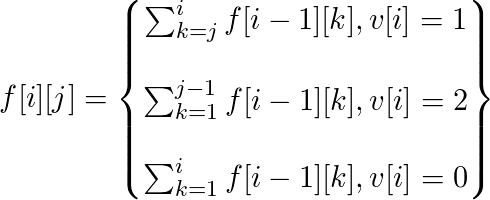

　　显然这个是可以用前缀和优化成O(N^2)的

#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#define MOD(x) (x>=mod?x-mod:x)
using namespace std;
const int maxn=,mod=1e9+;
int n,m1,m2,x,y;
int f[maxn][maxn],v[maxn];
void read(int &k)
{
    int f=;k=;char c=getchar();
    while(c<''||c>'')c=='-'&&(f=-),c=getchar();
    while(c<=''&&c>='')k=k*+c-'',c=getchar();
    k*=f;
}
int main()
{
    read(n);read(m1);read(m2);
    for(int i=;i<=m1;i++)read(x),v[x+]=,v[x+]=;
    for(int i=;i<=m2;i++)read(x),v[x+]=,v[x+]=;
    f[][]=;
    for(int i=;i<=n;i++)
    {
        if(v[i]==||!v[i])for(int j=i,sum=;j;j--)sum=MOD(sum+f[i-][j]),f[i][j]+=sum;
        if(v[i]==||!v[i])for(int j=,sum=;j<=i;j++)f[i][j]=MOD(f[i][j]+sum),sum=MOD(sum+f[i-][j]);
    }
    int ans=;
    for(int i=;i<=n;i++)ans=MOD(ans+f[n][i]);
    printf("%d\n",ans);
}