最小生成树算法详解（prim+kruskal）

最小生成树概念：

一个有 n 个结点的连通图的生成树是原图的极小连通子图，且包含原图中的所有 n 个结点，并且有保持图连通的最少的边。最小生成树可以用kruskal（克鲁斯卡尔）算法或prim（普里姆）算法求出。最小生成树其实是最小权重生成树的简称。

prim:

普里姆算法（Prim算法），图论中的一种算法，可在加权连通图里搜索最小生成树。意即由此算法搜索到的边子集所构成的树中，不但包括了连通图里的所有顶点（英语：Vertex (graph theory)），且其所有边的权值之和亦为最小。

prim算法求最小生成树的时候和边数无关，和顶点树有关，所以适合求解稠密网的最小生成树。

prim算法的步骤包括：

1. 将一个图分为两部分，一部分归为点集U，一部分归为点集V，U的初始集合为{V1}，V的初始集合为{ALL-V1}。

2. 针对U开始找U中各节点的所有关联的边的权值最小的那个，然后将关联的节点Vi加入到U中，并且从V中删除（注意不能形成环）。

3. 递归执行步骤2，直到V中的集合为空。

4. U中所有节点构成的树就是最小生成树。

实现图解：

说明	不可选	可选	已选（V_new）
此为原始的加权连通图。每条边一侧的数字代表其权值。	-	-	-
顶点D被任意选为起始点。顶点A、B、E和F通过单条边与D相连。A是距离D最近的顶点，因此将A及对应边AD以高亮表示。	C, G	A, B, E, F	D
下一个顶点为距离D或A最近的顶点。B距D为9，距A为7，E为15，F为6。因此，F距D或A最近，因此将顶点F与相应边DF以高亮表示。	C, G	B, E, F	A, D
算法继续重复上面的步骤。距离A为7的顶点B被高亮表示。	C	B, E, G	A, D, F
在当前情况下，可以在C、E与G间进行选择。C距B为8，E距B为7，G距F为11。E最近，因此将顶点E与相应边BE高亮表示。	无	C, E, G	A, D, F, B
这里，可供选择的顶点只有C和G。C距E为5，G距E为9，故选取C，并与边EC一同高亮表示。	无	C, G	A, D, F, B, E
顶点G是唯一剩下的顶点，它距F为11，距E为9，E最近，故高亮表示G及相应边EG。	无	G	A, D, F, B, E, C
现在，所有顶点均已被选取，图中绿色部分即为连通图的最小生成树。在此例中，最小生成树的权值之和为39。	无	无	A, D, F, B, E, C, G

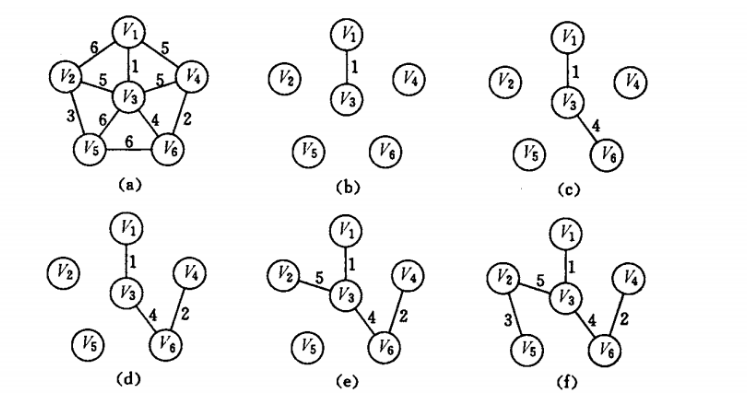
再来一张比较容易懂的图片：

(a):一个无向图，记录了各点之间的权值关系

(b):在图中选择一个与{v1}连接最小的点v3

(c):选择一个与{v1,v3}连接最小的点v6

(d):选择一个与{v1,v3,v6}连接最小的点v4

(e):选择一个与{v1,v3,v6,v4}连接最小的点v2

(f):选择一个与{v1,v3,v6,v4,v2}连接最小的点v5

生成完毕。

Kruskal算法（并查集实现）

Kruskal是一种用来寻找最小生成树的算法，在剩下的所有未选取的边中，找最小边，如果和已选取的边构成回路，则放弃，选取次小边。

实现过程

1).记Graph中有v个顶点，e个边

2).新建图Graph_new，Graph_new中拥有原图中相同的e个顶点，但没有边

3).将原图Graph中所有e个边按权值从小到大排序

4).循环：从权值最小的边开始遍历每条边直至图Graph中所有的节点都在同一个连通分量中 if 这条边连接的两个节点于图Graph_new中不在同一个连通分量中添加这条边到图Graph_new中

　　图例描述：

首先第一步，我们有一张图Graph，有若干点和边

将所有的边的长度排序，用排序的结果作为我们选择边的依据。这里再次体现了贪心算法的思想。资源排序，对局部最优的资源进行选择，排序完成后，我们率先选择了边AD。这样我们的图就变成了下图

在剩下的变中寻找。我们找到了CE。这里边的权重也是5

依次类推我们找到了6,7,7，即DF，AB，BE。

下面继续选择， BC或者EF尽管现在长度为8的边是最小的未选择的边。但是现在他们已经连通了（对于BC可以通过CE,EB来连接，类似的EF可以通过EB,BA,AD,DF来接连）。所以不需要选择他们。类似的BD也已经连通了（这里上图的连通线用红色表示了）。最后就剩下EG和FG了。当然我们选择了EG。

代码：

prim;

#include<stdio.h>
#include<string.h>
#include <iostream>
#include <bits/stdc++.h>
#define IO ios::sync_with_stdio(false);\
    cin.tie();\
    cout.tie();
#define MAX 0x3f3f3f3f
using namespace std;
];//用来标记0和1  表示这个点是否被选择过
][];//邻接矩阵用来存储图的信息
];//记录任意一点到这个点的最近距离
int n;//点个数
int prim()
{
    int i,j,now;
    ;
    /*初始化*/
    ; i<=n; i++)
    {
        dis[i]=MAX;
        logo[i]=;
    }
    /*选定1为起始点，初始化*/
    ; i<=n; i++)
    {
        dis[i]=map1[][i];
    }
    dis[]=;
    logo[]=;
    /*循环找最小边，循环n-1次*/
    ; i<n; i++)
    {
        now=MAX;
        int min1=MAX;
        ; j<=n; j++)
        {
            &&dis[j]<min1)
            {
                now=j;
                min1=dis[j];
            }
        }
        if(now==MAX)
            break;//防止不成图
        logo[now]=;
        sum+=min1;
        ; j<=n; j++)//添入新点后更新最小距离
        {
            &&dis[j]>map1[now][j])
                dis[j]=map1[now][j];
        }
    }
    if(i<n)
        printf("?\n");
    else
        printf("%d\n",sum);
}
int main()
{
    while(scanf("%d",&n),n)//n是点数
    {
        )/;//m是边数
        memset(map1,0x3f3f3f3f,sizeof(map1));//map是邻接矩阵存储图的信息
        ; i<m; i++)
        {
            int a,b,c;
            scanf("%d%d%d",&a,&b,&c);
            if(c<map1[a][b])//防止重边
                map1[a][b]=map1[b][a]=c;
        }
        prim();
    }
}

kruskal:

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
int n, m,sum;
struct node
{
    int start,end,power;//start为起始点，end为终止点，power为权值
} edge[];
];

int cmp(node a, node b)
{
    return a.power<b.power;//按照权值排序
}

int find(int x)//并查集找祖先
{
    if(x!=pre[x])
    {
        pre[x]=find(pre[x]);
    }
    return pre[x];
}

void merge(int x,int y,int n)//并查集合并函数，n是用来记录最短路中应该加入哪个点
{
    int fx=find(x);
    int fy=find(y);
    if(fx!=fy)
    {
        pre[fx]=fy;
        sum+=edge[n].power;
    }
}
int main()
{
    while(~scanf("%d", &n), n)//n是点数
    {
        sum=;
        m=n*(n-)/;//m是边数，可以输入
        int i;
        int start,end,power;
        ; i<=m; i++)
        {
            scanf("%d %d %d", &start, &end, &power);
            edge[i].start=start,edge[i].end=end,edge[i].power=power;
        }
        ; i<=m; i++)
        {
            pre[i]=i;
        }//并查集初始化
        sort(edge+, edge+m+,cmp);
        ; i <= m; i++)
        {
            merge(edge[i].start,edge[i].end,i);
        }
        printf("%d\n",sum);
    }
    ;
}