[洛谷P1941] 飞扬的小鸟

洛谷题目链接:飞扬的小鸟

题目描述

Flappy Bird是一款风靡一时的休闲手机游戏。玩家需要不断控制点击手机屏幕的频率来调节小鸟的飞行高度，让小鸟顺利通过画面右方的管道缝隙。如果小鸟一不小心撞到了水管或者掉在地上的话，便宣告失败。

为了简化问题，我们对游戏规则进行了简化和改编:

游戏界面是一个长为 \(n\)，高为 \(m\) 的二维平面，其中有 \(k\) 个管道（忽略管道的宽度）。

小鸟始终在游戏界面内移动。小鸟从游戏界面最左边任意整数高度位置出发，到达游戏界面最右边时，游戏完成。

小鸟每个单位时间沿横坐标方向右移的距离为 \(1\)，竖直移动的距离由玩家控制。如果点击屏幕，小鸟就会上升一定高度 \(X\)，每个单位时间可以点击多次，效果叠加；如果不点击屏幕，小鸟就会下降一定高度 \(Y\)。小鸟位于横坐标方向不同位置时，上升的高度 \(X\) 和下降的高度 \(Y\) 可能互不相同。

小鸟高度等于 \(0\) 或者小鸟碰到管道时，游戏失败。小鸟高度为 \(m\) 时，无法再上升。

现在,请你判断是否可以完成游戏。如果可以，输出最少点击屏幕数；否则，输出小鸟最多可以通过多少个管道缝隙。

输入输出格式

输入格式：

第 \(1\) 行有 \(3\) 个整数 \(n, m, k\)，分别表示游戏界面的长度，高度和水管的数量，每两个整数之间用一个空格隔开；

接下来的 \(n\) 行，每行 \(2\) 个用一个空格隔开的整数 \(X\) 和 \(Y\)，依次表示在横坐标位置 \(0 \sim n-1\) 上玩家点击屏幕后，小鸟在下一位置上升的高度 \(X\)，以及在这个位置上玩家不点击屏幕时，小鸟在下一位置下降的高度 \(Y\)。

接下来 \(k\) 行，每行 \(3\) 个整数 \(P, L, H\)，每两个整数之间用一个空格隔开。每行表示一个管道，其中 \(P\) 表示管道的横坐标，\(L\) 表示此管道缝隙的下边沿高度，\(H\) 表示管道缝隙上边沿的高度（输入数据保证 \(P\) 各不相同，但不保证按照大小顺序给出）。

输出格式：

共两行。

第一行，包含一个整数，如果可以成功完成游戏，则输出 \(1\)，否则输出 \(0\)。

第二行，包含一个整数，如果第一行为 \(1\)，则输出成功完成游戏需要最少点击屏幕数，否则，输出小鸟最多可以通过多少个管道缝隙。

输入输出样例

输入样例#1：

10 10 6

3 9

9 9

1 2

1 3

1 2

1 1

2 1

2 1

1 6

2 2

1 2 7

5 1 5

6 3 5

7 5 8

8 7 9

9 1 3

输出样例#1：

1

6

输入样例#2： 复制

10 10 4

1 2

3 1

2 2

1 8

1 8

3 2

2 1

2 1

2 2

1 2

1 0 2

6 7 9

9 1 4

3 8 10

输出样例#2：

0

3

说明

【输入输出样例说明】

如下图所示，蓝色直线表示小鸟的飞行轨迹，红色直线表示管道。

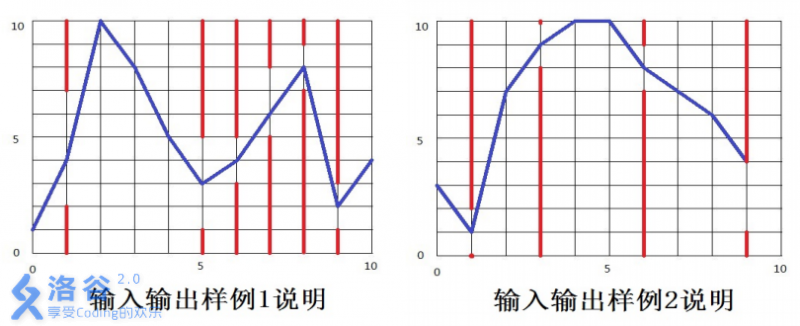
【数据范围】

对于 30%的数据：\(5 \leq n \leq 10, 5 \leq m \leq 10, k=0\)，保证存在一组最优解使得同一单位时间最多点击屏幕 \(3\)次；

对于 50%的数据：\(5 \leq n \leq 20, 5 \leq m \leq 10\)，保证存在一组最优解使得同一单位时间最多点击屏幕 \(3\) 次；

对于 70%的数据：\(5 \leq n \leq 1000, 5 \leq m \leq 100\)；

对于 100%的数据：\(5 \leq n \leq 10000\), \(5 \leq m \leq 1000\)，\(0 \leq k < n\), \(0 < X < m\), \(0 < Y < m\), \(0 < P < n\), \(0 \leq L < H \leq m\), \(L + 1 < H\)。

题意: 一个矩形中有\(k\)根管子,每次点击屏幕会上升一定高度,否则会下降一定高度.碰到管子就会游戏结束,问最少点多少下屏幕可以通过所有管道,如果无法通过所有管道,则输出\(-1\).

题解: 我们会发现到达某一个位置所需要的步数是具有最优性的,也就是说,我们可以记录下到达每个位置的最优情况,然后就自然而然的想到了DP了.

我们可以设状态\(f[i][j]\)表示到第\(i\)行第\(j\)个位置所需要的最少步数.设在\(i\)不点击屏幕会下降\(down[i]\),点击会上升\(up[i]\),那么转移就是:\(f[i+1][j] = min(f[i+1][j], min(f[i][j-up[i]+1,f[i+1][j-up[i]+1))\).

然后我们就会发现这个转移的形式是一个完全背包,也就是说,我们可以在01背包的基础上将空间的枚举按顺序枚举,这样我们的时间复杂度就是\(O(n^2)\)的了.

然后有一个小细节需要注意一下:在枚举的时候,就算当前状态是不合法的,也要先转移,因为我们在做完全背包的时候需要之前的状态转移过来.比如说现在小鸟在某个位置,然后点一次到的位置还是在管子下面,但是实际上它是可以再点几次使得小鸟通过这根管子,所以需要先给不合法的状态更新,等更新了所有状态之后再将这些不合法的状态赋回最大值.

// luogu-judger-enable-o2
#include<bits/stdc++.h>
using namespace std;
const int N = 10000+5;
const int M = 1000+5;

int n, m, k, up[N], down[N], inf, ans = 2e9, low[N], high[N], num[N];
int f[N][M];

bool access(int x){
    for(int i = 1; i <= m; i++)
        if(f[x][i] < inf) return true;
    return false;
}

int main(){
    ios::sync_with_stdio(false);
    int x, y, z; cin >> n >> m >> k;
    for(int i = 0; i < n; i++) cin >> up[i] >> down[i];
    for(int i = 1; i <= k; i++)
        cin >> x >> y >> z, low[x] = y, high[x] = z, num[x] = 1;
    for(int i = 0; i <= n; i++) num[i] += num[i-1];
    memset(f, 127/3, sizeof(f)), inf = f[0][0];
    for(int i = 1; i <= m; i++) f[0][i] = 0;
    for(int i = 0; i < n; i++){
        if(low[i+1] || high[i+1]){
            for(int j = 1; j <= m; j++){
                int nx = min(m, j+up[i]);
                if(nx < high[i+1])
                    f[i+1][nx] = min(f[i+1][nx], min(f[i][j]+1, f[i+1][j]+1));
                if(low[i+1] < j-down[i] && j-down[i] < high[i+1])
                    f[i+1][j-down[i]] = min(f[i+1][j-down[i]], f[i][j]);
            }
            for(int j = 1; j <= low[i+1]; j++)
                if(f[i+1][j] < inf)	f[i+1][j] = inf;
        } else {
            for(int j = 1; j <= m; j++){
                int nx = min(m, j+up[i]);
                f[i+1][nx] = min(f[i+1][nx], min(f[i][j]+1, f[i+1][j]+1));
                if(j > down[i])	f[i+1][j-down[i]] = min(f[i+1][j-down[i]], f[i][j]);
            }
        }
        if(!access(i+1)) cout << 0 << endl << num[i] << endl, exit(0);
    }
   	cout << 1 << endl;
    for(int i = 1; i <= m; i++) ans = min(ans, f[n][i]);
    cout << ans << endl;
    return 0;
}