【BZOJ 1095】 1095: [ZJOI2007]Hide 捉迷藏 （括号序列+线段树）

1095: [ZJOI2007]Hide 捉迷藏

Description

　　捉迷藏 Jiajia和Wind是一对恩爱的夫妻，并且他们有很多孩子。某天，Jiajia、Wind和孩子们决定在家里玩
捉迷藏游戏。他们的家很大且构造很奇特，由N个屋子和N-1条双向走廊组成，这N-1条走廊的分布使得任意两个屋
子都互相可达。游戏是这样进行的，孩子们负责躲藏，Jiajia负责找，而Wind负责操纵这N个屋子的灯。在起初的
时候，所有的灯都没有被打开。每一次，孩子们只会躲藏在没有开灯的房间中，但是为了增加刺激性，孩子们会要
求打开某个房间的电灯或者关闭某个房间的电灯。为了评估某一次游戏的复杂性，Jiajia希望知道可能的最远的两
个孩子的距离（即最远的两个关灯房间的距离）。 我们将以如下形式定义每一种操作： C(hange) i 改变第i个房
间的照明状态，若原来打开，则关闭；若原来关闭，则打开。 G(ame) 开始一次游戏，查询最远的两个关灯房间的
距离。

Input

　　第一行包含一个整数N，表示房间的个数，房间将被编号为1,2,3…N的整数。接下来N-1行每行两个整数a, b，
表示房间a与房间b之间有一条走廊相连。接下来一行包含一个整数Q，表示操作次数。接着Q行，每行一个操作，如
上文所示。

Output

　　对于每一个操作Game，输出一个非负整数到hide.out，表示最远的两个关灯房间的距离。若只有一个房间是关
着灯的，输出0；若所有房间的灯都开着，输出-1。

Sample Input

8
1 2
2 3
3 4
3 5
3 6
6 7
6 8
7
G
C 1
G
C 2
G
C 1
G

Sample Output

4
3
3
4

HINT

对于100%的数据， N ≤100000, M ≤500000。

Source

【分析】

　　此乃神题也。。今天的目标就是AC这题ORZ。。

　　跪%%%岛姐：

　　首先是括号表示法压压压：

　　比如这个图：

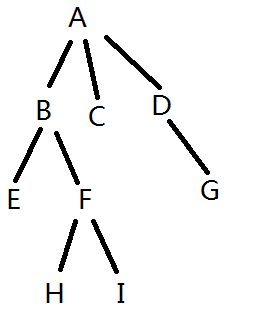　　是这样子的：[A[B[E][F[H][I]]][C][D[G]]]

　　

去掉字母后的串：[[[][[][]]][][[]]]
对于两个点PQ,他们的距离是他们之间括号序列化简之后的括号数（画个图想想就能明白，‘[’表示下去，‘]’表示上去）
那么下面的操作就能用线段树维护了。

也就是说，题目只需要动态维护：max{a+b | S’(a, b) 是 S 的一个子串，且 S’ 介于两个黑点之间}，
这里 S 是整棵树的括号编码。我们把这个量记为 dis(s)。

现在，如果可以通过左边一半的统计信息和右边一半的统计信息，得到整段编码的统计，这道题就可以用熟悉的线段树解决了。

这需要下面的分析。

考虑对于两段括号编码 S1(a1, b1) 和 S2(a2, b2)，如果它们连接起来形成 S(a, b)。

注意到 S1、S2 相连时又形成了 min{b, c} 对成对的括号，合并后它们会被抵消掉。（？..这里 b, c 应该分别是指 b1 和 a2。。。

所以：

当 a2 < b1 时第一段 [ 就被消完了，两段 ] 连在一起，例如：
] ] [ [  +  ] ] ] [ [  =  ] ] ] [ [
当 a2 >= b1 时第二段 ] 就被消完了，两段 [ 连在一起，例如：
] ] [ [ [  +  ] ] [ [  =  ] ] [ [ [ （？..反了？。。。

这样，就得到了一个十分有用的结论：

当 a2 < b1 时，(a,b) = (a1-b1+a2, b2)，
当 a2 >= b1 时，(a,b) = (a1, b1-a2+b2)。

由此，又得到几个简单的推论：

(i) a+b = a1+b2+|a2-b1| = max{(a1-b1)+(a2+b2), (a1+b1)+(b2-a2)}
(ii) a-b = a1-b1+a2-b2
(iii) b-a = b2-a2+b1-a1

由 (i) 式，可以发现，要维护 dis(s)，就必须对子串维护以下四个量：

right_plus：max{a+b | S’(a,b) 是 S 的一个后缀，且 S’ 紧接在一个黑点之后}
right_minus：max{a-b | S’(a,b) 是 S 的一个后缀，且 S’ 紧接在一个黑点之后}
left_plus：max{a+b | S’(a,b) 是 S 的一个前缀，且有一个黑点紧接在 S 之后}
left_minus：max{b-a | S’(a,b) 是 S 的一个前缀，且有一个黑点紧接在 S 之后}

这样，对于 S = S1 + S2，其中 S1(a, b)、S2(c, d)、S(e, f)，就有

(e, f) = b < c ? (a-b+c, d) : (a, b-c+d)
dis(S) = max{dis(S1), left_minus(S2)+right_plus(S1), left_plus(S2)+right_minus(S1), dis(S2)}

那么，增加这四个参数是否就够了呢？
是的，因为：

right_plus(S) = max{right_plus(S1)-c+d, right_minus(S1)+c+d, right_plus(S2)}
right_minus(S) = max{right_minus(S1)+c-d, right_minus(S2)}
left_plus(S) = max{left_plus(S2)-b+a, left_minus(S2)+b+a, left_plus(S1)}
left_minus(S) = max{left_minus(S2)+b-a, left_minus(S1)}

这样一来，就可以用线段树处理编码串了。实际实现的时候，在编码串中加进结点标号会更方便，对于底层结点，如果对应字符是一个括号或者一个白点，那 么right_plus、right_minus、left_plus、left_minus、dis 的值就都是 -maxlongint；如果对应字符是一个黑点，那么 right_plus、right_minus、left_plus、left_minus 都是 0，dis 是 -maxlongint。

现在这个题得到圆满解决，回顾这个过程，可以发现用一个串表达整棵树的信息是关键，这一“压”使得线段树这一强大工具得以利用.. .

转自：http://www.shuizilong.com/house/archives/bzoj-1095-zjoi2007hide-%E6%8D%89%E8%BF%B7%E8%97%8F/

猴赛雷啊！！！
表示即使如此，我还是纠结了好久ORZ。。
看代码吧、、

 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<iostream>
 #include<algorithm>
 using namespace std;
 #define Maxn 100010
 #define INF 0xfffffff

 int mymax(int x,int y) {return x>y?x:y;}

 int a[Maxn];
 bool c[Maxn];
 int n;

 struct node {int x,y,next;}t[*Maxn];int len=;
 int first[Maxn];

 void ins(int x,int y)
 {
     t[++len].x=x;t[len].y=y;
     t[len].next=first[x];first[x]=len;
 }

 struct nnode
 {
     int l,r,lc,rc;
     int l1,r1,l2,r2,dis,c1,c2;
 }tr[*Maxn];

 int la[Maxn],lb[Maxn],dfn[Maxn];
 int na,nb,cnt,tot;
 void dfs(int x,int f)
 {
     nb++;dfn[x]=++tot;
     la[++cnt]=na;lb[cnt]=nb;
     na=;nb=;
     for(int i=first[x];i;i=t[i].next) if(t[i].y!=f)
     {
         int y=t[i].y;
         dfs(y,x);
     }
     na++;
 }

 void upd(int x,int y)
 {
     tr[x].l1=tr[x].l2=tr[x].r1=tr[x].r2=-INF;
     tr[x].dis=-INF;
     tr[x].c1=la[y+];tr[x].c2=lb[y+];
     if(c[y+]==) tr[x].l1=la[y+]+lb[y+],tr[x].l2=lb[y+]-la[y+];
     if(c[y]==) tr[x].r1=la[y+]+lb[y+],tr[x].r2=la[y+]-lb[y+];
     if(c[y]&&c[y+]) tr[x].dis=tr[x].l1;
 }

 void merge(int x,int y,int z)
 {
     tr[z].dis=mymax(tr[x].dis,tr[y].dis);
     tr[z].dis=mymax(tr[z].dis,mymax(tr[x].r1+tr[y].l2,tr[x].r2+tr[y].l1));

     int a=tr[x].c1,b=tr[x].c2,c=tr[y].c1,d=tr[y].c2;

     if(b<c) tr[z].c1=a+c-b,tr[z].c2=d;
     else tr[z].c1=a,tr[z].c2=b+d-c;
     tr[z].l1=mymax(tr[x].l1,mymax(tr[y].l1-b+a,tr[y].l2+a+b));
     tr[z].l2=mymax(tr[x].l2,tr[y].l2+b-a);
     tr[z].r1=mymax(tr[y].r1,mymax(tr[x].r1+d-c,tr[x].r2+c+d));
     tr[z].r2=mymax(tr[y].r2,tr[x].r2+c-d);
 }

 int build(int l,int r)
 {
     int x=++tot;
     tr[x].l=l;tr[x].r=r;
     if(l==r)
     {
         upd(x,l);
     }
     else
     {
         int mid=(l+r)>>;
         tr[x].lc=build(l,mid);
         tr[x].rc=build(mid+,r);
         merge(tr[x].lc,tr[x].rc,x);
     }
     return x;
 }

 void change(int x,int y)
 {
     if(y<||y>n) return;
     if(tr[x].l==tr[x].r)
     {
         upd(x,tr[x].l);
         return;
     }
     int mid=(tr[x].l+tr[x].r)>>;
     if(y<=mid) change(tr[x].lc,y);
     else change(tr[x].rc,y);
     merge(tr[x].lc,tr[x].rc,x);
 }

 char s[];

 int main()
 {
     int bl;
     scanf("%d",&n);
     for(int i=;i<=n;i++) c[i]=;
     bl=n;
     memset(first,,sizeof(first));len=;
     for(int i=;i<n;i++)
     {
         int x,y;
         scanf("%d%d",&x,&y);
         ins(x,y);ins(y,x);
     }
     na=,nb=;cnt=;tot=;dfs(,);
     n--;
     tot=;build(,n);
     int q;
     scanf("%d",&q);
     for(int i=;i<=q;i++)
     {
         scanf("%s",s);
         if(s[]=='C')
         {
             int x;
             scanf("%d",&x);
             if(c[dfn[x]]) bl--;
             else bl++;
             c[dfn[x]]=c[dfn[x]]?:;
             change(,dfn[x]-);
             change(,dfn[x]);
         }
         else
         {
             if(bl==) printf("-1\n");
             else if(bl==) printf("0\n");
             else printf("%d\n",tr[].dis);
         }
     }
     return ;
 }

2017-01-20 09:11:16