数据结构与算法简记--Trie树

Trie树

---

概念

• 多叉树，节点为字符串中的单个字符。
• Trie 树的本质，就是利用字符串之间的公共前缀，将重复的前缀合并在一起。
• 将多个字符串按字符拆分插入Trie树，用于字符串查找，关键词提示等

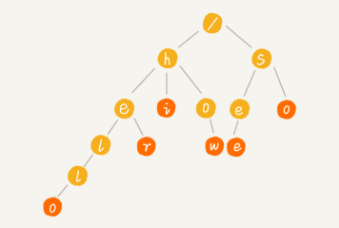
• 举例：我们有 6 个字符串，它们分别是：how，hi，her，hello，so，see。我们希望在里面多次查找某个字符串是否存在，可组成如下Trie树：

实现

• 两个操作：将字符串集合构造成 Trie 树；在Trie树中查询一个字符串
• 假设我们的字符串中只有从 a 到 z 这 26 个小写字母，我们在数组中下标为 0 的位置，存储指向子节点 a 的指针，下标为 1 的位置存储指向子节点 b 的指针，以此类推，下标为 25 的位置，存储的是指向的子节点 z 的指针。如果某个字符的子节点不存在，我们就在对应的下标的位置存储 null。

• 节点定义

class TrieNode {
  char data;
  TrieNode children[26];
}

• 构造和查询操作实现

public class Trie {
  private TrieNode root = new TrieNode('/'); // 存储无意义字符

  // 往Trie树中插入一个字符串
  public void insert(char[] text) {
    TrieNode p = root;
    for (int i = 0; i < text.length; ++i) {
      int index = text[i] - 'a';
      if (p.children[index] == null) {
        TrieNode newNode = new TrieNode(text[i]);
        p.children[index] = newNode;
      }
      p = p.children[index];
    }
    p.isEndingChar = true;
  }

  // 在Trie树中查找一个字符串
  public boolean find(char[] pattern) {
    TrieNode p = root;
    for (int i = 0; i < pattern.length; ++i) {
      int index = pattern[i] - 'a';
      if (p.children[index] == null) {
        return false; // 不存在pattern
      }
      p = p.children[index];
    }
    if (p.isEndingChar == false) return false; // 不能完全匹配，只是前缀
    else return true; // 找到pattern
  }

  public class TrieNode {
    public char data;
    public TrieNode[] children = new TrieNode[26];
    public boolean isEndingChar = false;
    public TrieNode(char data) {
      this.data = data;
    }
  }
}

• 时间复杂度：O(k), k为查询字符串的长度

Tire树很耗内存

• 每个节点需存储所有可能字符个数大小的节点数组，在包括大小写字母，数字，并且还有中文时，这个数组会很大。
• 优化方法
  • 将每个节点中的数组换成其他数据结构，来存储一个节点的子节点指针。选择有很多，比如有序数组、跳表、散列表、红黑树等。
    • 结构：假设我们用有序数组，数组中的指针按照所指向的子节点中的字符的大小顺序排列。
    • 查询：查询的时候，我们可以通过二分查找的方法，快速查找到某个字符应该匹配的子节点的指针。
    • 插入：在往 Trie 树中插入一个字符串的时候，我们为了维护数组中数据的有序性，就会稍微慢了点。
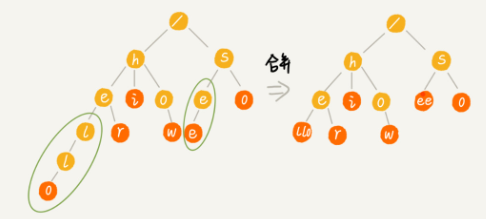
  • 缩点优化：对只有一个子节点的节点，而且此节点不是一个串的结束节点，可以将此节点与子节点合并。这样可以节省空间，但却增加了编码难度。

Trie 树与散列表、红黑树的比较

• 字符串中包含的字符集不能太大
• 要求字符串的前缀重合比较多，不然空间消耗会变大很多
• 要用 Trie 树解决问题，需要自己实现，红黑树和散列表有语言自己的成熟实现。
• 数据是指针串起来的，内存不连续，对缓存不友好。

扩展应用

• 比如输入法自动补全功能、IDE 代码编辑器自动补全功能、浏览器网址输入的自动补全功能等等。