AcWing 144. 最长异或值路径 01字典树打卡

给定一个树，树上的边都具有权值。

树中一条路径的异或长度被定义为路径上所有边的权值的异或和：

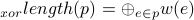
⊕ 为异或符号。

给定上述的具有n个节点的树，你能找到异或长度最大的路径吗？

输入格式

第一行包含整数n，表示树的节点数目。

接下来n-1行，每行包括三个整数u，v，w，表示节点u和节点v之间有一条边权重为w。

输出格式

输出一个整数，表示异或长度最大的路径的最大异或和。

数据范围

1≤n≤1000001≤n≤100000,
0≤u,v<n0≤u,v<n,
0≤w<2310≤w<231

输入样例：

4
0 1 3
1 2 4
1 3 6

输出样例：

7

样例解释

样例中最长异或值路径应为0->1->2,值为7 (=3 ⊕ 4)

题意：这是求任意两点之间的路径的所有值

思路：我们设置一个数组D[i]=D[father]^w[father][i]  代表根节点到当前点的异或值

然后我们任意选两点之间的路径其实也就是D[i]^D[j]，为什么呢，因为这是一棵树，我们0-x,0-y，中间有一部分路径是重复的，我们两个异或之后就会抵消掉，然后这个题就可以转换为

求最大异或对，所以我们只要最开始dfs一下，然后求最大异或对即可

#include<bits/stdc++.h>
#define maxn 100005
#define mod 1000000007
using namespace std;
typedef long long ll;
ll n,top;
ll a[maxn];
ll tree[maxn*][];
ll d[maxn];
vector<pair<ll,ll> > mp[maxn];
void insert(ll x){
    ll root=;
    for(int i=;i<;i++){
        ll z=(x>>(-i))&;
        if(!tree[root][z]) tree[root][z]=++top;
        root=tree[root][z];
    }
}
ll query(ll x){
    ll root=;
    ll sum=;
    for(int i=;i<;i++){
        ll z=(x>>(-i))&;
        if(tree[root][!z]){
            sum+=<<(-i);
            root=tree[root][!z];
        }
        else{
            root=tree[root][z];
        }
    }
    return sum;
}
void dfs(ll x,ll f){
    //cout<<x<<endl;
    for(int i=;i<mp[x].size();i++){
        pair<ll,ll> v=mp[x][i];
        if(v.first==f) continue;
        d[v.first]=d[x]^(v.second);
    //    cout<<d[v.first]<<endl;
        dfs(v.first,x);
    }
}
int main(){
    scanf("%lld",&n);
    for(int i=;i<n-;i++){
        ll u,v,z;
        scanf("%lld%lld%lld",&u,&v,&z);
        mp[u].push_back(make_pair(v,z));
        mp[v].push_back(make_pair(u,z));
    }
/*    for(int i=0;i<n;i++){
        for(int j=0;j<mp[i].size();j++){
            cout<<mp[i][j].first<<" "<<mp[i][j].second<<"      ";
        }
        cout<<"\n";
    }*/
    dfs(,-);
    /*for(int i=0;i<n;i++){
        printf("%lld ",d[i]);
    }*/
    ll mx=;
    for(int i=;i<n;i++){
        mx=max(mx,query(d[i]));
        insert(d[i]);
    }
    printf("%lld",mx);
}