CS184.1X 计算机图形学导论（第四讲）

一、齐次变换

1、平移变换

变换矩阵不能包含X,Y,Z等坐标变量

如果x坐标向右平移了5个单位长度，则x~=x+5。在变换矩阵中表示的时候添加一个w坐标变量。通过加入一个w坐标，可以实现平移变换

1>如果w>0，这表示一个真实物理世界的点，因为你可以用x,y,z三个坐标初一w得到这个真是的点。

2>如果w=0，表示一个无穷远处的点

3>在实际应用中，w等于0通常用来表示一个向量

齐次坐标的优点：只需在渲染管线的最后做一次 除法（除以w）就能将齐次坐标转换为非齐次。

一般的平移矩阵：

可以简写为2*2的矩阵，左上角是一个3*3的单位矩阵，T和0是向量，1是数值。

旋转总是相对于原点！！先做旋转再做平移，因为矩阵乘法是不可交换的

2、齐次坐标

齐次坐标的形式：简而言之，齐次坐标就是用N+1维来代表N维坐标

齐次坐标在电脑图形内无处不在，因为该坐标允许平移、旋转、缩放及透视投影等可表示为矩阵与向量相乘的一般向量运算。

我们可以在一个2D笛卡尔坐标末尾加上一个额外的变量w来形成2D齐次坐标，因此，一个点(X,Y)在齐次坐标里面变成了（x,y,w），并且有

X = x/w

Y = y/w

我们把齐次坐标转化为笛卡尔坐标的方法是前面n-1个坐标分量分别除以最后一个分量即可。

例如，笛卡尔坐标系下（1，2）的齐次坐标可以表示为（1，2，1），如果点（1，2）移动到无限远处，在笛卡尔坐标下它变为(∞,∞)，然后它的齐次坐标表示为（1，2，0），因为(1/0, 2/0) = (∞,∞)，我们可以不用”∞"来表示一个无穷远处的点了

3、旋转变换

先平移再旋转的结果：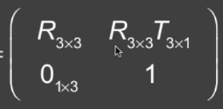

先旋转再平移的结果：

例题：

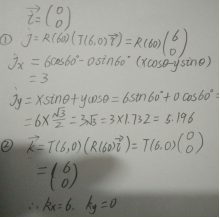
解：因为所变换的向量在后边，所以j是先平移再旋转，k是先旋转再平移，利用平移公式与旋转公式得出结果。

二、法向变换

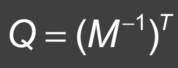
这个公式要施加到曲面上所有的法向上，产生法向变换

例题：

解：

与M相关的法向变换Q=(M^−1)^T。

对于这里的旋转矩阵 R(a⃗ ,θ), 逆矩阵等于绕着相同的旋转轴旋转 −θ:

R(a⃗ ,θ)^−1=R(a⃗ ,−θ)

对这个矩阵转置产生相似的结果:R(a⃗ ,θ)^T=R(a⃗ ,−θ)

(R(a⃗ ,θ)^T=R(a⃗,θ)^−1 是旋转矩阵的一个特殊属性。)

组织起来我们得到:

R(a⃗,θ)^−T=R(a⃗,θ)

三、旋转和坐标系

坐标系分为世界坐标系和相机坐标系

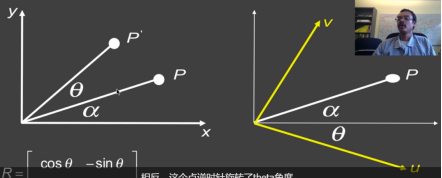
图一可看成P点逆时针旋转了θ角度，而图二可以看成坐标轴顺时针旋转了θ角度

从u,v轴分别向x,y轴画垂线，假设u,v长度为单位1，则u的坐标为（cosθ,-sinθ）,v(sinθ,cosθ),对应旋转矩阵的数值

旋转矩阵的行可以看成新坐标轴的坐标

轴角公式：

例题：

图解如下图所示：

现将标准坐标轴原点移动到新的原点处，根据新x,y画出新x,y轴的方向（也可以根据上边公式得出），i点当好在新x轴上，（根号2,0）

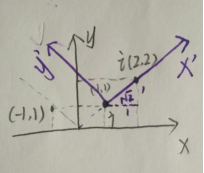
四、推导GLULOOKAT

1、定义：gluLookAt是OpenGL中观察变换的一个关键函数。

2、gluLookAt矩阵可以简要总结为:gluLookAt矩阵可以认为先将相机/视点平移到原点，然后绕着原点旋转，使得相机可以观察模型，通常，在OpenGL中相机朝着−z⃗方向观察。

在这里，平移向量就是视点坐标，更准确的说是负的视点坐标，因为不得不对世界坐标系做相反的平移