相关概念：

1.x向量和y向量

  1. import numpy as np
  2. import matplotlib.pyplot as plt
  3. x = np.array([[0,1,2,3],
  4.               [0,0,0,0],
  5.               [0,0,0,0],
  6.               [0,0,0,0]])
  7. y = np.array([[0,0,0,0],
  8.               [1,0,0,0],
  9.               [2,0,0,0],
  10.               [3,0,0,0]])
  11. plt.plot(x,y,
  12.          color = 'red',  ##全部点设置红色
  13.          marker='o',     ##形状：实心圆圈
  14.          linestyle = '') ##线性：空  点与点间不连线
  15. plt.grid(True)           ##显示网格
  16. plt.show()

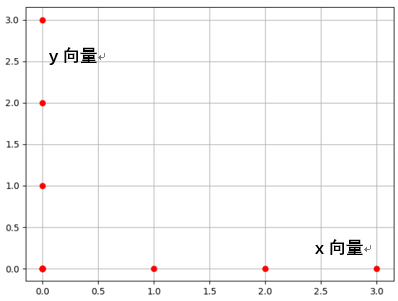
x向量和y向量

x向量：[0, 1, 2, 3]
y向量：[0, 1, 2, 3]

2.xv和yv矩阵

  1. import numpy as np
  2. import matplotlib.pyplot as plt
  3. x = [0,1,2,3]
  4. y = [0,1,2,3]
  5. print(x)
  6. print(y)
  7. x,y = np.meshgrid(x,y)
  8. print(x)
  9. print(y)
  10. plt.plot(x,y,
  11.          color = 'red',  ##全部点设置红色
  12.          marker='o',     ##形状：实心圆圈
  13.          linestyle = '') ##线性：空  点与点间不连线
  14. plt.grid(True)           ##显示网格
  15. plt.show()

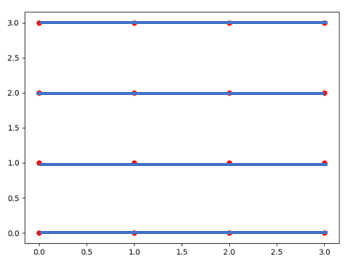
xv和yv坐标矩阵

xv坐标矩阵：

[[0 1 2 3]
 [0 1 2 3]
 [0 1 2 3]
 [0 1 2 3]]

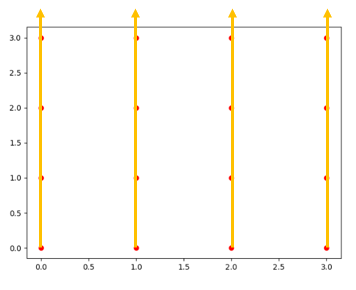
yv坐标矩阵：

[[0 0 0 0]
 [1 1 1 1]
 [2 2 2 2]
 [3 3 3 3]]

z：网格平面坐标

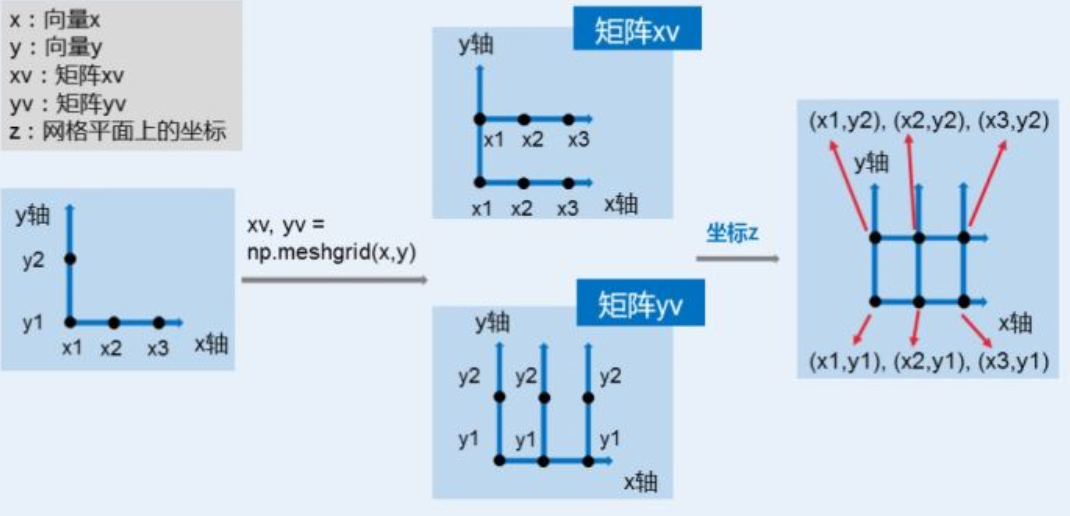
图片来源：https://www.cnblogs.com/lantingg/p/9082333.html

  1. import numpy as np
  2. import matplotlib.pyplot as plt
  3. #调用meshgrid实现以上功能
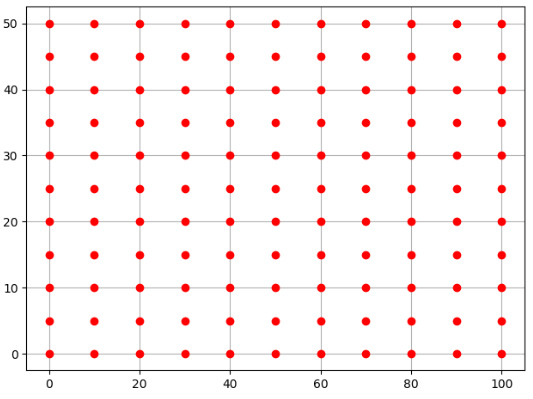
  4. x = np.linspace(0,100,11)
  5. y = np.linspace(0,50,11)
  6. print(x)
  7. print(y)
  8. x,y = np.meshgrid(x,y)
  9. print('x--meshgrid后的数据',x)
  10. print('y--meshgrid后的数据',y)
  11. plt.plot(x,y,
  12.          color = 'red',  ##全部点设置红色
  13.          marker='o',     ##形状：实心圆圈
  14.          linestyle = '') ##线性：空  点与点间不连线
  15. plt.grid(True)           ##显示网格
  16. plt.show()
  17. '''
  18. x = [  0.  10.  20.  30.  40.  50.  60.  70.  80.  90. 100.]
  19. y = [ 0.  5. 10. 15. 20. 25. 30. 35. 40. 45. 50.]
  20. x--meshgrid后的数据 [将x一维数组，重复11次]
  21. [[  0.  10.  20.  30.  40.  50.  60.  70.  80.  90. 100.]
  22.  [  0.  10.  20.  30.  40.  50.  60.  70.  80.  90. 100.]
  23.  [  0.  10.  20.  30.  40.  50.  60.  70.  80.  90. 100.]
  24.  [  0.  10.  20.  30.  40.  50.  60.  70.  80.  90. 100.]
  25.  [  0.  10.  20.  30.  40.  50.  60.  70.  80.  90. 100.]
  26.  [  0.  10.  20.  30.  40.  50.  60.  70.  80.  90. 100.]
  27.  [  0.  10.  20.  30.  40.  50.  60.  70.  80.  90. 100.]
  28.  [  0.  10.  20.  30.  40.  50.  60.  70.  80.  90. 100.]
  29.  [  0.  10.  20.  30.  40.  50.  60.  70.  80.  90. 100.]
  30.  [  0.  10.  20.  30.  40.  50.  60.  70.  80.  90. 100.]
  31.  [  0.  10.  20.  30.  40.  50.  60.  70.  80.  90. 100.]]
  32. y--meshgrid后的数据 [将y一位数组转置成列，再重复11次]
  33. [[ 0.  0.  0.  0.  0.  0.  0.  0.  0.  0.  0.]
  34.  [ 5.  5.  5.  5.  5.  5.  5.  5.  5.  5.  5.]
  35.  [10. 10. 10. 10. 10. 10. 10. 10. 10. 10. 10.]
  36.  [15. 15. 15. 15. 15. 15. 15. 15. 15. 15. 15.]
  37.  [20. 20. 20. 20. 20. 20. 20. 20. 20. 20. 20.]
  38.  [25. 25. 25. 25. 25. 25. 25. 25. 25. 25. 25.]
  39.  [30. 30. 30. 30. 30. 30. 30. 30. 30. 30. 30.]
  40.  [35. 35. 35. 35. 35. 35. 35. 35. 35. 35. 35.]
  41.  [40. 40. 40. 40. 40. 40. 40. 40. 40. 40. 40.]
  42.  [45. 45. 45. 45. 45. 45. 45. 45. 45. 45. 45.]
  43.  [50. 50. 50. 50. 50. 50. 50. 50. 50. 50. 50.]]
  44. '''

实例

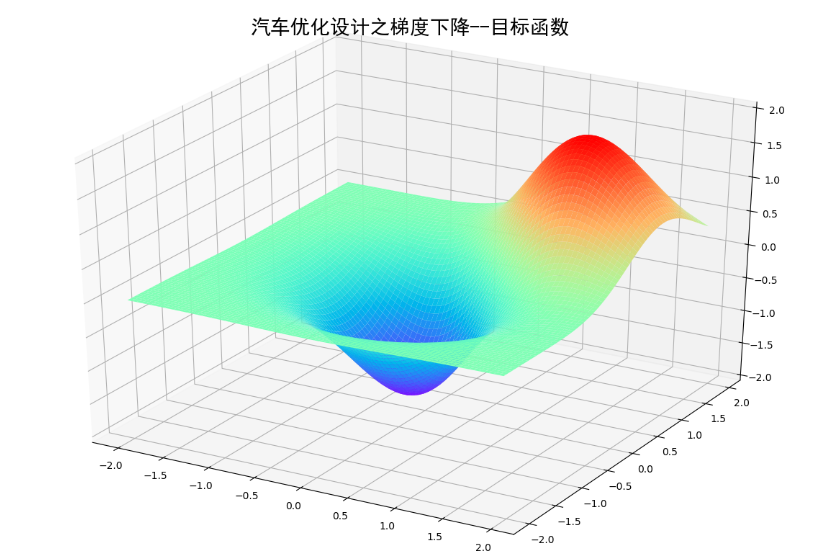
  1. import numpy as np
  2. from matplotlib import pyplot as plt
  3. from mpl_toolkits.mplot3d import  Axes3D
  4. def plot_3d():
  5.     fig = plt.figure(figsize=(12,8))
  6.     ax = Axes3D(fig)
  7.     x = np.arange(-2,2,0.05)
  8.     y = np.arange(-2,2,0.05)
  9.     ##对x,y数据执行网格化
  10.     x,y = np.meshgrid(x,y)
  11.     z1 = np.exp(-x**2-y**2)
  12.     z2 = np.exp(-(x-1)**2-(y-1)**2)
  13.     z = -(z1-z2)*2
  14.     ax.plot_surface(x,y,z,    ##x,y,z二维矩阵（坐标矩阵xv，yv,zv）
  15.                     rstride=1,##retride(row)指定行的跨度
  16.                     cstride=1,##retride(column)指定列的跨度
  17.                     cmap='rainbow')  ##设置颜色映射
  18.     ##设置z轴范围
  19.     ax.set_zlim(-2,2)
  20.     ##设置标题
  21.     plt.title('优化设计之梯度下降--目标函数',fontproperties = 'SimHei',fontsize = 20)
  22.     plt.show()
  23.     ax.plot_surface()
  24. plot_3d()

axes3d.plot_surface

 

  1. def plot_axes3d_wireframe():
  2.     fig = plt.figure(figsize=(12,8))
  3.     ax = Axes3D(fig)
  4.     x = np.arange(-2,2,0.05)
  5.     y = np.arange(-2,2,0.05)
  6.     ##对x,y数据执行网格化
  7.     x,y = np.meshgrid(x,y)
  8.     z1 = np.exp(-x**2-y**2)
  9.     z2 = np.exp(-(x-1)**2-(y-1)**2)
  10.     z = -(z1-z2)*2
  11.     ax.plot_wireframe(x,y,z,    ##x,y,z二维矩阵（坐标矩阵xv，yv,zv）
  12.                     rstride=1,##retride(row)指定行的跨度
  13.                     cstride=1,##retride(column)指定列的跨度
  14.                     cmap='rainbow')  ##设置颜色映射
  15.     ##设置z轴范围
  16.     ax.set_zlim(-2,2)
  17.     ##设置标题
  18.     plt.title('优化设计之梯度下降--目标函数',fontproperties = 'SimHei',fontsize = 20)
  19.     plt.show()
  20. plot_axes3d_wireframe()

wireframe网格图

###二维散点图

  1. ##二维散点图
  2. '''
  3. matplotlib.pyplot.scatter(x, y, s=None, c=None, marker=None, cmap=None, norm=None,
  4.                           vmin=None, vmax=None, alpha=None, linewidths=None,
  5.                           verts=None, edgecolors=None, hold=None, data=None,
  6.                           **kwargs)
  7.  
  8. x,y 平面点位置
  9. s控制节点大小
  10. c对应颜色值，c=x使点的颜色根据点的x值变化
  11. cmap：颜色映射
  12. marker：控制节点形状
  13. alpha:控制节点透明度
  14. '''
  15.  
  16. import numpy as np
  17. import matplotlib.pyplot as plt
  18.  
  19. ##二维散点图
  20. fig = plt.figure()
  21. x = np.arange(100)
  22. y = np.random.randn(100)
  23. plt.scatter(x,y,c='b')
  24. plt.scatter(x+4,y,c='b',alpha=0.5)
  25. plt.show()

二维散点图

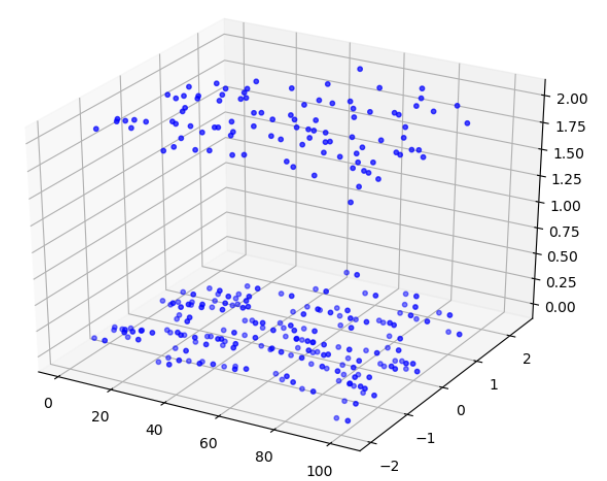
  1. ##三维散点图
    '''
    p3d.Axes3D.scatter( xs, ys, zs=0, zdir=’z’, s=20, c=None, depthshade=True, 
                       *args, **kwargs )
  2.  
  3. p3d.Axes3D.scatter3D( xs, ys, zs=0, zdir=’z’, s=20, c=None, depthshade=True,
                       *args, **kwargs)
    xs，ys 代表点x,y轴坐标
    zs代表z轴坐标：第一种，标量z=0  在空间平面z=0画图，第二种z与xs,yx同样shape的数组
    '''
  1. import numpy as np
  2. import matplotlib.pyplot as plt
  3. from mpl_toolkits.mplot3d import Axes3D
  4.  
  5. fig = plt.figure()
  6. ax  = Axes3D(fig)
  7. x = np.arange(100)
  8. y = np.random.randn(100)
  9. ax.scatter(x,y,c='b',s=10,alpha=0.5)  ##默认z=0平面
  10. ax.scatter(x+4,y,c='b',s=10,alpha=0.7)
  11. ax.scatter(x+4,y,2,c='b',s=10,alpha=0.7)  ##指定z=2平面
  12. plt.show()

z轴标量

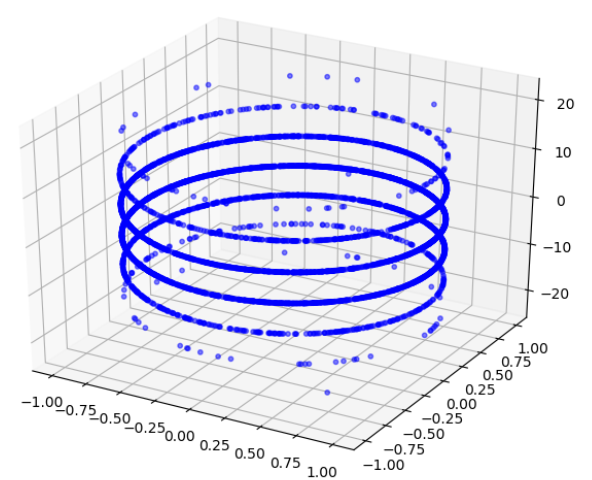
  1. import numpy as np
  2. import matplotlib.pyplot as plt
  3. from mpl_toolkits.mplot3d import Axes3D
  4.  
  5. fig = plt.figure()
  6. ax  = Axes3D(fig)
  7. z = 6*np.random.randn(5000)
  8. x = np.sin(z)
  9. y = np.cos(z)
  10. ax.scatter(x,y,z,c='b',s=10,alpha=0.5)
  11. plt.show()

z轴与x，y同样shape

  1. '''二维梯度下降法'''
  2. def func_2d_single(x,y):
  3.     '''
  4.     目标函数传入x,y
  5.     :param x,y: 自变量，一维向量
  6.     :return: 因变量，标量
  7.     '''
  8.     z1 = np.exp(-x**2-y**2)
  9.     z2 = np.exp(-(x-1)**2-(y-1)**2)
  10.     z = -(z1-2*z2)*0.5
  11.     return z
  12.  
  13. def func_2d(xy):
  14.     '''
  15.     目标函数传入xy组成的数组，如[x1,y1]
  16.     :param xy: 自变量，二维向量  （x，y）
  17.     :return: 因变量，标量
  18.     '''
  19.     z1 = np.exp(-xy[0]**2-xy[1]**2)
  20.     z2 = np.exp(-(xy[0]-1)**2-(xy[1]-1)**2)
  21.     z = -(z1-2*z2)*0.5
  22.     return z
  23. def grad_2d(xy):
  24.     '''
  25.     目标函数的梯度
  26.     :param xy: 自变量，二维向量
  27.     :return: 因变量，二维向量  (分别求偏导数，组成数组返回)
  28.     '''
  29.     grad_x = 2*xy[0]*(np.exp(-(xy[0]**2+xy[1]**2)))
  30.     grad_y = 2*xy[1]*(np.exp(-(xy[0]**2+xy[1]**2)))
  31.     return np.array([grad_x,grad_y])
  32. def gradient_descent_2d(grad, cur_xy=np.array([1, 1]), learning_rate=0.001, precision=0.001, max_iters=100000000):
  33.     '''
  34.     二维目标函数的梯度下降法
  35.     :param grad: 目标函数的梯度
  36.     :param cur_xy: 当前的x和y值
  37.     :param learning_rate: 学习率
  38.     :param precision: 收敛精度
  39.     :param max_iters: 最大迭代次数
  40.     :return: 返回极小值
  41.     '''
  42.     print(f"{cur_xy} 作为初始值开始的迭代......")
  43.     x_cur_list = []
  44.     y_cur_list = []
  45.     for i in tqdm(range(max_iters)):
  46.         grad_cur = grad(cur_xy)
  47.         ##创建两个列表，用于接收变化的x，y
  48.         x_cur_list.append(cur_xy[0])
  49.         y_cur_list.append(cur_xy[1])
  50.         if np.linalg.norm(grad_cur,ord=2)<precision:  ##求范数，ord=2 平方和开根
  51.             break    ###当梯度接近于0时，视为收敛
  52.         cur_xy = cur_xy-grad_cur*learning_rate
  53.         x_cur_list.append(cur_xy[0])
  54.         y_cur_list.append(cur_xy[1])
  55.         print('第%s次迭代：x，y = %s'%(i,cur_xy))
  56.     print('极小值 x，y = %s '%cur_xy)
  57.     return (x_cur_list,y_cur_list)
  58. if __name__=="__main__":
  59.     current_xy_list = gradient_descent_2d(grad_2d)
  60.     fig = plt.figure(figsize=(12,8))
  61.     ax = Axes3D(fig)
  62.     a = np.array(current_xy_list[0])
  63.     b = np.array(current_xy_list[1])
  64.     c = func_2d_single(a,b)
  65.     ax.scatter(a,b,c,c='Black',s=10,alpha=1,marker='o')
  66.     x = np.arange(-2,2,0.05)
  67.     y = np.arange(-2,2,0.05)
  68.     ##对x,y数据执行网格化
  69.     x,y = np.meshgrid(x,y)
  70.     z = func_2d_single(x,y)
  71.     ax.plot_surface(x,y,z,
  72.                     rstride=1,##retride(row)指定行的跨度
  73.                     cstride=1,##retride(column)指定列的跨度
  74.                     cmap='rainbow',
  75.                     alpha=0.3
  76.                     )  ##设置颜色映射
  77.     # ax.plot_wireframe(x,y,z,)
  78.     ##设置z轴范围
  79.     ax.set_zlim(-2,2)
  80.     ##设置标题
  81.     plt.title('汽车优化设计之梯度下降--二元函数',fontproperties = 'SimHei',fontsize = 20)
  82.     plt.xlabel('x',fontproperties = 'SimHei',fontsize = 20)
  83.     plt.ylabel('y', fontproperties='SimHei', fontsize=20)
  84.     plt.show()

梯度下降法及下降路径

numpy.meshgrid的理解以及3D曲面图绘制（梯度下降法实现过程）的更多相关文章

  1. python 绘图---2D、3D散点图、折线图、曲面图

    python中绘制2D曲线图需要使用到Matplotlib,Matplotlib 是一个 Python 的 2D绘图库,它以各种硬拷贝格式和跨平台的交互式环境生成出版质量级别的图形,通过 Matplo ...

  2. tecplot 把散点绘成曲面图【转载】

    转载自:http://blog.sina.com.cn/s/blog_a319f5ff0101q6s8.html 找了好久,终于自己研究出来,如何使用tecplot绘制曲面图了 第一步:数据的整理 如 ...

  3. Python的可视化包 – Matplotlib 2D图表(点图和线图,.柱状或饼状类型的图),3D图表(曲面图，散点图和柱状图)

    Python的可视化包 – Matplotlib Matplotlib是Python中最常用的可视化工具之一,可以非常方便地创建海量类型地2D图表和一些基本的3D图表.Matplotlib最早是为了可 ...

  4. numpy.meshgrid()理解

    本文的目的是记录meshgrid()的理解过程: step1. 通过一个示例引入创建网格点矩阵; step2. 基于步骤1,说明meshgrid()的作用; step3. 详细解读meshgrid() ...

  5. 对numpy.meshgrid()理解

    一句话解释numpy.meshgrid()——生成网格点坐标矩阵.关键词:网格点,坐标矩阵 网格点是什么?坐标矩阵又是什么鬼?看个图就明白了: 图中,每个交叉点都是网格点,描述这些网格点的坐标的矩阵, ...

  6. matplotlib点线 坐标刻度 3D图绘制(六)

    plot语句中支持除X,Y以外的参数,以字符串形式存在,来控制颜色.线型.点型等要素,语法形式为: plt.plot(X, Y, 'format', ...) 1 点和线的样式 颜色 参数color或 ...

  7. 【python】pandas & matplotlib 数据处理 绘制曲面图

    Python matplotlib模块,是扩展的MATLAB的一个绘图工具库,它可以绘制各种图形 建议安装 Anaconda后使用 ,集成了很多第三库,基本满足大家的需求,下载地址,对应选择pytho ...

  8. numpy.meshgrid()

    numpy提供的numpy.meshgrid()函数可以让我们快速生成坐标矩阵X,Y 语法:X,Y = numpy.meshgrid(x, y)输入:x,y,就是网格点的横纵坐标列向量(非矩阵)输出: ...

  9. numpy meshgrid 和 mgrid 的两个简单实例和解析

    numpy.meshgrid 和 numpy.mgrid 用于返回包含坐标向量的坐标矩阵. 当坐标矩阵为二维时, 可用于在图像变形时构建网格. 实例一 from __future__ import p ...

随机推荐

  1. c# winfrom程序中 enter键关联button按钮

    1,关联按钮上的Key事件             在按钮上的keypress,keydown,keyup事件必须要获得焦点,键盘上的键才能有效.        private void btnEnt ...

  2. 03机器学习实战之决策树scikit-learn实现

    sklearn.tree.DecisionTreeClassifier 基于 scikit-learn 的决策树分类模型 DecisionTreeClassifier 进行的分类运算 http://s ...

  3. 获取服务进程server.exe的pid（0号崩溃）

    #include "stdafx.h" #include <windows.h> #include <iostream> #include <COMD ...

  4. 线程工具类 - CountDownLatch(倒计时器)

    CountDownLatch官方文档 一.原理 CountDownLatch是一个非常实用的多线程控制工具类.Count Down在英文中意为倒计时,Latch意为门闩,可以简单的将CountDown ...

  5. wangeditor 支持上传视频版

    1.关于使用哪个富文本编辑器. 简单的要求,不要求发布出来的文章排版要求很高.  可用wangediter.(简单,体积小,不可修改上传图片的尺寸大小) 转载 来源: https://blog.csd ...

  6. docker中pull镜像，报错 pull access denied for ubantu, repository does not exist or may require 'docker login'

    报错说明:拒绝获取ubantu,  仓库不存在或者需要登录docker 1.先尝试注册docker 2.在拉镜像前,先登录docker, 命令:docker  login 3.然后执行 docker ...

  7. Kettle日志级别

    Kettle的日志级别LogLevel分为以下几个: Nothing 没有日志 不显示任何输出 Error 错误日志 仅仅显示错误信息 Minimal 最小日志 使用最小的日志 Basic 基本日志 ...

  8. mysql和haproxy高可用

    这片文章主要介绍mysql+haproxy+keepalived的高可用使用. 有两种模式: 第一种:数据库宕机触发VIP漂移的高可用使用. 第二种:haproxy宕机出发VIP漂移的高可用. 这两种 ...

  9. php怎么获取js的变量值

    使用php做网站的时候,经常需要我们与前端的页面进行交互,有时候我们还需要通过php来获得js变量中的值,这种情况我们可以通过在其中嵌入js代码的方式来获得这个变量. 首先我们创建一个test的php ...

  10. PHP中什么是数组

    PHP 中的数组实际上是一个有序映射.映射是一种把 values 关联到 keys 的类型. 此类型在很多方面做了优化,因此可以把它当成真正的数组,或列表(向量),散列表(是映射的一种实现),字典,集 ...