[CSP-S模拟测试]:邻面合并（状压DP）

题目背景

　　$NEWorld$作为一个$3D$游戏，对渲染（图形绘制）的效率要求极高。当玩家扩大视野范围时，可见的方块面数量将会迅速增多，以至于大量的顶点处理很快就成为了图形管线中的瓶颈。乔猫想了想，决定在大量绘制前，预处理一些相邻且有着相同材质的方块面——将许多小的面合成一个大的面，便可以在不改变渲染结果的同时减少很多顶点数量了吧......

---

题目描述

　　给定一个$N\times M$的网格，每个格子上写有$0$或$1$。现在用一些长方形覆盖其中写有$1$的格子，长方形的每条边都要与坐标轴平行。要求：每个写着$1$的格子都要被覆盖，长方形不可以重叠（重复绘制也多少会增加性能开销），也不能覆盖到任何一个写着$0$的格子（不然绘制结果就不正确了）。请问最少需要多少长方形？

---

输入格式

　　输入文件名为$merging.in$。
　　输入文件第一行两个正整数$N,M$，表示网格大小为$N$行$M$列。
　　接下来的$N$行，每行$M$个正整数$A_{ij}$（保证均为$0$或$1$），其中第$i$行$j$列的正整数表示网格$i$行$j$列里填的数。

---

样例

样例输入：

4 4
1 1 1 0
1 1 1 1
0 0 1 1
0 0 1 1

样例输出：

3

---

数据范围与提示

样例解释：

一种可行的覆盖方案（粗线表示分割线）：

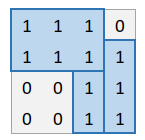
对于$30\%$的数据：$N,M\leqslant 5$。
对于$100\%$的数据：$N\leqslant 100,M\leqslant 8$。

数据范围：

对于$30\%$的数据：$N,M\leqslant 5$。
对于$100\%$的数据：$N\leqslant 100,M\leqslant 8$。

---

题解

观察$M$的范围，可以看出来应该是一个状压（当也有可能是轮廓线$DP$，甚至是插头$DP$）。

采用$8$进制压位表示每一位为起点的连续段的终点是几即可。

注意如果终点是$1$，那么起点也一定是$1$即可。

时间复杂度：$\THeta(N\times M\times 2^M)$。

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
int N,M;
int A[102][9];
bool vis[9][9];
int dp[102][150000];
vector<int> vec[102];
int ans=0x3f3f3f3f;
void dfs(int x,int y,int pre,int state)
{
	if(y>M){if(!pre)vec[x].push_back(state);return;}
	if(A[x][y])
	{
		if(!pre)
		{
			dfs(x,y+1,1,state|(1<<((y-1)<<1)));
			dfs(x,y+1,0,state|(3<<((y-1)<<1)));
		}
		else
		{
			dfs(x,y+1,1,state);
			dfs(x,y+1,0,state|(2<<((y-1)<<1)));
		}
	}
	else
	{
		if(pre)return;
		else dfs(x,y+1,0,state);
	}
}
int main()
{
	memset(dp,0x3f,sizeof(dp));
	scanf("%d%d",&N,&M);
	for(int i=1;i<=N;i++)
		for(int j=1;j<=M;j++)
			scanf("%d",&A[i][j]);
	for(int i=1;i<=N;i++)dfs(i,1,0,0);
	for(int j=0;j<vec[1].size();j++)
	{
		int state=vec[1][j],res=0;
		for(int i=1;i<=M;i++)
		{
			int flag=(state^(state>>(i<<1)<<(i<<1)))>>((i-1)<<1);
			if(flag==1||flag==3)res++;
		}
		dp[1][state]=res;
	}
	for(int i=1;i<=N;i++)
	{
		for(int j=0;j<vec[i].size();j++)
		{
			int state=vec[i][j];
			memset(vis,0,sizeof(vis));
			for(int k=1,l;k<=M;k++)
			{
				switch((state^(state>>(k<<1)<<(k<<1)))>>((k-1)<<1))
				{
					case 1:l=k;break;
					case 2:vis[l][k]=1;break;
					case 3:vis[k][k]=1;break;
				}
			}
			for(int k=0;k<vec[i+1].size();k++)
			{
				int staet=vec[i+1][k],res=0;
				for(int l=1,h;l<=M;l++)
				{
					switch((staet^(staet>>(l<<1)<<(l<<1)))>>((l-1)<<1))
					{
						case 1:h=l;break;
						case 2:res+=!vis[h][l];break;
						case 3:res+=!vis[l][l];break;
					}
				}
				dp[i+1][staet]=min(dp[i+1][staet],dp[i][state]+res);
			}
		}
	}
	for(int i=0;i<vec[N].size();i++)ans=min(ans,dp[N][vec[N][i]]);
	printf("%d",ans);
	return 0;
}

---

rp++