zoj 2112 单点修改的主席树（树状数组套主席树）

题目大意：

区间第k大问题+单点修改

基本思路：

这个题有用整体二分，cdq分治，还有主席树+平衡树的，还有就是主席树+树状数组。

我采用的是b站电子科大大佬的主席树写法，尤其喜欢他的离散化方法，所以就这么写了。

下面对代码进行下解释（当然，详细解释看注解）：

root[i]：第i棵树根节点的编号,i就是原来序列的下标，代码里从1开始

tr[i]:树状数组第i棵树根节点的编号

ur[i],ul[i]:临时用来存从第i棵树根节点编号到左右子树编号一直到底。

-----------------------------------------------------------------------------

详细注解，转自：https://blog.csdn.net/WilliamSun0122/article/details/77885781

其实静态主席树我们弄清楚之后，动态的可以很快学会。因为动态主席树就是在静态主席树的基础上增加了一批用树状数组思维维护的线段树。 
我们以下面的例子讲解。 
5 3 
3 2 1 4 7 
Q 1 4 3 询问区间[1,4]第3小数 
C 2 6 把第2个数变为6 
Q 2 5 3 询问区间[2,5]第3小数

n是原序列个数 
T[i]表示第i棵线段树的根节点编号 
S[i]表示树状数组思维建的第i棵线段树的根节点编号 
L[i]表示节点i的左子节点编号 
R[i]表示节点i的右子节点编号 
sum[i]表示节点i对应区间中数的个数。

这里离散化建树过程和静态主席树有一点不同，我们必须把所有询问先存起来并且把改变的数也加入到原序列中再离散化建树，会导致空间复杂度和静态有所区别（之前讲静态的时候提过）。所以这里我们离散化后序列为3 2 1 4 6 5分别对应原序列的3 2 1 4 7和改变后的6。

之后同静态一样建空树，按原序列前缀建树，相信不用我说了。（画图有点麻烦，我借鉴参考博客的图，这个图是没错的）

接下来就是重点了，对于题目给出的修改操作，我们新建一批线段树来记录更新，这些线段树以树状数组的思维来维护。 
一开始，S[0]、S[1]、S[2]、S[3]、S[4]、S[5] （注意一共有n+1个 即 0到n）(树状数组的每个节点)这些都与T[0]相同(也就是每个节点建了一棵空树)。 
对于C 2 6 这个操作， 我们只需要减去一个2，加上一个5（对应改变后的6）即可。 
这个更新我们按树状数组的思想更新，比如这里的减2，我们要从i=2（原序列中第2个数2在离散化后序列中的位置）即S[2]开始更新，并往上lowbit(i)直到大于5，这里我们会更新S[2]和S[4]。 
边看图边理解（这个图最后应该是在节点5那里减1）

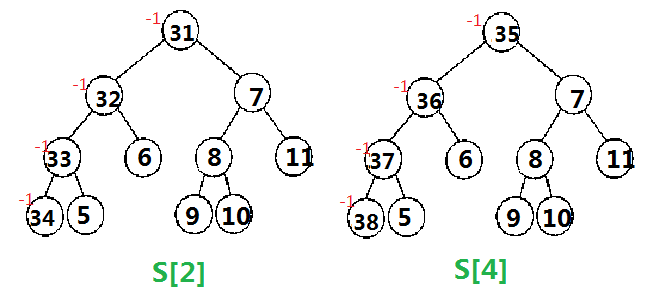
对于加5同样是从S[2]开始更新 
（这个图最后应该是在节点10那里加1）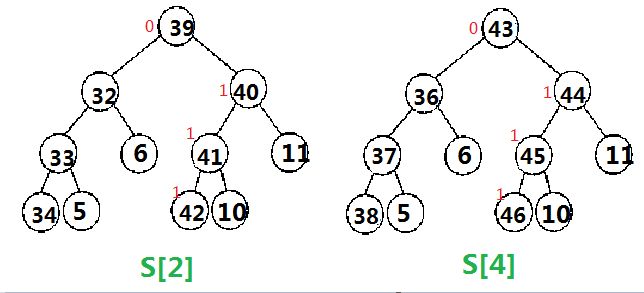 

这样我们查询的时候T[]和静态一样，再按树状数组的思维加上S[]就可算出每个节点对应区间中数的个数，再按静态的思想查询即可。

对于原序列n个数，m次询问 
空间复杂度（我的理解） 
因为这里我们要加入询问中数离散化后再建树，所以建树4*（n+m） 
按原序列更新T[]，nlog2(n+m)log2(n+m) 
每次询问更新S[]，2log2nlog2n（按树状数组最多更新的节点）log2(n+m)log2(n+m)（每次最多更新线段树中的节点） 
加起来即可，不过你真这么开数组的话肯定会MLE。

以zoj2112为例，参考博客开的范围是2*（n+m）log2(n+m)log2(n+m)（大概，我是强行解释，我范围开大会Segmentation fault，开小会RE） 
我猜大概是因为如果每次询问都是修改操作的话按静态中的开应该会是（n+m）log2(n+m)log2(n+m)还要加上一个S[]，所以要*2。

时间复杂度（我的理解） 
mlog2nlog2nlog2(n+m)

代码如下：

#include<bits/stdc++.h>

using namespace std;

typedef long long ll;

const int inf = 0x3f3f3f3f;
const int maxn = 60000+10;
int n,q,num,cnt;
int root[maxn],tr[maxn],arr[maxn],ul[maxn],ur[maxn];
vector<int>vec;
struct Node{
    int l,r,sum;
}T[maxn*32];
struct Ques{
    bool flag;
    int l,r,k;
}ques[maxn];
int getid(int x){
    return lower_bound(vec.begin(),vec.end(),x)-vec.begin()+1;
}
void update(int l,int r,int& x,int y,int pos,int val){
    T[++cnt]=T[y];
    T[cnt].sum+=val;
    x=cnt;
    if(l==r){
        return;
    }
    int mid=(l+r)/2;
    if(pos<=mid){
        update(l,mid,T[x].l,T[y].l,pos,val);
    }else{
        update(mid+1,r,T[x].r,T[y].r,pos,val);
    }
}
int lowbit(int x){
    return x&(-x);
}
void add(int x,int val){
    int ans=getid(arr[x]);
    while(x<=n){
        update(1,num,tr[x],tr[x],ans,val);
        x+=lowbit(x);
    }
}
int getSum(int x,bool flag){
    int ans=0;
    while(x>0){
        if(flag){
            ans+=T[T[ur[x]].l].sum;
        }else{
            ans+=T[T[ul[x]].l].sum;
        }
        x-=lowbit(x);
    }
    return ans;
}
int query(int l,int r,int s,int e,int ts,int te,int k){
    if(l==r){
        return l;
    }
    int mid=(l+r)/2;
    int ans=getSum(e,true)-getSum(s,false)+T[T[te].l].sum-T[T[ts].l].sum;
    if(k<=ans){
        //从根节点每次将相关所有节点下降一层
        for(int i=e;i;i-=lowbit(i)){
            ur[i]=T[ur[i]].l;
        }
        for(int i=s;i;i-=lowbit(i)){
            ul[i]=T[ul[i]].l;
        }
        return query(l,mid,s,e,T[ts].l,T[te].l,k);
    }else{
        for(int i=e;i;i-=lowbit(i)){
            ur[i]=T[ur[i]].r;
        }
        for(int i=s;i;i-=lowbit(i)){
            ul[i]=T[ul[i]].r;
        }
        return query(mid+1,r,s,e,T[ts].r,T[te].r,k-ans);
    }
}
int main(){
    int cas;
    scanf("%d",&cas);
    while(cas--){
        cnt=0;
        vec.clear();
        scanf("%d%d",&n,&q);
        for(int i=1;i<=n;i++){
            scanf("%d",&arr[i]);
            vec.push_back(arr[i]);
        }
        char op[5];
        for(int i=1;i<=q;i++){
            scanf("%s",op);
            if(op[0]=='Q'){
                ques[i].flag=false;
                scanf("%d%d%d",&ques[i].l,&ques[i].r,&ques[i].k);
            }else{
                ques[i].flag=true;
                scanf("%d%d",&ques[i].l,&ques[i].r);
                vec.push_back(ques[i].r);
            }
        }
        //离散化
        sort(vec.begin(),vec.end());
        vec.erase(unique(vec.begin(),vec.end()),vec.end());
        num=vec.size();
        for(int i=1;i<=n;i++){
            update(1,num,root[i],root[i-1],getid(arr[i]),1);
        }
        for(int i=1;i<=n;i++){
            tr[i]=root[0];
        }
        for(int i=1;i<=q;i++){
            if(ques[i].flag){
                add(ques[i].l,-1);
                arr[ques[i].l]=ques[i].r;
                add(ques[i].l,1);
            }else{
                for(int j=ques[i].r;j;j-=lowbit(j)){
                    ur[j]=tr[j];
                }
                for(int j=ques[i].l-1;j;j-=lowbit(j)){
                    ul[j]=tr[j];
                }
                printf("%d\n",vec[query(1,num,ques[i].l-1,ques[i].r,root[ques[i].l-1],root[ques[i].r],ques[i].k)-1]);
            }
        }
    }
}