T83310 【音乐会】二重变革

T83310 【音乐会】二重变革

题解

你看数据那么大，又是一道数学题

题面描述这么个代码肯定不能傻fufu的直接把代码提交上去 我批评我自己

观察代码当中有一行

也就是说明最后这个数列都将变成同一个数字，否则会一直进行下去

所以答案应该是 n*这个数字

于是乎别人惊奇的发现：

答案=这段序列所有数字的gcd * 序列长度 n

证明

咱也不知道为啥，反正它就这个样，接下来我们证明一下：

当n=2时，代码就变成：

if ( X[1]>X[2]）那么大数就变成大数减小数

（X[1] , X[2]）->（X[2] , X[1]-X[2]）

这不就是更相减损术么！！

那么我们继续把n推广到更大，那么最后每个数都变成了数列的gcd

证明

假设一开始所有数的 gcd 为 d

更相减损术无论操作多少次，这些数字的最大公因数都是不变的

最后数列里的数都变成一个数，设为k

那么此时他们的 gcd 就是 k

那么 k=d

end

PS：

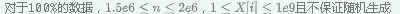
假如数据随机生成，那么这些数字的 gcd 为1的可能性极大，所以直接输出n就好

但是这道题不随机生成QWQ

代码

#include<bits/stdc++.h>

using namespace std;

int n,d=,x,y;
long long ans;

int gcd(int a,int b)
{
    if(b==) return a;
    else return gcd(b,a%b);
}

inline int read()
{
    int ans=;
    char last=' ',ch=getchar();
    while(ch<''||ch>'') last=ch,ch=getchar();
    while(ch>=''&&ch<='') ans=ans*+ch-'',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

int main()
{
    n=read();
    for(int i=;i<=n;i++)
    {
        x=read();
        d=gcd(d,x);
    }
    ans=d*n;
    printf("%ld\n",ans);

    return ;
}