CF786E ALT

题意

有一棵 \(n\) 个点的树和 \(m\) 个人，第 \(i\) 个人从 \(u_i\) 走到 \(v_i\)

现在要发宠物，要求一个人要么他自己发到宠物，要么他走的路径上的都有宠物。

求最小代价，并输出任意方案。

\(n,m \leq 20000\)

传送门

思路

对每个人和每条树边都建一个点。

源点向每个人连容量 \(1\) 的边，每条树边向汇点连容量 \(1\) 的边。每个人向他要走到的所有边连容量 \(+\infty\) 的边。

给人发就是割掉人与源的边，放边上就是割树边与汇的边，人与树边间的边不能割。当源汇不连通的时候，就是满足题意的，题目转化为最小割。

问题出在连边上，这是 \(nm\) 的，考虑如何优化连边。线段树？树上问题有点麻烦，想不到倍增。

对于一段相邻的\(2^i\)个点，都建一个点与它们所有相连，其实又有点像线段树，然后就会对于每条链得到一棵类似线段树的东西？大区间连向小区间,看起来就是。



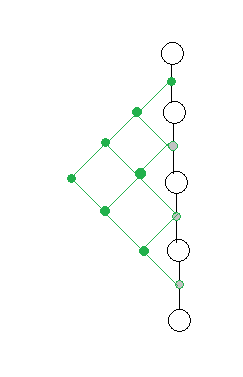
然后对每个人，将他的路径在 LCA 处分成两条路径，这两条路径分别向对应区间覆盖。

那么我们得到的新图有 \(n\log n+m\) 个点和 \(n\log n+4m\) 条边，可以通过。

这里还要输出方案。

我们知道，最小割中的边一定满流。（全局最大流，分成两个集合，其间的边一定是满流的，而也就是最小割）因此我们从源点开始 dfs，只走没满流的边，并标记被 dfs 到的点。则图被分成两部分，一部分被访问过，一部分没被访问过。其中间那些边就是一个最小割。

然后，如果一个人代表的点没被访问过，则说明他所属那条边被割了。如果一条树边代表的点被访问过，则说明它所属那条边被割了。记录标号输出

#include <bits/stdc++.h>
using std::queue;
const int W=14,N=20005*(W+1),M=N+N*4;
int to[M<<1],w[M<<1],Next[M<<1],edge,n,x,y,f[20005][W+1],idn[N],deep[N],last[N],b[20005][W+1];
int s,t,m,cnt,ans,tag[N],cur[N];
queue <int> q;
void add(int x,int y,int z){
	to[++edge]=y;
	Next[edge]=last[x];
	last[x]=edge;
	w[edge]=z;
}
void dfs(int x,int fa){
	f[x][0]=fa,deep[x]=deep[fa]+1;
	for (int i=last[x];i;i=Next[i])
		if (to[i]!=fa) {
			idn[to[i]]=(i+1)/2;
			dfs(to[i],x);
		}
}
void Add(int x,int y,int w){
	add(x,y,w);
	add(y,x,0);
}
int lca(int x,int y){
	if (deep[x]<deep[y]) std::swap(x,y);
	for (int i=W;i>=0;i--)
		if (deep[f[x][i]]>=deep[y]) x=f[x][i];
	if (x==y) return x;
	for (int i=W;i>=0;i--)
		if (f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i];
	return f[x][0];
}
void addedge(int x,int y,int id){
	for (int i=W;i>=0;i--)
		if (deep[f[x][i]]>=deep[y]){
			Add(id,b[x][i],n+1);
			x=f[x][i];
		}
}
bool bfs(){
	for (int i=0;i<=t;i++) cur[i]=last[i],deep[i]=0;
	deep[s]=1;
	q.push(s);
	while (!q.empty()){
		int x=q.front();
		q.pop();
		for (int i=last[x];i;i=Next[i])
			if (w[i] && !deep[to[i]]){
				deep[to[i]]=deep[x]+1;
				q.push(to[i]);
			}
	}
	return (deep[t]);
}
int c(int x) { return x&1?x+1:x-1; }
int dfs(int x){
	if (x==t) return 1;
	for (int i=cur[x];i;i=Next[i]){
		cur[x]=i;
		int u=to[i];
		if (deep[u]>deep[x] && w[i]){
			int di=dfs(to[i]);
			if (di){
				w[i]--;
				w[c(i)]++;
				return 1;
			}
		}
	}
	return 0;
}
void DFS(int x){
	tag[x]=1;
	for (int i=last[x];i;i=Next[i])
		if (w[i] && !tag[to[i]]) DFS(to[i]);
}
int main(){
	scanf("%d%d",&n,&m);
	for (int i=1;i<n;i++){
		scanf("%d%d",&x,&y);
		add(x,y,0),add(y,x,0);
	}
	s=0;
	dfs(1,0);
	edge=0;memset(last,0,sizeof(last));
	cnt=n;
	for (int i=2;i<=n;i++) b[i][0]=i;
	for (int i=1;i<=W;i++)
		for (int j=1;j<=n;j++)
			if (f[f[j][i-1]][i-1]){
				f[j][i]=f[f[j][i-1]][i-1];
				Add(++cnt,b[j][i-1],n+1);
				Add(cnt,b[f[j][i-1]][i-1],n+1);
				b[j][i]=cnt;
			}
	for (int i=1;i<=m;i++){
		scanf("%d%d",&x,&y);
		Add(s,++cnt,1);
		idn[cnt]=i;
		int l=lca(x,y);
		addedge(x,l,cnt),addedge(y,l,cnt);
	}
	t=cnt+1;
	for (int i=2;i<=n;i++) Add(i,t,1);
	while (bfs())
		while (dfs(s)==1) ans++;
	printf("%d\n",ans);
	DFS(s);
	ans=0;
	for (int i=last[s];i;i=Next[i])
		if (tag[to[i]]!=tag[s]) ans++;
	printf("%d ",ans);
	for (int i=last[s];i;i=Next[i])
		if (tag[to[i]]!=tag[s]) printf("%d ",idn[to[i]]);
	puts("");
	ans=0;
	for (int i=last[t];i;i=Next[i])
	if (tag[to[i]]!=tag[t]) ans++;
	printf("%d ",ans);
	for (int i=last[t];i;i=Next[i])
		if (tag[to[i]]!=tag[t]) printf("%d ",idn[to[i]]);
	return 0;
}

后记

追随神仙的脚步

抄袭于此Mrsrz