DP&图论 DAY 3 下午 考试

Problem A
Problem Description
有一天 Tarzan 写了一篇文章，我们发现这文章当中一共出现了 n 个汉字，其中第 i 个汉
字出现了 ai 次，因为 Tarzan 不希望文章被别人偷看，他要给这 n 个字分别用一个特殊的字
符串表示，其中每一个字符串由两类字符组构成，一类是 a，另一类是 ha，例如 ahaha 就是
由 a、 ha 和 ha 构成的，我们希望帮助 Tarzan 给每个汉字一个独一无二的字符串，其中不能
存在两个字符串一个是另一个的前缀。我们同时希望文章尽量短，太长会把女神惹烦，文章
长度就是每一个汉字出现次数乘以对应字符串的长度之和，请输出最短的文章长度。
Input format
第一行一个整数 n 表示汉字数量。
第二行 n 个整数，分别表示每个汉字的出现次数。
Output format
一行一个整数表示最短的文章长度。

Examples

input 1	output 1
3 2 1 1	9

input 2	output 2
4 1 2 3 4	27

Constrains and Notes
对于 15% 的数据满足： n ≤ 15
对于 40% 的数据满足： n ≤ 100
对于 70% 的数据满足： n ≤ 400
对于 100% 的数据满足： 3 ≤ n ≤ 750; 1 ≤ ai ≤ 100000，数据保证存在一定的阶梯性

Solution

每个分配一个叶子（大雾）

最深的分配给出现次数最少的

一定是二叉树，否则不优

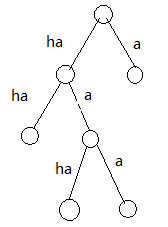
题目就是在这样一颗二叉树上选择n个没有祖先后代关系的结点（叶子结点），所需的最少层数，（ha是2层，a是1层），然后一个数组记录在最少层数的情况下文章的最小长度

为了最优，最浅的叶子要分配给出现次数最多的，最深的叶子分配给出现次数最多的

从根开始找：

dp[i][x][y][k]  当前到了第 i 层 ， i 层还有x个芽，i+1层有y个芽， 已经有k个填好了汉字，此时文章的最短长度

枚举 i 层有多少个叶子 ( 没有梦想，不想变成芽）p个

转移就是dp[i][x][y][k] = min( dp[i+1][x+y-p][x-p][k+p] + sum[n] - sum[k+p]）,

解释一下：

到了下一层i+1

i+1层的芽是x+y-p

i+1+1层的芽是x-p，因为此处我们就假设y不长了啊，然后可以变成芽的就只有x-p个

已经选好了k+p个汉字（叶子）

然后不断枚举叶子p是几个就好啦

其中sum[i]表示前 i 种汉字一共出现的次数

产生的贡献就是 k+p+1~n 这些后来的汉字提供的，因为一共n个点，选了k+p个点，已经完结了，还剩下k+p+1~n个点待处理，每个点都会经过这一层的边，所以会产生贡献

考虑优化一维度，计算每一层对答案的贡献

dp[x][y][k]  到了i层 , x本层的芽，y是下一层的芽，k是已经设置了k个叶子

dp[x][y][k] = min { dp[x+y-p][x-p][k+p] + sum[n] - sum[k+p] }

降维之后，考虑搞一搞p

我们可以一个叶子一个叶子的长，所以一次就只用考虑长一个叶子和不想长叶子两种情况

dp[x][y][k] 转移：

1.再长一个叶子  dp[x-1][y][k+1]

这里只是让x长了一个叶子，不考虑往下长芽，所以不计算代价

2.往下长芽  dp[x+y][x][k]+sum[n]-sum[k]

转移 O（1），一共有三维，所以复杂度O(n^3)

看一下zhhx的Solution：
▶ 首先我们设 dp[i][x][y][k] 表示当前到了第 i 层，这一层 x 个，
上一层 y 个，已经有 k 个结束了
▶ 转移的话就直接枚举一下， y 这一层有 p 个结束了即可，然
后算上结束的代价
▶ Time complexity O(N5) 到 O(N4 ∗ log(N))
▶ 我们考虑把第一维优化掉，我们设 dp[x][y][k] 表示最下方一
层 x 个，倒数第二层 y 个，结束了 k 个。
▶ 转移的时候就直接，枚举 y 这一层结束了 p 个，注意这里代
价不是每一个元素结束的时候记上了，我们在没往下一层
时，我们算一下这一层会产生的贡献。
▶ Time complexity O(N4)
▶ 我们再把转移优化掉。
▶ 我们就考虑每一次是把 y 减  表示，把倒数第二层一个元
素封上，还是把 y 个全部分叉转移到 dp[y][x+y][k]，加上这
一层的贡献即可。
▶ Time complexity O(N3) 滚动数组优化后 Space complexity
O(N2)

代码：

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<cmath>
#include<map>
#include<cassert>
using namespace std;
const int N=;
typedef unsigned int uint;
const uint inf=(1u<<)-;

uint n,a[N],sum[N];

bool cmp(uint x,uint y) {return x>y;}

uint dp[][N][N];int r;

int main()
{

    freopen("A.in","r",stdin);
    freopen("A.out","w",stdout);

    scanf("%u",&n);
    //assert(3<=n && n<=750);

    for (int i=;i<=n;i++) scanf("%u",&a[i]),assert(<=a[i] && a[i]<=);

    sort(a+,a+n+,cmp);
    for (int i=;i<=n;i++) sum[i]=sum[i-]+a[i];

    for (int x=;x<N;x++)
        for (int y=;y<N;y++) dp[][x][y]=dp[][x][y]=inf;

    dp[r=][][]=;
    for (int k=n-;k>=;k--)
    {
        for (int y=n-k;y>=;y--)
            for (int x=n-k-y;x>=;x--)
            dp[r^][x][y]=
            min(inf,x==&&y==?inf:
                min(
                y==?inf:dp[r][x][y-],
                x+y+y+k>n?inf:sum[n]-sum[k] + dp[r^][y][x+y]
                )
            );

    /*    for (int x=0;x<=n-(k+1);x++)
            for (int y=0;y<=n-(k+1)-x;y++) dp[r][x][y]=inf;*/
        r^=;
    }

    printf("%u\n",sum[n]+dp[r][][]);
    return ;
}

---

Problem B
Problem Description
Tarzan 现在想要知道，区间 [L,R] 内有多少数是优美的。我们定义一个数是优美的，这
个数字要满足在它 C 进制下的各位数字之和可以整除这个数字本身。 Tarzan 不会做这道题，
他希望你能帮他求出这个问题的答案。
Input format
第一行三个十进制正整数 L,R,C， L 和 R 给的是十进制形式
Output format
一行一个整数表示被认为优美的数的数量。
Examples
input 1     output 1
5 15 10    7
input 2     output 2
2 100 2    29
Constrains and Notes
对于 30% 的数据满足： R - L ≤ 100000
对于另外 10% 的数据满足： C = 2
对于另外 20% 的数据满足： C = 10
对于 100% 的数据满足： 1 ≤ L ≤ R ≤ 1018; 2 ≤ C ≤ 15

Solution

首先这道题是数位 dp 的一般的形式：求区间 [n,m] 满足某些限
制的数字的数量是多少。条件一般与数的大小无关，而与数的组
成有关。
讲什么考什么！
而同时这是一个 C 进制的数位 dp。
对于% 30 的数据直接枚举每个数判断即可。

对于 10 进制，和二进制，是 C 进制的一种特殊情况。我们可以
来考虑 C 进制怎么做。
首先限制条件和数字和是有关系的，同时还可以注意到一个数的
数字和是很小的，那么就启发我们可以枚举这个数字和 sum 是
多少，然后考虑有多少数，它的数位和是 sum，且这个数对 sum
取模为 0，也就是这个数的 sum 的倍数。

按照数位 dp 的一般套路，我们就设 f[i][sum][rest] 表示到了第 i
位，之前的数位和是 sum，数字对枚举的和取模是 rest，考虑枚
举这位是多少假设为 x，最终的和为 S：
f[i][sum][rest]+ = f[i - 1][sum + x][(rest ∗ C + x)%S]

代码：

#include<cstdio>
#include<cmath>
#include<cstdlib>
#include<algorithm>
#include<cstring>
using namespace std;
typedef long long ll;

ll A,B;
int C;
int a[],na,b[],nb,p[];

int mod;
ll f[][][];

ll query(int *a,int i,int sum,int rest,bool o)
{
    if (sum<) return ;
    if (i==) return sum==&&rest== ? :;

    if (!o&&f[i][sum][rest]!=-) return f[i][sum][rest];
    ll ans=;
    int up=o ? a[i] : C-;

    for (int j=;j<=up;j++)
    ans+=query(a,i-,sum-j,(rest+mod-j*p[i]%mod)%mod,o&&j==up);
    if (!o) f[i][sum][rest]=ans;
    return ans;
}

int main()
{
    freopen("B.in","r",stdin);
    freopen("B.out","w",stdout);
    scanf("%lld%lld%lld",&B,&A,&C);

    B--;

    while (A) a[++na]=A%C,A/=C;
    while (B) b[++nb]=B%C,B/=C;

     //printf("na=%d\n",na);
    memset(f,-,sizeof(f));

    ll ans=;
    for (int i=;i<=na*C;i++)
    {
        mod=i;
        p[]=;
        for (int j=;j<=na;j++) p[j]=p[j-]*C%mod;

        ans+=query(a,na,mod,,true)-(nb== ? :query(b,nb,mod,,true));

        for (int x=;x<=na;x++)
            for (int y=;y<=i;y++)
                for (int z=;z<=mod;z++) f[x][y][z]=-;
    }
    printf("%lld",ans);
    return ;
}

---

Problem C
Problem Description
Tarzan 非常烦数轴因为数轴上的题总是难度非常大。不过他非常喜欢线段，因为有关线
段的题总是不难，讽刺的是在一个数轴上有 n 个线段， Tarzan 希望自己喜欢的东西和讨厌的
东西不在一起，所以他要把这些线段分多次带走，每一次带走一组，最多能带走 k 次。其实
就是要把这些线段分成至多 k 组，每次带走一组，问题远没有那么简单， tarzan 还希望每次
选择的线段组都很有相似性，我们定义一组线段的相似性是组内线段交集的长度，我们现在
想知道最多分成 k 个组带走， Tarzan 最多能得到的相似性之和是多少？
Input format
第一行两个整数 n 和 k。
接下来 n 行每行两个整数 Li; Ri 表示线段的左右端点。
Output format
一行一个整数，表示最多能得到的相似性之和是多少。

Solution

% 20 和% 40 的数据
▶ 对于% 20 的数据，直接枚举每一个线段在哪一个包里面即
可。 Time complexity O(kn)
▶ 对于% 40 的数据， dfs 搜索每个线段在哪个包里面，根据写
法的优劣，可以得到最高 40 分的部分分，复杂度是和第二
类斯特林数相关。仅作了解能过即可。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<string>
#include<cstring>
#include<cstdlib>
#include<queue>

using namespace std;

inline int read()
{
    int ans=;
    char last=' ',ch=getchar();
    while(ch<''||ch>'') last=ch,ch=getchar();
    while(ch>=''&&ch<='') ans=ans*+ch-'',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

int n,k,ans=;
struct node
{
    int l,r,len;
}line[];

bool cmp(node x,node y) {return x.len >y.len ;}

int main()
{
    freopen("C.in","r",stdin);
    freopen("C.out","w",stdout);
    n=read();k=read();
    for(int i=;i<=n;i++)
    {
        line[i].l=read();
        line[i].r =read();
        line[i].len =line[i].r-line[i].l ;
    }
    sort(line+,line+n+,cmp);
    for(int i=;i<k;i++)
      ans+=line[i].len ;
    int l1 ,r1 ;
    for(int i=k;i<=n;i++)
    {
        if(i==k) l1=line[k].l ,r1=line[k].r ;
        else l1=max(l1,line[i].l),r1=min(r1,line[i].r);
    }
    if(r1-l1>) ans+=(r1-l1);
    printf("%d\n",ans);

    return ;
}

20 ’ Code

solution: % 70 的数据

观察性质！
▶ 首先最多只会有一组是空集。我们假设存在空集的话，就是
找前 K-1 长的算答案即可。再求剩余的 maxL 和 minR，即
可算出交集的大小。
▶ 假设没有空集的话。我们再观察一个性质，对于一个完全可
以包含另一个线段 B 的线段 A， A 肯定是要和 B 在一个组
的。放别的组，肯定不优。

▶ 所以我们就把所有不被任何其他线段包含的 B 线段集合拿
出来。假设有 M 个。然后这样的一组线段排序之后就是左
端点升序的同时右端点也升序了。这样的话我们选出的每一
个集合，就是连续的一段线段了。看上去就能 dp 了。
▶ 我设 dp[i][j] 前 i 个线段选了 j 个集合，首先我们这里要保证
没有空集。可得：
dp[i][j] = max(dp[x][j - 1] + R[x + 1] - L[i]jR[x + 1] > L[i])

不可能存在两个集合交集为空

如果存在一个集合交集为空，那么我们就单列出一些线段，直接取前 k-1长的线段就好

如果线段A包含B，那么A和B在一个集合结果一定不会差，因为A放到别的集合里会限制别的交集有一定限制，一定不会使得答案更优，

所以就只考虑不包含任何线段的线段，那么包含它的线段就和他放一起，答案不会更差

不包含任何线段的线段，按照左端点排个序，那么右端点也是递增的

（否则不就是包含了么）

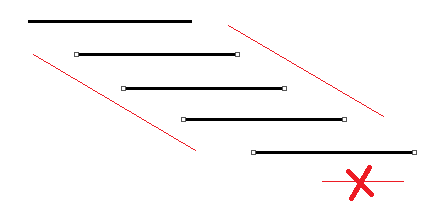
solution: % 100 的数据

dp[i][j] = max(dp[x][j - 1] + R[x + 1]jR[x + 1] > L[i]) - L[i]
这就又来到了我们的可以单调队列优化的形式了，决策点在一个
区间之内，求最小值。
求出来这个之后，我们考虑我们选了多少集合，设为 p，则这种
情况的答案为： dp[n][p]+ 其他那些不在这 m 个线段集合的线段
的前 k-p 长的线段长度之和，然后枚举 p 取最优值即可。
总复杂度 O(n ∗ k)。

代码：

#include<cstdio>
#include<cmath>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<functional>
using namespace std;
const int N=;
typedef long long ll;
const ll inf=5e13;

int n,m,k,len_n,r;

ll len[N],ans,dp[][N];
struct aa
{
    int L,R;
}t1[N],t2[N];
bool cmp(aa a,aa b)
{
    if (a.R==b.R) return a.L>b.L;
    return a.R<b.R;
}

int q[N],H,T;

int main()
{

    freopen("C.in","r",stdin);
    freopen("C.out","w",stdout);
    scanf("%d%d",&n,&k);
    for (int i=;i<=n;i++) scanf("%d%d",&t1[i].L,&t1[i].R),len[i]=t1[i].R-t1[i].L;

    sort(len+,len+n+);
    for (int i=;i<k-;i++) ans+=len[n-i];

    sort(t1+,t1+n+,cmp);

//    printf("ans=%lld\n",ans);

    memset(len,,sizeof(len));
    int mx=;
    for (int i=;i<=n;i++)
    if (t1[i].L>mx)
    {
        t2[++m]=t1[i];
        mx=t1[i].L;
    }else len[++len_n]=t1[i].R-t1[i].L;

    sort(len+,len+len_n+,greater<ll>());
    for (int i=;i<=n;i++) len[i]+=len[i-];

    sort(t2+,t2+m+,cmp);

    r=;

    for (int i=;i<=m;i++)
    if (t2[].R<=t2[i].L) dp[][i]=-inf;else dp[][i]=t2[].R-t2[i].L;

    ans=max(ans,dp[][m]+len[k-]);

    for (int j=;j<=min(k,m);j++,r^=)
    {
        q[H=T=]=;dp[r][]=-inf;
        for (int i=;i<=m;i++)
        {
            while (H<=T&&t2[q[H]+].R<=t2[i].L) H++;
            if (H<=T) dp[r][i]=dp[r^][q[H]]+t2[q[H]+].R-t2[i].L;else dp[r][i]=-inf;
            while (H<=T&&dp[r^][i]+t2[i+].R>=dp[r^][q[T]]+t2[q[T]+].R)  T--;
            q[++T]=i;
        }
        ans=max(ans,dp[r][m]+len[k-j]);
    }

    printf("%lld\n",ans);
    return ;
}

---

嘤嘤嘤wsl我太难了听不懂蒟蒻QAQ！！！