Matlab求微分方程的符号解1

一、常微分方程的求解

例1、

例2、

例3、

通常我们使用syms 和dsolve来求解；

first：

second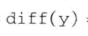：表示

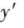
third：如果有必要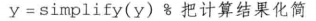

功能函数diff可以完成一元或多元函数任意阶数的微分：

（对于自变量的个数多于一个的符号矩阵，微分为Jocabian矩阵，采用功能函数Jacobian实现）

1、diff函数

diff(S,'v')：将符号“ v ”视作变量，对符号表达式或者符号矩阵求取微分。
 diff(S,n)：将S中的默认变量进行n阶微分运算，其中默认变量可用findsym函数确定。
 diff(S,'v',n)：将符号“ v ”视作变量，对符号表达式或矩阵S进行n阶微分运算。

2、jacobian函数

R=jacobian(w,v)：其中w是一个符号列向量，v是指定进行变换的变量所组成的行向量。

（第一个参数必须是列向量，第二个参数必须是行向量）

隐函数的初值问题求解：