区间第K小——可持久化线段树模板

概念

可持久化线段树又叫主席树，之所以叫主席树是因为这东西是fotile主席创建出来的。

可持久化数据结构思想，就是保留整个操作的历史，即，对一个线段树进行操作之后，保留访问操作前的线段树的能力。

最简单的方法，每操作一次，建立一颗新树。这样对空间的需求会很大。而注意到，对于点修改，每次操作最多影响 $O(\log n)$ 个节点，于是，其实操作前后的两个线段树，结构一样，因此可以共享未被影响的节点，被影响的就新建节点。于是，这样的线段树，每次操作需要O(log2(n))的空间。

线段树对于每个n的分解是唯一的，所以n相同的线段树结构相同，这也是实现可持久化线段树的基础。

分析

对于区间第K小，

先用 sort + unique 进行离散化操作；然后以离散化后的元素作为底层（接下来大概就是用线段树按顺序记录每个数字出现的次数）。

关键来了：以不同的区间建立不同的版本，及1..1为1号，1..2为2号，1..7为7号，以此类推。 查询区间 l..r 需要查询两个版本：ver[l-1]与ver[r]，同步查询两棵树，并对查询到的内容相减便是l..r中该范围内的数据(以数字出现字数为关键词)。相当于线段树的前缀和。

#include<bits/stdc++.h>
using namespace std;

const int maxn = 2e5 + ;
int n, m, size_disc;  //size_disc是离散化之后的长度
int n_init[maxn], n_disc[maxn];  //原数组   离散化后的数组
int rt[maxn], lc[maxn << ], rc[maxn << ], sum[maxn << ];  //rt:不同版本的根节点   lc/rc: 左儿子、右儿子（公用）  sum: 和（公用）
int node_cnt, pnt_disc;    //node总计数, pnt_disc: A中数字对应B中的值

void build(int& last_node, int l, int r)
{
    last_node = ++ node_cnt;
    sum[last_node] = ;
    if(l == r)  return;
    int mid = (l + r) >> ;
    build(lc[last_node], l, mid);
    build(rc[last_node], mid+, r);
}

int modify(int pre_rt, int l, int r)
{
    int new_rt = ++node_cnt;
    lc[new_rt] = lc[pre_rt];
    rc[new_rt] = rc[pre_rt];
    sum[new_rt] = sum[pre_rt] + ;

    int mid = (l + r) >> ;
    if(l == r)  return new_rt;
    if(mid >= pnt_disc)  lc[new_rt] = modify(lc[new_rt], l, mid);
    else  rc[new_rt] = modify(rc[new_rt], mid+, r);
    return new_rt;
}

int query(int rt1, int rt2, int k, int l, int r)
{
    //printf("rt1:%d  rt2:%d  k:%d  l:%d  r:%d  ", rt1, rt2, k, l, r);
    if(l == r)  return l;
    int mid = (l + r) >> ;
    int tmp = sum[lc[rt2]] - sum[lc[rt1]];
    //int tmp=sum[lc[rt2]]-sum[lc[rt1]];

    //printf("tmp:%d  k:%d\n", tmp, k);

    int ans;
    if(tmp >= k)  ans = query(lc[rt1], lc[rt2], k, l, mid);
    else ans = query(rc[rt1], rc[rt2], k-tmp, mid+, r);
    return ans;
}

void print_debug()
{
    printf("node_cnt: %d\n", node_cnt);
    for(int i = ;i <= node_cnt;i++)
        printf("%d  lc:%d  rc:%d  sum:%d\n", i, lc[i], rc[i], sum[i]);
}

int main()
{
    scanf("%d%d", &n, &m);
    for(int i = ;i <= n;i++)
    {
        scanf("%d", &n_init[i]);
        n_disc[i] = n_init[i];
    }
    sort(n_disc+, n_disc+n+);     //先排序再进行离散化
    size_disc = unique(n_disc+, n_disc+n+) - (n_disc+);

    node_cnt = ;
    build(rt[], , size_disc);
    for(int i = ;i <= n;i++)
    {
        pnt_disc = lower_bound(n_disc+, n_disc+size_disc+, n_init[i]) - n_disc;  //改了1
        rt[i] = modify(rt[i-], , size_disc);  //只在上一个版本的基础上修改
    }

    for(int i = ;i <m;i++)
    {
        int l, r, k;
        scanf("%d%d%d", &l, &r, &k);l--;
        int ans = query(rt[l], rt[r], k, , size_disc);
        printf("%d\n", n_disc[ans]);
    }
}

其中，遍历1~n建立n棵线段树的过程如下：

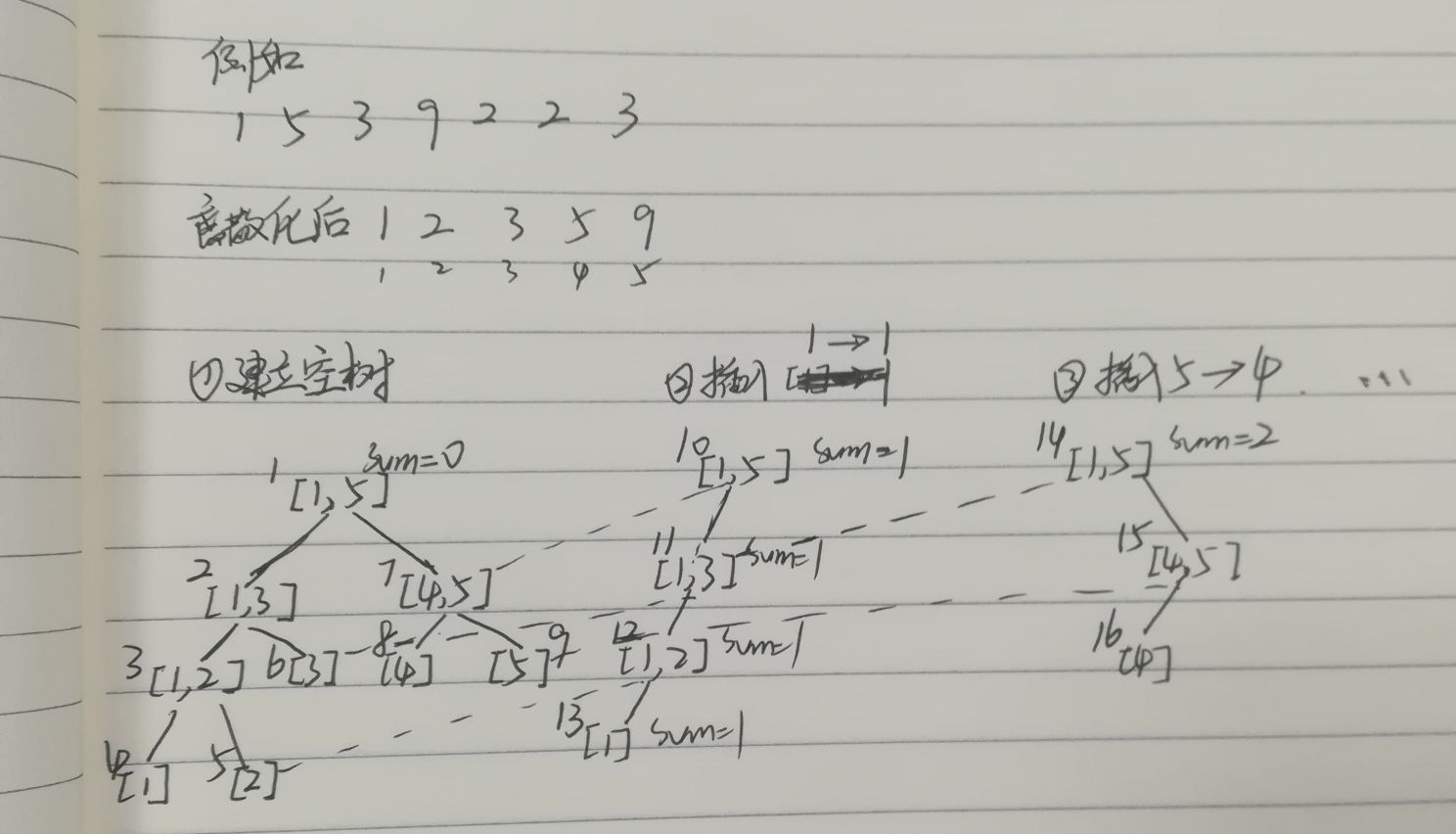
其中第i棵是建立在i-1棵的基础上，加上它们的n相同，结构也完全相同，两颗线段树相减就是这两个操作之间的变化值。

参考链接：

1. https://yfli.site/note14/

2. https://www.luogu.org/problemnew/solution/P3834