强化学习——Q-learning算法

假设有这样的房间

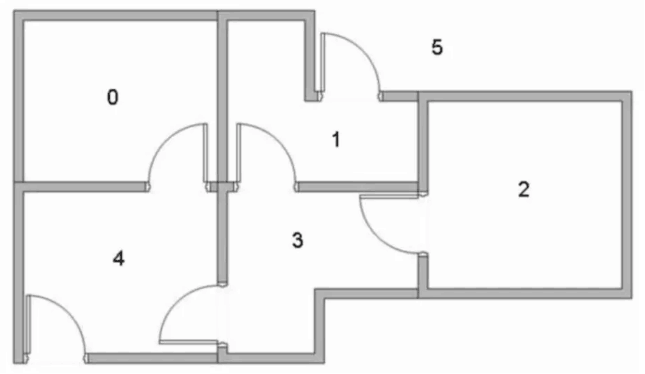
如果将房间表示成点，然后用房间之间的连通关系表示成线，如下图所示：

 

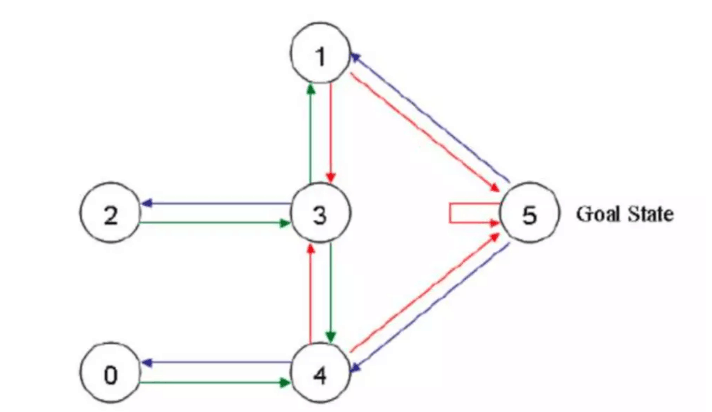
这就是房间对应的图。我们首先将agent（机器人）处于任何一个位置，让他自己走动，直到走到5房间，表示成功。为了能够走出去，我们将每个节点之间设置一定的权重，能够直接到达5的边设置为100，其他不能的设置为0，这样网络的图为：

 

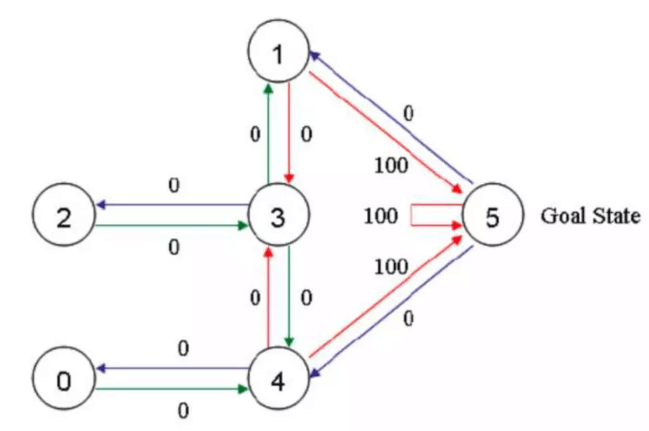
Qlearning中，最重要的就是“状态”和“动作”，状态表示处于图中的哪个节点，比如2节点，3节点等等，而动作则表示从一个节点到另一个节点的操作。

首先我们生成一个奖励矩阵矩阵，矩阵中，-1表示不可以通过，0表示可以通过，100表示直接到达终点：

同时，我们创建一个Q表，表示学习到的经验，与R表同阶，初始化为0矩阵，表示从一个state到另一个state能获得的总的奖励的折现值。

 

Q表中的值根据如下的公式来进行更新：

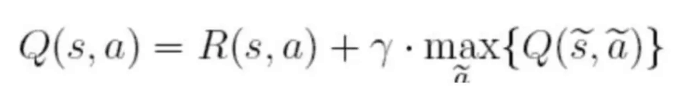
在上面的公式中，S表示当前的状态，a表示当前的动作，s_{表示下一个状态，a}表示下一个动作，λ为贪婪因子，0<λ<1,一般设置为0.8。Q表示的是，在状态s下采取动作a能够获得的期望最大收益，R是立即获得的收益，而未来一期的收益则取决于下一阶段的动作。

所以，Q-learning的学习步骤可以归结为如下：

在迭代到收敛之后，我们就可以根据Q-learning来选择我们的路径走出房间。
看一个实际的例子，首先设定λ=0.8，奖励矩阵R和Q矩阵分别初始化为：

随机选择一个状态，比如1，查看状态1所对应的R表，也就是1可以到达3或5，随机地，我们选择5，根据转移方程：

 

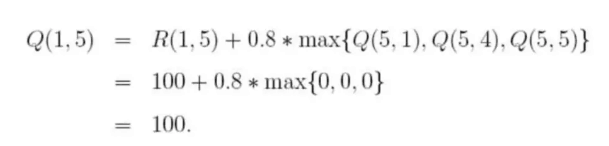
于是，Q表为：

这样，到达目标，一次尝试结束。
接下来再选择一个随机状态，比如3，3对应的下一个状态有（1，2，4都是状态3对应的非负状态），随机地，我们选择1，这样根据算法更新：

 

这样，Q表为：

经过不停的迭代，最终我们的Q表为：

 

我们不妨将Q表中的数转移到我们一开始的示意图中：

 

在得到Q表之后，我们可以根据如下的算法来选择我们的路径：

举例来说，假设我们的初始状态为2，那么根据Q表，我们选择2-3的动作，然后到达状态3之后，我们可以选择1，2，4。但是根据Q表，我们到1可以达到最大的价值，所以选择动作3-1，随后在状态1，我们按价值最大的选择选择动作1-5，所以路径为2-3-1-5.

2、代码实现

上面的例子可以用下面的代码来实现，非常的简单，直接贴上完整的代码吧：

import numpy as np
import random
r = np.array([[-1, -1, -1, -1, 0, -1], [-1, -1, -1, 0, -1, 100], [-1, -1, -1, 0, -1, -1], [-1, 0, 0, -1, 0, -1],
              [0, -1, -1, 0, -1, 100], [-1, 0, -1, -1, 0, 100]])
q = np.zeros([6,6],dtype=np.float32)
gamma = 0.8
step = 0
while step < 1000:
    state = random.randint(0,5)
    if state != 5:
        next_state_list=[]
        for i in range(6):
            if r[state,i] != -1:
                next_state_list.append(i)
        next_state = next_state_list[random.randint(0,len(next_state_list)-1)]
        qval = r[state,next_state] + gamma * max(q[next_state])
        q[state,next_state] = qval
print(q)
print(q)
# 验证
for i in range(10):
    print("第{}次验证".format(i + 1))
    state = random.randint(0, 5)
    print('机器人处于{}'.format(state))
    count = 0
    while state != 5:
        if count > 20:
            print('fail')
            break
        # 选择最大的q_max
        q_max = q[state].max()
        q_max_action = []
        for action in range(6):
            if q[state, action] == q_max:
                q_max_action.append(action)
        next_state = q_max_action[random.randint(0, len(q_max_action) - 1)]
        print("the robot goes to " + str(next_state) + '.')
        state = next_state
        count += 1

链接：https://www.jianshu.com/p/29db50000e3f