Zjoi2010排列计数Perm

这东西还是挺有思想的，道听途说一些东西，问问DuanYue同志，然后自己打表画树推了推，就搞出来了。

首先根据p i>p i/2（向下取整）这种形式，如果线段树学的好的人，一定能看出来，这是在唯一标号法标号后的形式，即父亲的权值大于两个儿子的权值，这是一个小根堆的样子。

那问题就是求给定数目的数字，求其能构成小根堆的个数。

这是一个类似树形dp的问题，我们设f[i]表示以当前节点为根所能构成小根堆的个数，那么有状态转移方程:

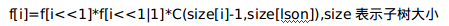
就是说当前节点及其子树一共分配了size[i]个数字，然后分给了左右子树，有上式Combine种可能，然后把左右儿子的贡献转移上来。

组合数还是老规矩打阶乘及其逆元的表，用lucas定理求一下，因为不用的话模数小的时候会崩，模数大了lucas也可以自动求组合取模。

实现过程中没有定义dp数组（其实size数组也没必要），直接带返回值的dfs搞一下。

代码略丑，勿看（主要是懒，直接define int long long 了）。

#include<iostream>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<cstdio>
#include<vector>
#include<queue>
#define int long long
using namespace std;
int n,p;
int size[];
int fac[],inv[];
int qpow(int x,int k){
    int ans=;
    for(;k;k>>=,x=1ll*x*x%p)
        if(k&) ans=1ll*ans*x%p;
    return ans;
}
void pre(){
    fac[]=;
    for(int i=;i<min(n,p);i++)
        fac[i]=1ll*fac[i-]*i%p;
    inv[min(n,p)-]=qpow(fac[min(n,p)-],p-);
    for(int i=min(n,p)-;i>=;i--)
        inv[i-]=1ll*inv[i]*i%p;
}
int com(int x,int y){
    if(y>x) return ;
    return ((1ll*fac[x]*inv[y])%p*inv[x-y]%p)%p;
}
int lucas(int x,int y){
    if(!y) return ;
    return com(x%p,y%p)*lucas(x/p,y/p)%p;
}
int dfs(int x){
    if(x>n) return ;
    size[x]++;
    int a=dfs(x<<)%p;
    int b=dfs(x<<|)%p;
    size[x]+=size[x<<]+size[x<<|];
    return 1ll*((a*b)%p*(lucas(size[x]-,size[x<<])%p))%p;
}
signed main(){
    scanf("%lld%lld",&n,&p);
    pre();
    /*for(int i=1;i<=p;i++)
        cout<<fac[i]<<" ";cout<<endl;
    for(int i=1;i<=p;i++)
        cout<<inv[i]<<" ";cout<<endl;*/
    printf("%lld",dfs()%p);
    return ;
}