2019暑期金华集训 Day1 组合计数

自闭集训 Day1

组合计数

T1

\(n\le 10\)：直接暴力枚举。

\(n\le 32\)：meet in the middle，如果左边选了\(x\)，右边选了\(y\)（且\(x+y\le B\)），那么对答案的贡献就是
\[
{B-x-y+n-1\choose n-1}
\]
根据范德蒙德恒等式
\[
{a+b\choose n} =\sum_{i=0}^n {a\choose i}{b\choose n-i}
\]
所以上面可以拆开成
\[
\sum_{i=0}^{n-1} {C-x\choose i}{-y\choose n-i-1}
\]
枚举\(x\)，关于\(y\)是一个前缀和。

AGC036 F

如果没有下界的限制，只有\(p_i\in[0,r_i]\)的限制，那么把\(r_i\)排序，方案数就是
\[
\prod (r_i-i)
\]
那么对于\(p_i\in[l_i,r_i]\)，可以发现把\(x=i,y=p_i\)的图像，必然是一个环：

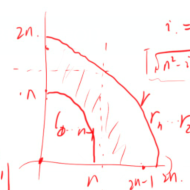
观察图像，\(r[1,n]\)是最大的，如果选了就一定在最上面，而\(l[1,n]\)和\(r[n+1,2n]\)混在一起。而且如果\(l_i>l_j\)，那么\(r_i>r_j\)。

对混在一起的东西排序。如果知道总共选了几个\(l[1,n]\)，那么当前选了之后的排名也可以求出来。

所以外层枚举选了\(k\)个\(l\)，然后内层DP：设\(dp_{i,j}\)表示前\(i\)个选了\(j\)个\(a\)的方案数。最后拿出\(dp_{2n-1,k}\)贡献答案。

不等关系

把\(>\)看做"无限制"-"<"来容斥，于是可以看做是<<?<?<<<????<?的一个串求方案数。把\(<\)看做一条边，那么就是把\(n\)个数丢进这么多个集合里，方案数就是
\[
\frac{n!}{\prod size_i!}
\]
所以可以设\(dp_i\)表示对前\(i\)个数分组，带容斥系数的方案数，于是可以枚举上一次分组的位置来转移。

使用分治FFT来转移，可以做到\(O(n\log^2 n)\)。

T4

发现如果直接算每行每列的方案数乘起来，那么会算重。

什么时候会算重呢？可以证明，只有形如

的时候会算重。

我们强制行占掉了那个交点，容斥不合法的方案，枚举有几对行列不合法，得到
\[
\sum_{i=0}^n (-1)^i {n\choose i}{m\choose i} i! (m+1)^{n-i}(n+1)^{m-i}
\]
就没了。

随机立方体

可以发现，\([0,1]\)内均匀随机与直接放\((WXH)!\)种排列是等价的。

二项式反演，转换为求\(f_k\)表示至少有\(k\)个是极大的的方案数。

先考虑二维的情况。如果一个点是极大的，那么一行一列的数都要比他小。

把极大的点拎出来，不妨设他们是从左上角往下一条对角线，并且是单调递减的。

那么对于一个不是极大的点，它的唯一限制就是小于与他同一行/列的最小的极大点。

于是可以把小于号看做一条边，矩形内的点就构成了一个森林的结构，其中右下角的点没有父亲。

根据堆的个数是\(\frac{n!}{\prod size_i}​\)的结论，可以分析出方案数就是
\[
(nm)!/(\prod_{i=1}^k (nm-(n-i)(m-i)))
\]
（大概是吧）

然后乘上一堆组合数就是答案。

拓展到三维，应该是类似的。（应该是吧）

random graph

设\(p_{n,m}\)表示\(n\)个点，随机\(m​\)条边，连通的概率。

设\(q_{n,m}=1-p_{n,m}\)。

那么答案就是\(\sum_m q_{n,m}\)。

归纳证明，可以知道\(q_{n,m}=\sum_{i=0}^{n^2} c_{n,i}(i/n^2)^m\)。

所以答案就是
\[
\sum_m \sum_{i=0}^{n^2} c_{n,i}(\frac i {n^2})^m\\
=\sum_{i=0}^{n^2} c_{n,i}\frac 1{1-\frac i {n^2}}
\]
最后用某种方式求出\(c_{n,i}\)，就做完了。

咕了

endless spin

显然\(\min-\max\)容斥，转换为每一种撒点方法的\(\frac{1}{n(n+1)-\sum s(s+1)}\)之和。

设\(dp_{i,j}\)表示前\(i\)个点，\(\sum s(s+1)=j\)，带容斥系数的方案数。

转移\(O(n)\)，总复杂度\(O(n^4)\)。

LGV lemma

对于一个有向无环图，给定\(a_{1..n}\)、\(b_{1...n}\)，求\(a_1\rightarrow b_1\)，\(a_2\rightarrow b_2\)，……的路径组，并且他们两两不想交的方案数。

设\(g_{u,v}\)表示\(a_u\rightarrow b_v\)的方案数，那么答案就是\(g\)的行列式。